Inscription / Connexion Nouveau Sujet
Vecteurs
Bonjour,
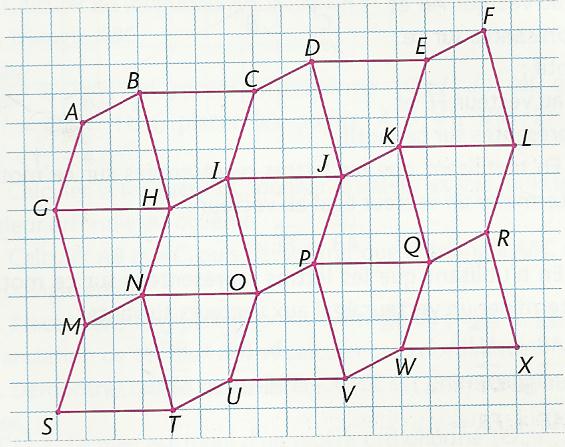
En utilisant le pavage ci-dessous réalisé à l'aide de quadrilatères identiques,répondre aux questions suivantes :
1. Quelle est l'image du quadrilatère ABHG par la translation de vecteur AJ ?
2. Quelle est l'image du quadrilatère ABHG par la symétrie ayant pour centre le milieu de [HI] ?
3. Parmi les vecteurs suivants : VB, HV, QC, PI et PH, quel est le vecteur de la translation qui transforme le
quadrilatère PQWV en BCIH ?
4. On fait agir sur le quadrilatère ABHG la translation de
vecteur GN, puis la translation de vecteur OJ.
a. Quel est le quadrilatère ainsi obtenu ?
b. Compléter l'égalité suivante :
vecteur G... = vecteur GN + vecteur OJ.
Ma difficultés est que je n'ai vraiment rien compris aux vecteurs ! Je pense avoir trouvé la première question, j'ai trouver que l'image du quadrilatère ABHG et le quadrilatère JKPQ.
Voilà
Bonjour,
très bien pour le 1 . Tu sais donc ce que c'est qu'une translation . Tout se déplace d'une même quantité dans le même sens . La quantité du déplacement et le sens sont donnés par un vecteur . C'est tout .
Pour le 2 , il faut que tu apprennes ce que c'est qu'une symétrie par rapport à un point .c'est tout .
La question 3 est l'inverse de la 1 .
Dans la question 4 on enchaîne 2 mouvements (2 translations) donc comme tu as fait le 1 , il n'y a aucune difficulté supplémentaire pour le 4 .
Et pour terminer revoir le cours sur la somme de 2 vecteurs .
Bonjour ,
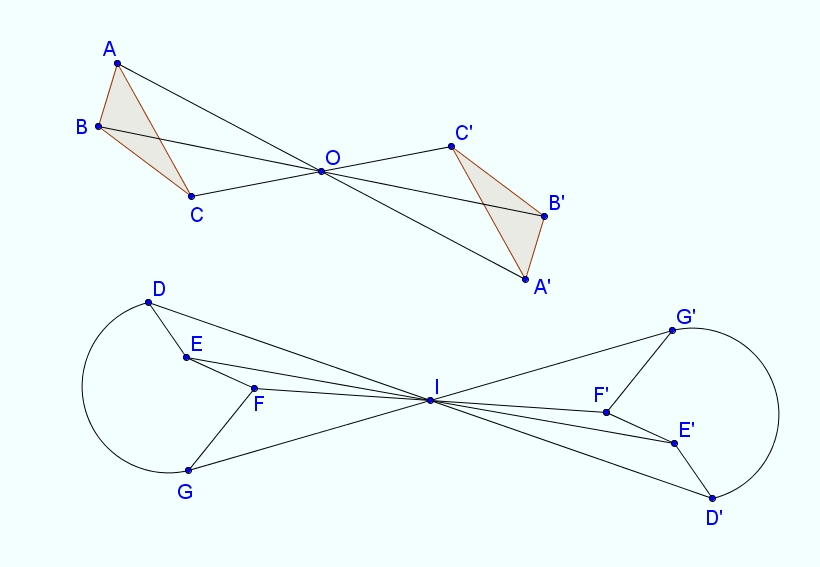
2- As-tu compris ce qu'on appelle une symétrie par rapport à un point qu'on appelle centre de symétrie ?
Je te donne 2 exemples simples . Cela devrait t'aider pour la question 2 qui est aussi facile que la 1 .
Il existe plusieurs types de transformations : translation , rotation , symétrie , ... , zoom ... Dans toutes ces transformations , on part d'une figure (ou une partie de figure) pour en obtenir une autre . C'est pas plus compliqué que cela .
Bonjour , j'ai aussi le même exercice à faire , je voulais savoir comment trouver l'image du quadrilatère ABHG par la translation de vecteur AJ ?
Bonjour ,
il suffit que tu appliques la translation à chaque sommet du quadrilatère initial (ABHG) pour obtenir les sommets du quadrilatère image .
Dans une translation , tous les points se déplacent dans une même direction et d'une même quantité . La direction et la quantité sont donnés par un vecteur . Je te donne un exemple .
Cordialement
Bonjour , j'ai un autre exercice , je l'ai fait et j'aimerai être corrigé car je ne suis pas sûre de mes réponses . Voici l'exercice :
Soit un quadrilatère MNOP .
Simplifier les sommes :
a) vecteur MN +vecteur NO
b) vecteur MO +vecteur PM
c)vecteur MN+vecteur OP - vecteur ON
2) établir la relation :
Vecteur MN + vecteur PO -vecteur PN -vecteur MO = vecteur nul
3) On suppose de plus que, Pour tout point A du plan , on a :
Vecteur AM + vecteur AN -vecteur AO -vecteur AP =vecteur nul
a) montrer que vecteur PM+vecteur ON =vecteur nul
b) que peut-on en déduire pour le quadrilatère MONP ?
Voici mes réponses :
1)a) vecteur MN+vecteur NO = vecteur MO
b) vecteur MO +vecteur PM = vecteur PO
c) vecteur MN + vecteur OP -vecteur ON = vecteur MP
2) je ne trouve pas du tout !
3)a) Vecteur AM +vecteur AN -vecteur AO -vecteur AP =vecteur nul
Vecteur AM +vecteur AN +vecteur OA +vecteur PA = vecteur nul
Vecteur PM +vecteur ON = vecteur nul
b) On peut en déduire que le quadrilatère MONP est un parallélogramme .
Merci d'avance
Bonjour ,
1-a , b et c corrects
2- Il te faut remarquer que MN - PN = MN + NP = MP
En faisant pareil avec PO et OM tu vas avoir la réponse . Je n'ai pas mis les vecteurs pour simplifier .
3 Correct
Cordialement
Oui c'est cela .
Mais tu peux t'arrêter à MP+PM=0
Il y a une petite erreur d'inattention sur ta dernière ligne C'est MP = MP
Cordialement
Bonsoir , j'ai exactement le même devoir sur les vecteur et pour la question
3.J'ai mis le vecteur PI est-ce que c'est correct ?
et pour la question 4. a) GB= GN+OJ
Merci d'avance



