Inscription / Connexion Nouveau Sujet
A la maniére d archiméde
Problème de trigo ! un horreur je ne comprend pas !!
unité en degré.
On sait que la circonférence d un cercle de rayon 1 vaut 2 .
.
On aimerai déterminer les 1er décimal de  en déterminant une valeur approché de ce périmètre.
en déterminant une valeur approché de ce périmètre.
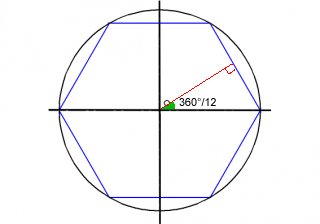
L'idée est d approximer le périmètre du cercle par le périmètre d'un polygone inscrit dans ce cercle, ici un hexagone.

1 démontrer que la longueur d un coté de l hexagone vaut 2 sin (360/12)
2 En déduire le périmètre p de l hexagone puis son demi périmètre
3 Donné une valeur approchée a 10 -3 du nombre  = |
= | -p/2|
-p/2|
A quoi correspond  ?
?
4 Démontrer que le demi périmètre d un polygone régulier a n cotés inscrit dans le même cercle vaut
n sin (360/2n)
5 Déterminer à l'aide de un= nsin (360/2n) la quatrième décimal de 
conseil : il ne faut pas avoir peur de prendre des grande valeurs de n pour que les 1 er décimal se stabilisent; vous expliquerez vos choix).
6 Pourquoi avoir utilisé les degres ° dans cette exercice
Merci de vote aide
ps je demande pas a ce qu'on me mache le travail je voudrai des indices, des pistes ...
quel est le lien avec 2sin (360/12) (360/12 = 30°= /3rad = angle en vert)
/3rad = angle en vert)
mais je ne comprend pas le rapport ...?
on a un triangle rectangle:
l'hypoténuse c'est le rayon = 1
et un angle (en vert) = 360/12 = 30°
et son sinus c'est côté opposé/hypoténuse
c est se qu il faut que je trouve
360 parce ques c'est l angle total au centre.
12 parce que chaqu'un des 6 cotés et divisé par 2.
sin = 30 / 6 ? est ça ?
360° c'est le tour complet
pour un hexagone régulier (6 côtés) on divise par 6
et pour un demi-côté on divise par 12
sinus (360°/12) = demi-côté / 1
donc la réponse a la 1 er question serai:
* Sinus car c est le moyen de trouvé la longueur du coté opposé a l angle de centre O.
* 360 ° car cest la somme de tout les angles de centre O.
* 12 car l'hexagone compte 12 triangle rectangle.
* 2 fois sinus car en trouvant le coté opposé a O on a la moitié d un coté de l'hexagone.
Je démontre la ou pas ?
* 6 car l'hexagone compte 6 triangles isocèle (d'angle au sommet 360°/6)
* le demi-côté est égal à sinus(360°/12)*1 (parce que rayon=1)
donc 2 fois plus pour le côté de l'hexagone
donc la réponse a la 1 er question serai:
* Sinus car c est le moyen de trouvé la longueur du coté opposé a l angle de centre O.
* 360 ° car cest la somme de tout les angles de centre O.
* 12 car l'hexagone compte 12 triangle rectangle.
* 6 car l'hexagone compte 6 triangles isocèle (d'angle au sommet 360°/6)
* 2 fois sinus car en trouvant le coté opposé a O on a la moitié d un coté de l'hexagone.( demi-côté = sinus (360°/12)*1 )
pk 6 ? il n est pourtant pas dans la formule, et on ne se sert pas de triangle isocèle ?
La réponse est complète ? Je démontre la ?
d'abord les angles et après pour le sinus
6 c'est le nombre de côté de l'hexagone (il faut partir de 6)
ne parle pas des 12 triangles rectangles
seulement un seul pour calculer le sinus et le demi-côté
donc la réponse a la 1 er question est:
* 360 ° car cest la somme de tout les angles de centre O.
* 6 car l'hexagone compte 6 triangles isocèle (d'angle au sommet 360°/6(triangle isocèle = 2 triangle rectangle)
* Sinus car c est le moyen de trouvé la longueur du coté opposé a l angle de centre O.
* 2sinus car en trouvant le coté opposé a O on a la moitié d un coté de l'hexagone.(demi-côté = sinus (360°/12)*1 )
Voila rien n'a été oublié ? et c sur que je démontre ? c est pas par un calcul d habitude ?
le plan est bon
l'hexagone étant régulier, on peut le diviser en 6 triangles égaux
d'angle au centre = 360°/6 = 60° et de 2 côtés égaux au rayon
chaque triangle isocèle se divise en 2 triangles rectangles
ayant pour hypoténuse le rayon, un angle de 60°/2=30°
et le côté opposé qui est la moitié d'un côté de l'hexagone ...
ok question 2 :
Les triangle son isocèle donc les angle de base sont égaux.
180 - 60 = 120 / 2 = 60
Les angle de chaque triangle isocèle sont de 60 ° donc est un triangle équilatéral.
Par conséquent les cotés de l'hexagone sont = 1 comme le rayon.
P = 6 * 1 = 6 cm
P/2 = 3 cm
Exacte ?
je peux pas dire le contraire
parce qu'on est parti d'un cas particulier avec l'hexagone
mais je te conseille d'utiliser la formule trouvée à la question 1
1 côté = 2*sin(360/12) = 2*sin(30°) = 2*0,5 = 1
donc p=6 et p/2 = 3
(à cause des questions suivantes)
on cherche à déterminer  à la manière d'Archimède
à la manière d'Archimède
à partir d'un polygone régulier
plus il aura de côtés, plus on aura de précision
pour l'instant avec 6 côtés on trouve 3
la différence entre  et 3 est
et 3 est 
pour n=6 

 0,142
0,142
 c'est l'écart ou l'erreur entre le vrai pi et le pi trouvé
c'est l'écart ou l'erreur entre le vrai pi et le pi trouvé
j'ai envoyé un mail a mon prof pour savoir si on devait faire un calcul a la Q°1 pour démontré apparement oui ...
mais le quel ? (la question 4 se recoupe avec la 4 et 5 donc...)
on les a fait les calculs
calcul de l'angle et calcul du sinus
pour la 4 c'est comme avec 6 côtés mais avec n au lieu de 6
donc pour la question la démonstration ce n'est pas comme une démonstration pour prouvé qu une fonction est croissante ?
non on parle pas de fonction
c'est un calcul approché de 
pour n côtés, l'angle au centre pour les triangles isocèles est de:
360/n
le demi-angle pour le triangle rectangle est de:
360/2n
demi-côté = sin(360/2n)
côté = 2*sin(360/2n)
périmètre = n*2*sin(360/2n)
demi-périmètre = n*2*sin(360/2n)
Bonjour
un peu de patience je reviens dans quelques instants
en attendant tu peux chercher un nombre n
tel que n*sin(360/2n) passe de 3,1414 à 3,1415
avec la calculatrice
à bientôt 
quelques valeurs:
pour n=10 ---> 3,0901699
pour n=20 ---> 3,1286893
pour n=30 ---> 3,1358538
pour n=50 ---> 3,1395259
c'est pas encore suffisant
pour n=100 ---> 3,1410759
pour n=200 ---> 3,1414634 <--- entre ici
pour n=300 ---> 3,1415352 <--- et là
n se situe entre 200 et 300
je te laisse chercher la valeur exacte de n
on doit avoir 3,1415... qui apparait pour la 1ère fois
c'est fait la question 4, à 20h54
pour n côtés, l'angle au centre est égal à ...
à la dernière ligne il faut enlever le *2:
demi-périmètre = n*sin(360/2n)
ok ! je revien 2 m sur la question 4 (dsl si je suis lent  )
)
* le demi-angle pour le triangle rectangle est de:
360/2n ====> correspond a l angle du triangle rectangle de centre o ?
périmètre = n*2*sin(360/2n)
demi-périmètre = n*2*sin(360/2n) /2
pour le demi on dive le périmétre par 2 ?
oui mais ...
* l'angle pour le triangle rectangle est égal à:
la moitié de l'angle au centre
(360/n):2 = 360/2n
oui mais ...
* l'angle pour le triangle rectangle est égal à:
la moitié de l'angle au centre
(360/n):2 = 360/2n
Autrement dit la moitié de l angle O du triangle Isocéle (ou Equilatéral) ?
Donc ma réponse définitive a la Q°4 :
* 360/ n ==> est egale a l angle au centre pour n coté.
* 360/2n ==> correspond a la moitié de l'angle O du triangle équilatéral choisi (donne 2 triangle Rectangle.)
* sin (360/(2n)) ==> correspond au demi coté
* 2sin (360/(2n)) ==> correspond au coté de l hexagone.
* n(2sin (360/(2n))) ==> correspond au périmètre l hexagone.
* (n(2sin (360/(2n)))) / 2 ==> correspond au demi périmètre l'hexagone.
Voila la réponse a la question 4 ?
Donc ma réponse définitive a la Q°4 :
* 360/ n ==> est egale a l angle au centre pour n coté.
* 360/2n ==> correspond a la moitié de l'angle O du triangle isocéle choisi (donne 2 triangle Rectangle.)
* sin (360/(2n)) ==> correspond au demi coté
* 2sin (360/(2n)) ==> correspond au coté de l hexagone.
* n(2sin (360/(2n))) ==> correspond au périmètre l hexagone.
* (n(2sin (360/(2n)))) / 2 ==> correspond au demi périmètre l'hexagone.
Voia comme ça c fais je l oublie pas !
passont a la question 5 !