100 rectangles sans 100 triangles

 Niveau énigmesPartager :
			        
100 rectangles sans 100 triangles
Posté par 
Imod  10-06-25 à 18:23
Bonjour à tous .

Peu d'activité ici en ce moment 

Un petit problème pour s'occuper l'esprit :

Un polygone peut être découpé en 100 rectangles mais pas en 99 . Peut-il être découpé en 100 triangles ?

On s'amuse comme toujours sans blankage inutile 

Imod
 Posté par 
GBZMre : 100 rectangles sans 100 triangles  11-06-25 à 11:07
Bonjour,

Je ne vois pas comment un peigne à 99 dents pourrait être découpé en 100 triangles.
 Posté par 
Imodre : 100 rectangles sans 100 triangles  11-06-25 à 11:32
Bien sûr GBZM mais le peigne peut être vraiment bizarre avec une forme biscornue et des dents vers l'intérieur . Tu as l'idée mais il faut développer un peu plus 

Imod 
 Posté par 
Imodre : 100 rectangles sans 100 triangles  12-06-25 à 10:09
Quelques pistes pour faire bouger les lignes 

La solution n'est pas difficile mais elle demande de bien poser les bases :

1°) Quels sont les polygones qui peuvent être découpés en un nombre fini de rectangles ?

2°) De quel côté se situe la limitation en nombre de rectangles ? 

3°) Quel élément peut faire bouger cette limite ?

Il y a encore un ou deux paramètres à faire intervenir mais chaque chose en son temps 

Imod
 Posté par 
verdurinre : 100 rectangles sans 100 triangles  14-06-25 à 16:52
Bonsoir,

pour avoir un nombre minimum de rectangles différent de 1 le polygone doit-être non-convexe.

Si le nombre minimum de rectangles est k alors il y a au moins k-1 angles rentrants.

On en déduit qu'il faut au moins k+1 triangles pour le recouvrir ( le minimum est possible. )

Tout ça est imprécis mais c'est un début.
 Posté par 
verdurinre : 100 rectangles sans 100 triangles  14-06-25 à 17:20
De fait il existe des polygones qui peuvent être découpé en 100 rectangles mais pas en 99 et qui peuvent être découpé en 100 triangles.
 Posté par 
Imodre : 100 rectangles sans 100 triangles  14-06-25 à 17:36
Je ne pense pas 

Si tu pouvais donner un exemple simple avec des entiers plus petits pour voir l'idée que tu as en tête ...

Imod 
 Posté par 
verdurinre : 100 rectangles sans 100 triangles  14-06-25 à 18:49
Un exemple :

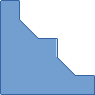
Il faut au moins quatre rectangles pour recouvrir ce polygone et il évident qu'on peut le recouvrir avec quatre triangles.
 Posté par 
Imodre : 100 rectangles sans 100 triangles  14-06-25 à 19:02
Attention , le problème n'est pas de recouvrir la figure avec quatre rectangles mais de découper la figure en quatre rectangles .

Imod 
 Posté par 
verdurinre : 100 rectangles sans 100 triangles  16-06-25 à 20:46
J'ai fait une erreur grossière . 

Les cotés des rectangles sont donc parallèles à deux directions orthogonales. 

Si le polygone peut-être découpé en k rectangles et pas en k-1 il y a au moins k-1 angles droits rentrants et k+1 angles droits saillants. 
  Posté par 
Imodre : 100 rectangles sans 100 triangles  17-06-25 à 16:47
C'est un bon départ : deux côtés consécutifs du polygone sont toujours perpendiculaires , ses angles mesurent donc 90° ou 270° . En fait pour chaque polygone , le nombre de côtés définit parfaitement le nombre d'angles de chaque sorte ( et réciproquement ) : il n'y a qu'un paramètre . Que se passe-t-il si on coupe ce polygone en deux polygones du même type ( 90° et 270° ) ?

Imod