Bonjour,
Celle-là elle est facile

 Cliquez pour afficher

Comme les v et les f ne sont pas nominatifs:
1/ff fg gg
1 bis/fg ff gg soit la même
2/fg fg fg      
donc 50%

Bonsoir.

 Cliquez pour afficher

Il y a possibilités pour le premier véhicule, puis pour le deuxième et une seule pour le troisième.
Soit 126 répartitions possibles.

Pour avoir une répartition (fg; fg ; fg) il y a choix possibles pour le premier véhicule, puis pour le deuxième et une seule pour le troisième.
Soit 36 possibilités
D'où la probabilité d'avoir un garçon et une fille dans chaque véhicule :
36/126=3/7.

L'autre probabilité demandée {ff ; fg ; gg} est la probabilité de l'événement contraire.
C'est donc 4/7.

10/10 pour quelle réponse ?
On a 2 réponses différentes, et en voici une 3ème

 Cliquez pour afficher

On a 3 filles f1 f2 f3, et 3 mecs quelconques.

Regardons spécifiquement f1
Soit elle est avec une fille (40% des cas), soit elle est avec un garçon (60% des cas).
Si elle est avec une fille, on est dans la configuration FF+FG+GG, fin des calculs.
Si elle est avec un garçon, regardons spécifiquement f2.
Soit f2 est avec une fille (33% des cas) soit elle est avec un garçon

Donc la probabilité d'avoir FF+FG+GG est 40%+60%*0.33 = 60%.
Et la probabilité d'avoir FG+FG+FG, c'est le complémentaire, c'est 40%.

je serais plutôt d'accord avec les réponses données par Verdurin dans son second post

En fait, ok avec le raisonnement de Verdurin,

 Cliquez pour afficher

mais il a fait 2 erreurs de calcul.
C(6,2)*C(4,2)=15*6=90  et pas 126
36/126=3/7 ... non.

Du coup, 36 cas 'positifs', sur 90 cas en tout, ça donne 40%,

Pourtant

Il n'y a que deux façons de monter à bord:

 Cliquez pour afficher

*soit la première voiture est composée de deux  personnes du même sexe
et les deux autres voitures  suivent la logique jaune.
*soit la première voiture est panachée et la seule solution non-jaune est la verte.

salut  Dpi , ok pour la solution en verte mais de combien de facons ?

Il n'y a que 2 façons... ça ne veut pas dire que les 2 façons ont une probabilité de 50%.

Je lance 2 pièces de monnaie, il y a 3 résultats possibles (Pile-Pile, Face-Face ou Pile-Face), et les probabilités respectives sont 25%, 25% et 50%, et pas 33% pour chaque possibilité.

Pour toutes ces questions, une des façons d'y voir clair, c'est de bien différencier les objets : je lance une pièce jaune et une pièce blanche, quels sont les résultats possibles
Jaune-Pile + Blanche Pile
Jaune-Face + Blanche Pile
Jaune-Pile + Blanche Face
Jaune-Face + Blanche Face

et là, on voit bien apparaître 25% + 25% + 50%.. parce que les 4 ppropositions sont équiprobables.

Pour l'exercice posé , c'est pareil ; on a 3 filles (F1 F2 et F3) et 3 garçons (G1 G2 G3)
Quelles sont toutes les dispositions ... les 90 dispositions comptabilisées par Verdurin. Et ces 90 dispositions sont équiprobables.

Et sur ces 90 dispositions, on constate que 36 correspondent à une des 2 configurations, et 54 à l'autre.

salut

sans distinguer on peut simplement faire l'arbre suivant :



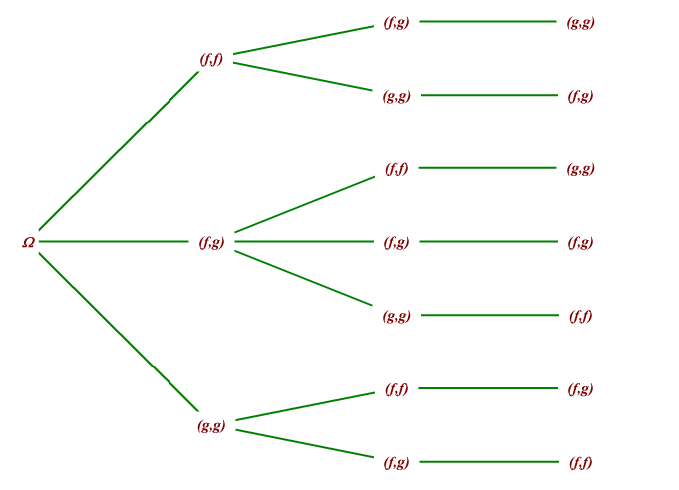
pour la première voiture on a trois choix : deux filles, ou deux garçons ou une fille et un garçon ... et ainsi de suite ...

et on peut donc raisonner dans l'univers des couples :

trois couples de filles, trois couples de garçons et 9 couples de (F, G) = (G, F) ...

Le problème de cet arbre, c'est qu'on ne conait pas la probabilité de chaque branche.

Regardons simplement la 1ère voiture : on a 3 possibilités : ff, fg ou gg.
Est-ce que les probabilités sont 33% pour chacune des 3 branches ?   Non.

Pour s'en convaincre, on va faire un autre exercice. On a 20 voitures, 30 filles et 10 garçons.
Le premier niveau de l'arbre est donc le  même : 3 possibilités pour la 1ère voiture  ff, fg ou gg.
Est-ce que la probabilité de ff dans l'exercice original ou dans ce 2ème exercice est la même ? Non.

3 branches, ça ne veut pas dire une probabilité de 33% ppour chaque branche.

7 feuilles  ici à la fin de l'arbre, ça ne veut pas dire une probabilité de 1/7 pour chaque feuille.

Ok, d'accord.

salut à tous : ( je me suis empressé de répondre favorablement à Verdurin mais je n'ai pas fais attention aux erreurs de calcul qu'il a commises
correction :
1)P( FG FG FG)  = (C3,1)².C(2,1)².C(1,1)² /C(6,2).C(4,2).C(2,2)= 9*4/90 = 2/5

2)P(FG GG FF  )= 6* (C(3,1) *C(3,1)*   (C2,2)  *  C(2,2))/90=54/90 = 3/5

Dans l'arbre de carpediem,
On peut observer qu'il n'y a que deux positions  pratiques:
Les voitures sont garées les portes ouvertes.
Deux individus entrent dans celle qui est la plus poche.
Ils déterminent  la suite du chargement.
1/FF ou GG donnent exactement la même configuration     FF GG GF
2/GF en donne 2 :   soit encore la même  FF  GG
                                           soit    GF GF
Il n'y a donc que 2 configurations au final.

Si on veut vraiment compliquer le post.....

Une ALFA  ,Une BENTLEY,une CITROEN  sont garées devant la maison .
ABEL,BERNARD, CHARLES, ANNE,BRIGITTE et CLARA  montent par deux.
Aucun lien particulier dans la bande...
Quelle est la probabilité  que BERNARD  et CLARA se retrouvent à bord de L'ALFA  

Bonjour

Je n'ai pas regardé les solutions précédentes et voilà comment je vois la chose :

On met une personne dans chaque voiture . Il y a deux possibilités : les trois personnes sont de même sexe ( une chance sur 10 ) , les personnes ne sont pas de même sexe ( 9 chance sur 10 ) . Dans le premier cas tout est bon et dans le deuxième il y a une chance sur 3 pour que tout se passe bien . Bilan 40% de chance .

Imod