Inscription / Connexion Nouveau Sujet
Aire minimale d'un polygone.
Bonjour,
j'ai quelque problème avec un exercice que l'on nous a donné ce matin pour demain. La prof nous a lâché ça avec un "Ca occupera votre journée." suivi d'un grand sourire..
Enfin bref.
Voici l'exercice :
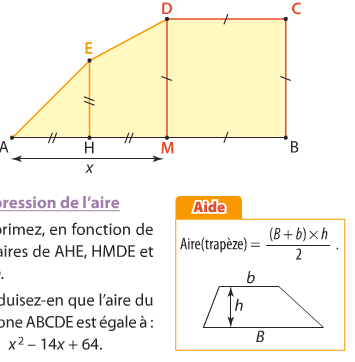
[AB] est un segment de longueur 8cm. M est un point variable de [AB]
On construit suivant le schéma, le carré MCBD, le triangle rectangle isocèle AHE et le trapèze rectangle HMDE.
On pose AM=x
On s'intéresse aux variations de l'aire de ABCDE
1. a) Exprimez, en fonction de x les aires de AHE, HMDE, et MBCD.
b) Déduisez en que l'aire du polygone ABCDE est égale à : x²-14x+64
2. On note f(x) l'aire du polygone ABCDE
a) Sur quel intervalle est définie la fonction f?
b) Dressez le tableau de variations de f. Pour quelle valeur de x l'aire de ABCDE est-elle minimale?
Quelle est la valeur de cette aire minimale?
J'ai fait le 1.a) et je me retrouve à devoir additionner ceci :
Et là, c'est le drame. J'ai un mal fou à trouver la clef qui débloquera tout ça .. sans me retrouver avec quelque chose de pire que ce que je n'ai déjà. Je connais le résultat, mais je n'ai aucune idée de comment y arriver.
Quand au 2 .. je ne vois pas non plus. J'aurais tendance à dire que la fonction f est définie sur l'intervalle 
, (puisque regroupe tous les nombres possibles et inimaginable.. ) mais ça me semble un peu trop simple..
Voilà, je compte sur votre aide, merci 
Je viens de me rendre compte qu'il n'y a même pas la suite de l'exercice ..
*** Le voici. ( Le 97 )
Désolé pour le triple-post ..
* Océane > scan de devoir non autorisé ! *
Bonsoir,
1)a)
On a : Aire triangle AHE = .
Aire trapèze HMDE = .
Enfin Aire carré MBCD = MB² = (8-x)² = x²-16x+64.
Au final,
Aire du polygone ABCDE = Aire AHE + Aire HMDE + Aire MBCD = .
D'où le résultat recherché. (Il te restait juste à développer ton 1er terme)
2)a) Non, la fonction f n'est pas définie sur R ici, comme AB=8, la distance AM=x varie donc de 0 à 8. Par conséquent, f est définie sur [0;8].
b) Comme tu n'es qu'en seconde (la méthode la plus rapide ne sera vu qu'en 1ère avec la notion de dérivée), il faut que tu écrives ici l'expression x²-14x+64 sous forme canonique, càd l'écrire sous la forme : , où les pointillés représentent des nombres réels à déterminer.
Ainsi, tu pourras facilement voir en quel valeur de x où il y a un minimum (valeur de x où l'aire de ABCDE est minimale), et en déduire quelle est la valeur de cette aire minimale.
J'ai recherché quelques petites choses sur internet..
La forme canonique :
Je trouve : (x-8)² -0
Soit (x-8)²
La dérivée :
C'est la première fois que j'essaye .. je ne suis absolument pas sûr.. :
Je trouve : 2x - 16 + 0
Soit 2x - 16
Je ne trouve pas la même chose, je doute que ce soit juste .. mais j'ai pourtant appliqué ce que j'ai pu voir ( sur internet en 5 minutes )
Annuler
connectez vous