Inscription / Connexion Nouveau Sujet
alignement des milieux des hauteurs
Bonjour, quelqu'un peut m'aider sur cet exercice d'une phrase sur les vecteurs "Existe-t-il un triangle dont les milieux des hauteurs soient alignés", merci d'avance.
Bonjour,
La question est "Existe-t-il un triangle dont les milieux des hauteurs soient alignés ?".
La réponse est donc « oui ». Et tu expliques quel type de rectangle.
Bonjour,
Oui, répondre à la question initiale est fait.
Mais falilou1 a posé une question supplémentaire que je traduis :
"Existe-t-il un triangle non rectangle dont les milieux des hauteurs soient alignés" ?
Bonjour,
La réponse à la dernière question est non. Je me suis tourné vers les complexes (sur le cercle unité) avec affixes des sommets
J'ai obtenu (après quelques calculs pénibles) :
Je ne sais pas répondre à la question au niveau première.
Bon, j'ai compris l'équivalence entre (a+b)(b+c)(c+a)=0 et le triangle est rectangle
Sinon, je ne vois pas du tout quels calculs faire.
Une indication serait la bienvenue 
J'étais en embuscade 
Couic!
Évidemment ce message n'est pas du tout destiné à falilou1.
Je n'ai pas vraiment fait dans la dentelle...
sont sur le cercle unité en sorte que les conjugués de leurs affixes soient leurs inverses.
est l'orthocentre du triangle
.
est le symétrique de l'orthocentre par rapport au côté
est le pied de la hauteur issue de
.
est le milieu de la
hauteur.
L'écriture complexe de la symétrie d'axe :
d'où (On peut aussi se référer à ce fil :
![]() Une relation d’orthogonalité avec les complexes)
Une relation d’orthogonalité avec les complexes)
est le milieu de
:
est le milieu de
(et permutation circulaire):
(ici, quelques calculs intermédiaires non retranscrits).
et compte tenu que les points sont deux à deux distincts :

salut,
j'ai pris A0;0), B(1;0), C(x;y)
je trouve comme condition (hors triangle aplati) x^2+y^2-x=0 cad ABC triangle rectangle en C
J'ai compris la solution de lake 
Pour celle de alb12, j'avoue patauger un peu.
Ne serait-il pas plus simple de choisir A(-1;0), B(1;0), C(c;d) pour trouver c2+d2 = 1 ?
Présenter cette solution pour qu'elle soit abordable par falilou1 vous semble-t-il possible ?
je n'ai pas essaye de faire les calculs à la main
le script peut etre ecrit par un eleve de seconde
le resultat (le determinant) peut etre interprete par un eleve de premiere
en revanche les calculs (en particulier celui du determinant) relevent plus de la premiere annee du superieur
avec -1 pour affixe de A on obtient ![]()
Juste un petit commentaire sur "mes calculs" :
Je savais dès le départ que, dans le cadre du "truc de Morley circonscrit", rectangle revenait à prouver que
en étant bien convaincu que les seuls triangles solutions étaient rectangles. On obtient très naturellement un polynôme homogène de degré 4 en
où la factorisation (ici) par
est quasiment "évidente"
Le reste coule de source
Sans logiciel de calcul formel, on arrive là aux limites de ce qu'il est possible de faire manuellement 
Bonsoir,
J'ai pris un peu plus de temps pour regarder les calculs analytiques du second lien, celui avec A(-1;0) et B(1;0).
Le calcul du déterminant n'est pas si monstrueux qu'il semble au premier abord.
Avec V1( X1 ; K1
 y(x2+y2-1) )
y(x2+y2-1) )
et V2( X2 ; K2
 y(x2+y2-1) ),
y(x2+y2-1) ),
La factorisation par y(x2+y2-1) apparaît facilement. Puis la factorisation complète.
Les calculs qui précèdent ne sont pas vraiment agréables.
Je les ai faits "à la main", mais j'ai préféré travailler avec les vecteurs H1H3 et H3H2 à la fin.
Pour répondre à mathafou :
On part d'un triangle non aplati, non rectangle en A, ni en B.
A(-1;0), B(1;0) et C(x; y) avec y, x+1 et x-1 non nuls.
On démontre que si les milieux des hauteurs sont alignés alors le point C est sur le cercle de diamètre AB.
Ça démontre bien ce qu'on voulait.
Bonjour à tous,
Il me semble qu'on peut traiter les choses de façon géométrique aussi
évidemment ABC est un triangle non aplati...
on sait que les symétriques de l'orthocentre H par rapport aux côtés sont sur le cercle circonscrit du triangle.
donc si les milieux des hauteurs sont alignés, les symétriques de l'orthocentre par rapport aux côtés qui s'en déduisent par une homothétie de centre H et de rapport 4 sont aussi alignés
étant alignés et sur le cercle, cela signifie qu'il y en 2 de confondus et par conséquent deux pieds de hauteurs qui sont confondus... d'où le résultat
sauf erreur 
ah non mince... oubliez... j'ai considéré les milieux des segments [orthocentre ; pied de hauteur]

énoncé mal lu 
10 coups de bâton !
Merci pour le lien 
Pitié pour les élèves de 1ère !
Je suis persuadée qu'une démonstration géométrique, sans calcul, est possible.
De la à la trouver...
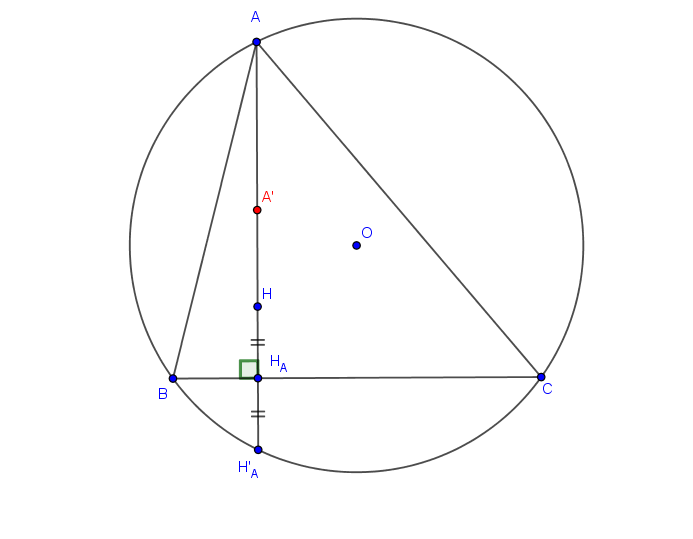
Une figure peut peut-être déclencher des idées :
Bonsoir à toutes et à tous,
Juste pour tenter d'égayer votre soirée en cette triste époque.
10 coups de bâton !
Pas assez cher mon fils. Je propose 20.
Mais dans mon immense mansuétude, je te laisse le choix :
20 coups de bâtons ou 100 coups de fouet ?

Bonsoir à toutes et à tous,
Juste pour le fun (je n'apporte évidemment rien de nouveau) :
J'ai erré à droite à gauche sur ce sujet et entre autres je me suis intéressé au centre du cercle avec les notations de la dernière figure de Sylvieg.
Figure-t-il dans ETC le plus ou moins célèbre site de Clark Kimberling : Encycopedia of Triangle Centers ici: ![]() ?
?
Je l'ai trouvé; il s'agit de X(5893) :
X(5893) = CENTER OF HALF-ALTITUDE CIRCLE
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = -2a10 + 3b10 + 3c10 - a8b2 - a8c2 + 12a6b4 + 12a6c4 + 16a6b2c2 - 10a4b6 - 10a4c6 + 10a4b4c2 + 10a4b2c4 - 2a2b8 - 2a2c8 + 16a2b6c2 + 16a2b2c6 + 28a2b4c4 - 9b8c2 - 9b2c8 + 6b6c4 + 6b4c6
The half-altitude circle is the circumcircle of the half-altitude triangle. Its radius is
[R/(16SASBSC)][2(b2c2J2 + S2 - S2A)(c2a2J2 + S2 - S2B)(a2b2J2 + S2 - S2C)]1/2, where J = |OH|/R (as at X(1113).
X(5893) lies on these lines: {2,5894}, {4,6}, {5,3357}, {30,5448}, {64,3091}, {140,2777}, {154,3146}, {221,5225}, {546,5462}, {1853,3832}, {2192,5229}
X(5893) = midpoint of X(4) and X(2883)
X(5893) = complement of X(5894)
X(5893) = X(11260)-of-orthic-triangle if ABC is acute
Vous pouvez remarquer qu'il y figure une expression assez compliquée du rayon.
Au dénominateur, on ne trouve que le produit
Encore une fois, c'était juste pour le "fun"

Bonjour,
Ci-dessous, une piste avec Ménélaüs et les milieux des côtés, que je n'arrive pas à finaliser :
Donc A', B', C' alignés est équivalent à A1, B1, C1 alignés.
Et après ?



