Inscription / Connexion Nouveau Sujet
Angle orienté .
Bonjour ,
Merci.
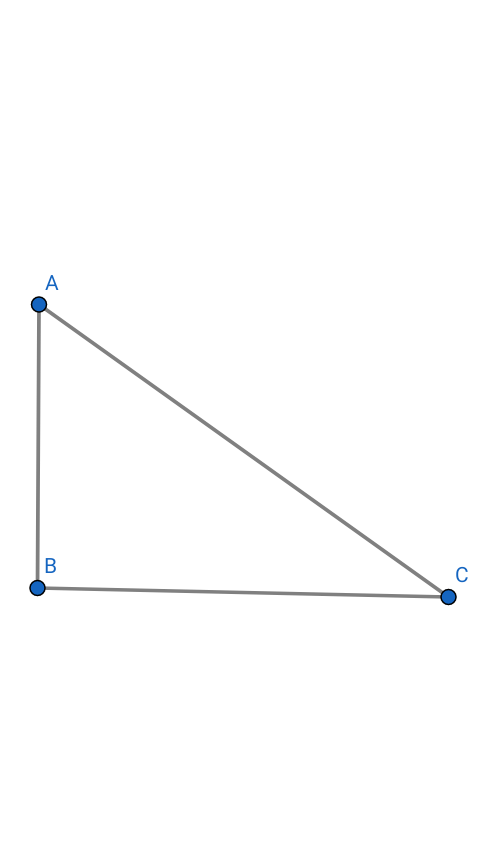
ABC est un triangle rectangle en B sur la figure ci-dessous , déterminer les mesures en degré et en radian de 10 angles de ce triangle.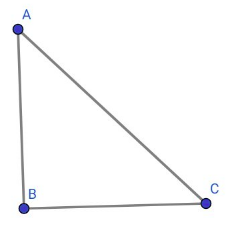
*image recadrée*
Bonjour,
on aimerait un énoncé exact et recopié mot à mot en entier avec la figure de l'énoncé et pas une reconstitution approximative !!
et ce dès le départ.
la figure proposée ressemble plus à un triangle rectangle isocèle (45°-90°-45°) qu'à un triangle avec un angle de 60° ! angle que l'on découvre au hasard de la discussion au lieu d'être défini au départ. !!
ni quels seraient bien les 9 ou 10 ou va savoir combien angles à calculer !
faut arrêter de se f... du monde !
La méthode des aiguilles d'une montre (direct : dans le sens contraire des aiguilles d'une montre et
Indirect : dans le sens des aiguilles d'une montre.)
Mais l'énoncé ne demande pas de calculer les angles , plutôt de déterminer la mesure des 9 angles dans ce triangle .
Je propose mes°(AB,AC)=60° et mes (AB,AC)=-π/3 puisque c'est dans le sens des aiguilles d'une montre.
En regardant la figure. Mais on peut choisir le sens de rotation.
Si on va de AB à AC dans le sens direct, on obtient la mesure principale de l'angle (AB,AC).
Mais on peut aussi tourner dans le sens indirect; on obtient alors la valeur principale de l'angle plus 2 correspondant à un tour.
correspondant à un tour.
D'une manière générale, on peut effectuer k tours et ajouter 2k à la mesure principale.
à la mesure principale.
Merci .
Je comprends mieux maintenant
J'ai pu déterminer toutes les mesures sauf celle de l'angle (BA,AC).
Pourriez vous m'aider ?
Même méthode (règle de Chasles appliquée aux angles orientés) :
(BA,AC) = (BA,AB) + (AB,AC) = . . . .
A 13h01, tu m'as dit que l'angle BCA valait 60°, c'est-à-dire  /3 .
/3 .
C'est donc  /6 que vaut l'angle BAC, et non
/6 que vaut l'angle BAC, et non  /3 !
/3 !
Si je comprends bien pour trouver (BA,AC)=(BA,AB)+(AB,AC)=π-π/6=5π/6 . Merci , n'y a t il pas une autre méthode plus simple que çà ?
Une méthode plus simple ? Mais celle que je te propose n'est vraiment pas compliquée !
7 /6 ou - 5
/6 ou - 5 /6 : c'est juste.
/6 : c'est juste.
Choisis plutôt - 5 /6, car cette valeur, comprise dans l'intervalle ]-
/6, car cette valeur, comprise dans l'intervalle ]-  ;
;  ], est la valeur principale de l'angle orienté.
], est la valeur principale de l'angle orienté.