Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Angles orientésTopics traitant de angles orientés [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Angles orientés

Posté par
la-miss-du-23 22-02-08 à 14:16

Bonjour, un petit souci avec un exercice pourriez- vous m'aider?

ABC est un triangle direct rectangle en A, tel que AB=2AC.
ADC est un triangle direct isocèle et rectangle en C et BAE est un triangle équilatéral direct. Donner en justifiant la mesure principale des angles suivants:
(AD;AE) , (CB;AD) , (EA;BC) ~~> se sont des vecteurs


Pour (AD;AE) je trouve -13/12
Par contre je ne sais pas comment faire pour les deux autres?

Je joins un dessin.

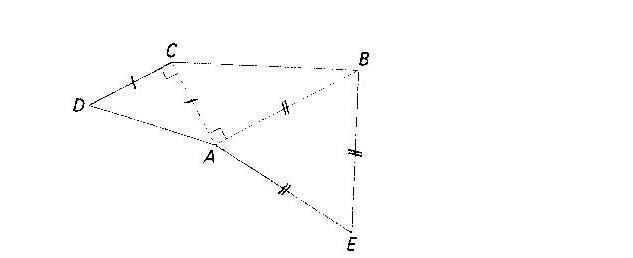
Angles orientés

Posté par
la-miss-du-23Angles orientés 22-02-08 à 19:54

Bonsoir, j'ai un souci avec un exercice de mon DM de maths! Pourriez-vous me donner un petit coup de main?

EXERCICE
ABC est un triangle direct rectangle en A, tel que AB=2AC.
ACD est un triangle direct isocèle et rectangle en C et BAE est un triangle équilatéral direct.
Donner en justifiant la mesure principale des angles suivants:
(AD;AE) , (CB;AD) , (EA;BC) (ce sont des vecteurs)

Pour (AD;AE) je trouve -13/12
Pour les deux autres je ne sais pas comment faire?

*** message déplacé ***

Posté par
la-miss-du-23Angles orientés 22-02-08 à 19:58

je n'arrive pas a insérer le dessin

*** message déplacé ***

Posté par
padawanre : Angles orientés 22-02-08 à 20:04

Bonsoir,
regarde si ton image est bien au format .jpg.
Sinon, ouvre ton image sous paint et enregistre-là en changeant son format en .jpg et poste-là ici.

*** message déplacé ***

Posté par
Marcel Moderateurre : Angles orientés 22-02-08 à 21:53

Curieux : Angles orientés

*** message déplacé ***

Posté par
Marcel Moderateurre : Angles orientés 22-02-08 à 21:55

Multi-post : (Lien cassé)

Posté par
la-miss-du-23Angles orientés 22-02-08 à 21:56

désolée je ne le retrouvait plus je pensais qu'il y avait eut un souci lorsque je l'ai posté!!!

Posté par
la-miss-du-23Angles orientés 22-02-08 à 21:56

Comment supprimer l'autre topic???

Posté par
slorevivre : Angles orientés 22-02-08 à 22:45

bonsoir
tu ne crois pas que c'est plutot dans ABC
hypotenuse=2*petit cote de l'angle droit?
sinon tes angles ils ne seront pas "ronds"ils seront approches ou alors il fut poser \alpha tel que \tan(\alpha)=0.5

Posté par
la-miss-du-23Angles orientés 23-02-08 à 10:33

Déja merci d'être intervenu. Et ensuite j'ai fait une faute de frappe
C'est ACD et non ADC.
Cependant je ne sais toujours pas comment faire?

Posté par
camillemAngles orientés 23-02-08 à 13:48

Bonjour,

L'angle (\vec{AD};\vec{AE}) =(\vec{AD};\vec{AC})+ (\vec{AC};\vec{AB})+(\vec{AB};\vec{AE})=\frac{\pi}{4}+\frac{\pi}{2}+\frac{\pi}{3}=\frac{13\pi}{12}


(\vec{CB};\vec{AD})=(\vec{CB};\vec{BA})+ (\vec{BA};\vec{AC})+(\vec{AC};\vec{AD}) avec (\vec{AC};\vec{AD})=\frac{\pi}{4} car le triangle ACD est isocèle dont angle au sommet (\vec{AC};\vec{CD})=\frac{\pi}{2}

Calul de l'angle (\vec{CB};\vec{BA}):

Poser (\vec{CB};\vec{BA})=\alphatg(\alpha)=\frac{AC}{AB} et comme AB=2AC tg(\alpha)=\frac{AC}{2AC}=\frac{1}{2} d'où \alpha= tg^-^1(\frac{1}{2})=26^o.56 (obtenu au calculatrice)

(\vec{CB};\vec{BA})= \frac{26^o.56\times \pi}{180^o}=0.463\pi

(\vec{CB};\vec{AD})= 0.463\pi+\frac{\pi}{2}+\frac{\pi}{4}=1.213\pi

(\vec{AE};\vec{BC})= (\vec{AE};\vec{EB}+(\vec{EB};\vec{BC})= -\frac{\pi}{3}-(\frac{\pi}{3}+0.463\pi)=-1.3\pi

N'hésites pas si tu as des questions
A+
Camille

Posté par
camillemAngles orientés 23-02-08 à 13:58

Re,

une erreur tout au début :

(\vec{AD};\vec{AE})= (\vec{AD};\vec{AC})+(\vec{AC};\vec{AB})(\vec{AB};\vec{AE})=-(\frac{\pi}{4}+\frac{\pi}{2}+\frac{\pi}{3})=-\frac{13\pi}{12}

A+
Camille

Posté par
la-miss-du-23angles orientés 23-02-08 à 14:38

Merci beaucoup!!

Alors j'ai quelques questions. Pour donner des mesures principales ne faut il pas que je laisse tout avec et sous forme de fraction?
Ensuite pour le dernier ce n'est pas (AE;BC) mais (EA;BC) donc cela doit changer quelque chose au résultat?

Posté par
slorevivre : Angles orientés 23-02-08 à 16:23

Bonjour ,
je relis camillemet dans la conversion degre radian \alpha =0.463rd (pas de \pi)et je ne suis pas vraiment d'accord avec les orientations
(\vec {BC};\vec {BA})=\alpha\simeq 0.463ensuite  
(\vec {CB};\vec {AD})=\pi+(\vec {BC};\vec {AD})=\pi+\alpha+(\vec {BA};\vec {AD})=\pi+(\vec {BA};\vec {AD})\pi+(\vec {AB};\vec {AD})={3\pi\over 4}+\alpha+2\pi\simeq 0.463+{3\pi\over 4}\simeq 2.81rad

Posté par
slorevivre : Angles orientés 23-02-08 à 16:33

(logique grand angle mais plus petit que 180degra)
(\vec {EA};\vec {BC})=(\vec {EA};\vec {AD})-(\vec {CB};\vec {AD})+\pi=\pi+{13\pi\over 12}-2.81+\pi\simeq 0.583rad

Posté par
slorevivre : Angles orientés 23-02-08 à 16:34

mesurre principale = resultat entre -3.14 et 3.14 en langage "simpliste "oupluto^t dans  ]-\pi;+\pi]

Posté par
camillemAngles orientés 23-02-08 à 16:55

Re,
Je suis d'accord avec sloreviv

A+
Camille

Posté par
la-miss-du-23Angles orientés 23-02-08 à 18:14

Merci beaucoup pour votre aide

Posté par
slorevivre : Angles orientés 23-02-08 à 18:59

merci camillem
pour  la-miss-du-23:
ces calculs d'angle ne sont pas faciles et pour verifier: tracer deux demidroites de meme origine  paralleles  aux supports des vecteurs , mesure au rapporteur en tournant dans le sens trigo et convertis en radian

Posté par
la-miss-du-23Angles orientés 23-02-08 à 19:07

Merci encore a camillem et sloreviv.
J'aivais eu l'idée de prolonger les segments des triangle mais pas très "inspirée" pour les exploiter.
Encore merci a vous deux!


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1718 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !