Inscription / Connexion Nouveau Sujet
Application
Bonjour !
Je veux montrer que l'application g de P(A)×P(A barre) vers P(E) qui associe à chaque (X;Y)
P(A)×P(A barre) X
Y. Sachant que AP(E).
Bon, j'ai essayé de resoudre
g(X;Y)=B pour BP(E)
Mais je n'ai rien trouvé de précis pour que l'équation admet une seule solution ?
Aidez moi svp 
Ps: la seule chose que j'ai trouvé c'est que X=B ou Y=B, mais en quoi ça m'aidera ?
Je résume ta 1ère phrase.
Je veux montrer que l'application g définie de telle façon.
Tu dis effectivement comment g est définie. Mais tu veux montrer que cette fonction g a quelle propriété ?
Bonjour
(j'imagine que tu notes )
Il faut donc montrer que pour tout dans
, il existe
dans
tels que
c'est à dire montrer qu'il existe et
tels que
Remarque que
Zormuche
Bonjour !
J'ai premièrement démontré que X
E et YE
(Car BA et XXY ainsi pour Y)
Et on a A=E
Donc X(A) et Y(A)
Est ce suffisant ?
Khola22 bonjour
on ne comprend rien à ce que tu cherches 
Tu prends une partie B de E... quelconque
trouve une partie X de A et Y de A* (je mets * à la place de barre pour aller plus vite) telles que
XY=B
fais des dessins ça ira mieux
Y=
fais un dessin bon sang !
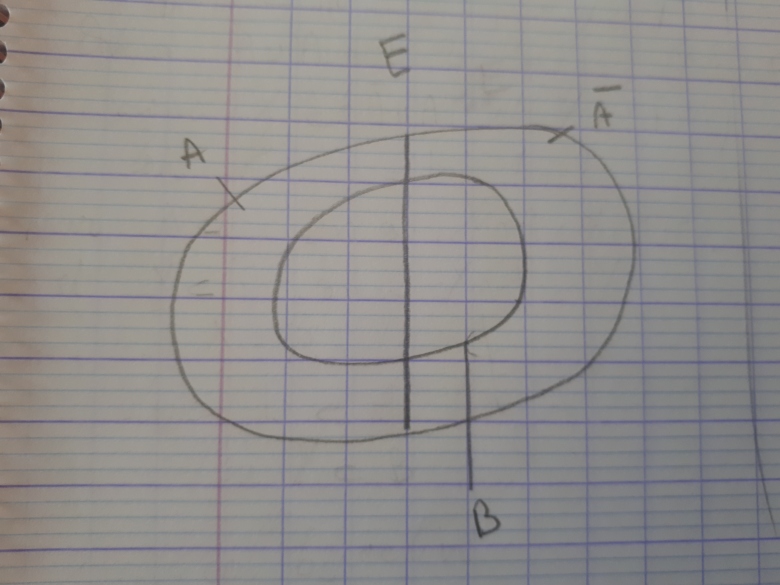
dessine une patate, c'est E
partage la en 2... un morceau c'est A, l'autre c'est A*
dessine une autre patate contenue dans E, c'est B
et poste ton dessin
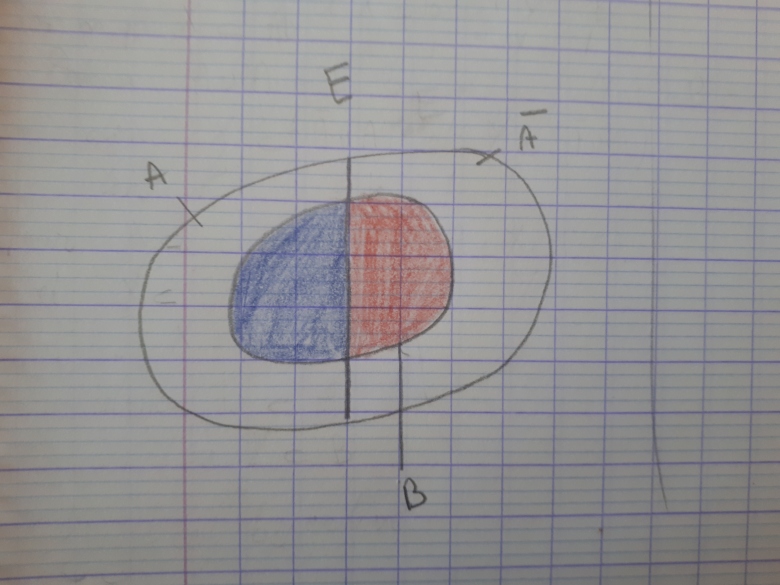
et tu ne vois pas un X contenu dans A et un Y contenu dans A* qui font que XY=B ?
colorie X en bleu et Y en rouge et poste
Oui oui je vois, c'est clair comme ça, mais une démonstration mathématique c'est comment ? C'est ça mon problème, des patates ne marcheront pas avec le professeur
Annuler
connectez vous