salut


dans l'espace affine déjà chercher les points fixes ...

carpediem en cherchant les points fixes je peux tomber soit sur un déplacement ou anti-déplacement sur un des cas d'une isométrie mais ma matrice de départ n'est pas orthogonale donc il y a pas d'isométrie

et alors ?

connaitre les points fixes est quasiment toujours un premier pas vers la connaissance d'une application affine ...

Bonjour,
Pour clarifier les écritures, noter f l'application affine dont il est question.
Et M' = f(M) .
Calculer les coordonnées de permet de trouver l'ensemble des points fixes, mais aussi de constater que ce vecteur a quelque chose d'invariant.

Bonjour,


on pourra remarquer que est la matrice d'un projecteur _{sauf erreur bien entendu}

Avec plus de recul et en suivant l'idée de carpediem _{que je salue}


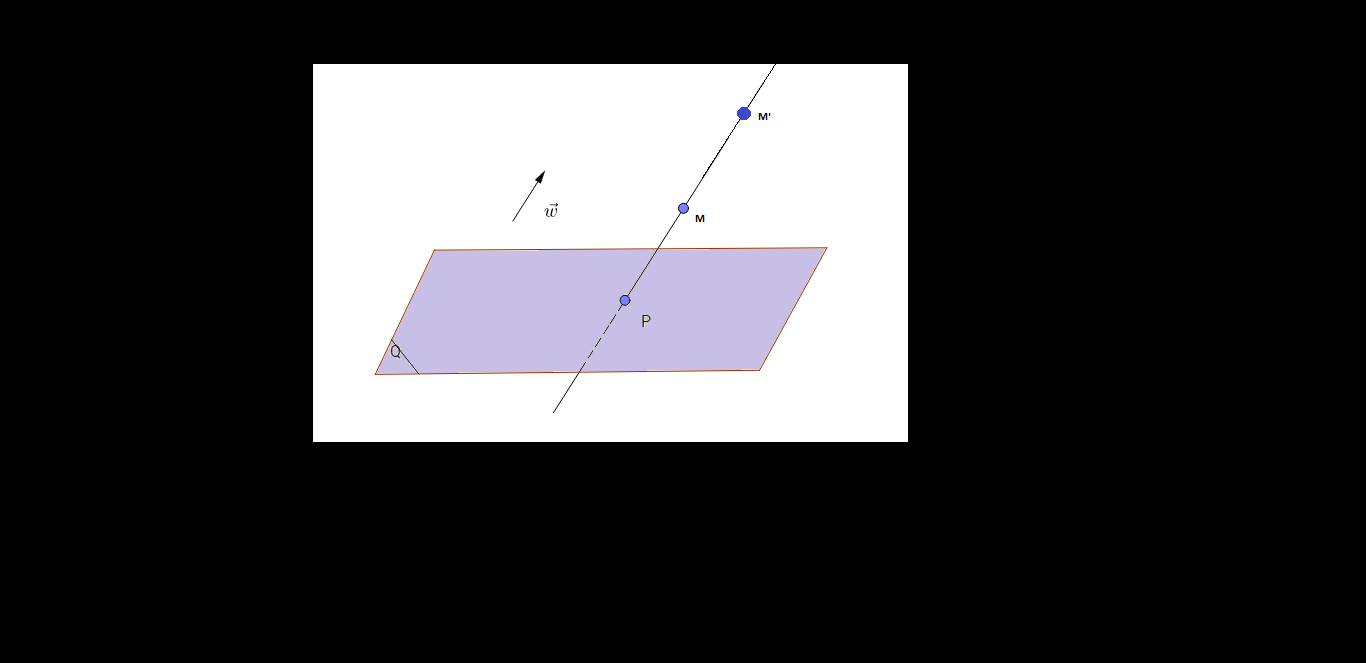
il est facile de voir que l'ensemble des points fixes de notre application affine
est le plan .



on remarque ensuite (comme le signale Sylvieg) que le vecteur admet une direction indépendante de

on vérifie en effet que où est le vecteur de coordonnées non parallèle au plan .



la droite issue de dans la direction de coupe en l'unique point

et on vérifie que .


si mes calculs sont corrects , notre application affine est appelée l'affinité de plan , de direction et de rapport _{sauf erreur bien entendu}

Oui, mais boy974 n'a pas fait grand chose

on pouvait voir que :

2x' - 2x = x + y + z - 1
y' - y = x + y + z - 1
2z' - 2z = x + y + z - 1

donc que l'espace des points fixes est le plan d'équation x + y + z - 1 = 0

et on en déduit aussi que :

2x' - 2x = x + y + z - 1
2y' - 2y = 2(x + y + z - 1)
2z' - 2z = x + y + z - 1

ou encore ce qui rejoint les résultats de elhor_abdelali et l'idée de Sylvieg

salut,

Sylvieg @ 26-05-2019 à 21:29

Oui, mais boy974 n'a pas fait grand chose