Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Reprise d'études [tout]Lister tous les topics de mathématiques
Niveau Reprise d'études
Partager :

application R^2 vers R^3

Posté par Profil machintruc 26-12-18 à 19:36

Bonjour

Vous auriez plus simple comme application à me proposer?
car dans mon exemple j'ai des puissances 4 sur mes termes
en fait j'en ai besoin pour construire des repères barycentriques fonctions d'un quelconque vecteur  

Merci d'avance sinon à défaut je prendrai mon exemple

f:\mathbb {R}^2\rightarrow \mathbb {R}^3 est une application telle que

\forall \left(  x,y\right)\in \mathbb {R}^2 et en posant f\left(x,y\right)=\left(a,b,c\right) alors

a=BC=\sqrt {x^4+2x^2+1}
b=AC=\sqrt {2x^4+y^4+4x^2+2y^2+2x^2y^2+2}
c=AB=\sqrt {x^4+y^4+2x^2+1}

sont les trois côtés d'un triangle non plat ABC

tel qu'en plus le déterminant de la matrice   \left( \overrightarrow {AB},\overrightarrow {AC}\right) est toujours strictement positif

ici je donne dans mon exemple

\overrightarrow {AB}=\begin {pmatrix}  1+x^2\\y^2  \end {pmatrix} et  \overrightarrow {AC}=\begin {pmatrix}   1+x^2\\ 1+x^2+y^2  \end {pmatrix}

donc là on a :

  \forall \left(  x,y\right)\in \mathbb {R}^2 ,  det \begin {pmatrix}  1+x^2&1+x^2\\y^2 &1+x^2+y^2 \end {pmatrix}>0

Posté par
lafol Moderateurre : application R^2 vers R^3 26-12-18 à 19:38

Bonjour
les identités remarquables, ce serait bien de les remarquer !

Posté par Profil machintrucre : application R^2 vers R^3 26-12-18 à 19:52

ah oui

(x^2+1)^2=x^4+1+2x^2

j'avais la tête dans le guidon

merci mlle,mme Lafol

Posté par
lafol Moderateurre : application R^2 vers R^3 26-12-18 à 19:55

sinon, tu ne dis pas très clairement ce que tu cherches à faire ... A,B et C sont imposés ? c'est toi qui les choisis ? si oui, quelles sont les contraintes ? juste le coup du déterminant positif ?

Posté par Profil machintrucre : application R^2 vers R^3 26-12-18 à 20:02

non rien est imposé

en partant d'un quelconque vecteur (éventuellement nul de R^2) la fonction doit permettre de construire un triangle non plat ABC de côtés a,b,c  

et oui le déterminant de \left( \overrightarrow {AB}, \overrightarrow {AC}\right) strictement positif (selon la convention d'écriture des triangles a=BC,b=AC,c=AB)sinon à part ça ...

Posté par
lafol Moderateurre : application R^2 vers R^3 26-12-18 à 20:06

pourquoi tu es parti sur des choses aussi compliquées ?
une fonction constante n'aurait-elle pas pu faire l'affaire ?

Posté par Profil machintrucre : application R^2 vers R^3 26-12-18 à 20:37

en fait ce que je veux faire c'est avoir toujours la garantie d'avoir un repère barycentrique ABC sur le plan image d'une projection conique à partir d'un vecteur \overrightarrow {P^{\prime}Q^{\prime}} éventuellement nul

P' et Q' sont les images sur le plan image par une projection conique de deux points P et Q en mouvements et qui appartiennent à  une droite de l'espace qui rencontrera le plan image

du coup c'est le mouvement de ces deux points qui définiront mon repère barycentrique sur le plan image  en posant A le point de fuite et
\overrightarrow {AB} et \overrightarrow {AP^{\prime }} de même sens et direction  

bon avec les identités remarquable ça simplifie je trouve non?

Posté par Profil machintrucre : application R^2 vers R^3 31-12-18 à 20:18

Bonjour

à propos de cette application f

en posant les trois fonctions réelles  p(x)=\sqrt {\left(x^2+1\right)^2+1}

q(x)=\sqrt {x^4+1}

g(x)=\dfrac {1}{2}\sqrt {\dfrac {\left( p(x)+q(x)-1  \right) . \left( q(x)-p(x)+1   \right) .  \left( p(x)-q(x)+1   \right)}{p(x)+q(x)+1}}

alors g(x) donne le rayon du cercle inscrit du triangle ABC

de côtés a,b,c selon  f\begin {pmatrix}0\\ x\end {pmatrix}=\begin {pmatrix}a\\ b\\ c\end {pmatrix}

cette fonction est paire et strictement positive

elle a la forme d'une cloche de limite nulle en l'infini  et vérifie g(0)=\dfrac {1}{2+\sqrt {2}}

par contre en posant g(x)=\dfrac {1}{2+\sqrt {2}}\left(x^2+1\right)

alors  g(x) donne le rayon du cercle inscrit du triangle ABC

de côtés a,b,c selon  f\begin {pmatrix}x\\ 0\end {pmatrix}=\begin {pmatrix}a\\ b\\ c\end {pmatrix}

Posté par Profil machintrucre : application R^2 vers R^3 31-12-18 à 21:13

...et en posant

a:\mathbb {R}\rightarrow \mathbb {R}

a(x)=x^2+1

b:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}

b(x,y)=\sqrt {\left(x^2+1\right)^2+\left(x^2+y^2+1\right)^2}

c:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}

c(x,y)=\sqrt {\left(x^2+1\right)^2+y^4}

r:\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}

r(x,y)=\dfrac {1}{2}\sqrt {\dfrac {\left(b(x,y)+c(x,y)-a(x)\right).\left(a(x)+c(x,y)-b(x,y)\right).\left(a(x)+b(x,y)-c(x,y)\right)}{a(x)+b(x,y)+c(x,y)}}

alors r(x,y) donne le rayon du cercle inscrit du triangle ABC de cotés a(x),b(x,y),c(x,y)

par cette application f\begin {pmatrix}x\\y \end {pmatrix}=\begin {pmatrix}a(x)\\b(x,y)\\c(x,y)\end {pmatrix}

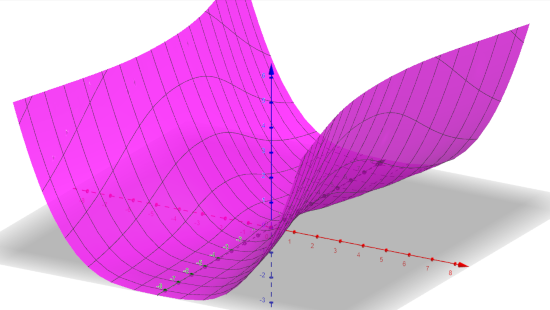
représentation de la surface engendrée dans \mathbb {R}^3 par cette application r

application R^2 vers R^3

Posté par Profil machintrucre : application R^2 vers R^3 05-01-19 à 19:29

Salut

le calcul de l'aire du triangle s'exprime très simplement

Aire du triangle ABC =\dfrac {1}{2}\left(x^2+1\right)^2

avec  f(x,y)=(a,b,c)

avec les trois côtés a,b,c du triangle non plat ABC

Posté par Profil machintrucre : application R^2 vers R^3 05-01-19 à 20:54

..et le rayon du cercle inscrit du triangle s'écrit aussi très simplement

le rayon du cercle inscrit = \dfrac {a^2}{a+b+c}

Posté par Profil machintrucre : application R^2 vers R^3 11-01-19 à 23:33

Salut

une dernière chose avant de conclure ce sujet

en se donnant

le rayon inscrit r>0 d'un triangle non plat

un réel positif u\geq 0

deux entiers i\in \{-1,1\} et  j\in \{-1,1\}

et en posant

d=r.\left(2+\sqrt {2}\right)-1

\sigma =\left\lfloor\dfrac{2\left\lfloor\dfrac{d+\left|d \right|+1}{\left|d \right|+1}\right\rfloor}{\left\lfloor\dfrac{d+\left|d \right|+1}{\left|d \right|+1}\right\rfloor +1}\right\rfloor

t=i.\sqrt {\sigma .d+u}

a=t^2+1

\delta=a^2\left(\dfrac {1}{r}\right)^2-2a. \left(\dfrac {1}{r}\right)+\dfrac {2r}{a}+\dfrac {a}{2r-a}-2

k=j.\sqrt {\dfrac {a}{2}\left(\sqrt {\delta}-1\right)}

on peut alors remarquer que

r est aussi le rayon d'un cercle inscrit d'un triangle non plat ABC tel que

a=BC

b=AC=\sqrt {a^2+\left(a+k^2\right)^2}

c=AB=\sqrt {a^2+k^4}

et on vérifiera toujours

k^4+a.k^2-\dfrac {a^2}{4}.\left(\delta -1\right)=0

Posté par Profil machintrucre : application R^2 vers R^3 11-01-19 à 23:39

edit:

le rayon r>0 d'un cercle inscrit d'un triangle non plat


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !