Merci pour l'énigme.

 Cliquez pour afficher

Le lieu de G est la bissectrice de .
C'est plus dur de le prouver

Bonsoir,

--> LittleFox : en écrivant "les positions relatives de A,F,D correspondent à celles de de A,E,B",
je voulais simplement dire que si E est entre A et B, alors F est entre A et D
et si B est entre A et E, alors D est entre A et F...

 Cliquez pour afficher

Oui pour la bissectrice de . J'ai trouvé facile à prouver, en particulier en utilisant G comme barycentre. Mais je n'ai pas trouvé de preuve purement géométrique…

vham
m'énerve ton problème
ça fait deux jours que je cherche une solution géométrique...
mais intéressant !

J'ai cette proposition avec deux losanges , je n'ai pas le temps de finaliser  :



Imod

Bonsoir. Imod, tes lettres ne sont pas celles de l'énoncé il me semble donc c'est difficile à suivre.

>wham

Les lettres de la figure semblent importantes, tu serais aimable de nous proposer ta figure

Bonjour à tous. Je voudrais m'intéresser à ce problème mais, contrairement à vous tous, je ne comprends pas l'énoncé. Je comprends que F est obtenu en partant de E, rotation + translation. Mais F n'arrive pas sur AD. Je m'excuse mais vham ou quelqu'un d'autre pourrait-il avoir l'amabilité d'être plus explicite avec un croquis si possible.
Et qu'est-ce qu'un parallélogramme direct et aussi un angle direct ?

Bonjour,

C'est une éventuelle démonstration purement géométrique que je cherche
Une démonstration par barycentre ci-blankée :

 Cliquez pour afficher

Avec les notations de la figure, E :bar((A,m),(B,a-m)) et F :bar((A,m),(D,b-m))
G est donc barycentre du triangle ABD. avec la masse a en E et la masse b en F.
Dans le repère on peut écrire directement :


En prolongeant (AD) par le segment [AO]=(a-b) on obtient OD=a et OPCD est un losange.
On peut écrire

on vérifie alors qui montre que G est sur la diagonale (OC) du losange OPCD

Bonsoir,

La réciproque est asse aisée ...
On forme un losange tel que DO=PC=DC=AB
On  trace  ses diagonales DP et OC   ,Go est leur point d'intersection.
On a un autre point G1 si  EB = DA  (autrement dit F est en A ).
On a un autre point G2 si  m=0
Ces 3 points G particuliers sont sur la diagonale OC.

Bonjour,

Pour trois points particuliers de (OC) vous prouvez BE=DF,
Mais pour un point quelconque G de la droite (OC) ?
L'intersection de (DG) et (AB) fixe E
L'intersection de (BG) et (AD) fixe F
Comment prouvez-vous alors que BE=DF ?

Bonsoir. Je ne comprends toujours pas bien ton énoncé mais cela n'est pas grave car au vu de ton dessin on voit bien le problème. J'ai une preuve analytique qui ressemble forcément à la tienne. Pour une preuve purement géométrique je n'ai pas trouvé non plus. Une idée, peut-être, serait de transformer le parallélogramme en rectangle en le "redressant" sachant que beaucoup de proportions et propriétés restent valables. Mais, même après cette simplification, rien d'immédiat ne m'apparait ...

Bonsoir,

Jai été trop perfectionniste en posant cette recherche d'une solution purement géométrique.

Pour caractériser la position de G il faut utiliser les rapports GF/GB et GE/GD, ce que la méthode du barycentre donne quasi-immédiatement. Il n'y a certainement pas "plus géométrique".

Je ne sais pas si ça peux aider mais je trouve marrant que si on inverse la position relative de F par rapport à D on obtient un lieu pour G' perpendiculaire au lieu de G. Et à leur intersection se trouve C.

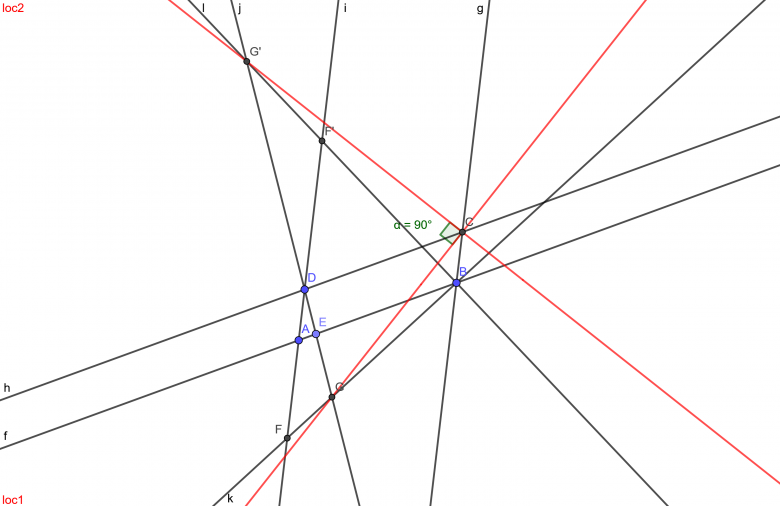
>Littlefox
comme il s'agit de la perpendiculaire à la grande diagonale du fameux losange ,tu  pourras
peut-être trouver  un truc...

Bonjour,

Un truc du genre : les diagonales d'un losange se coupent ...

Bonsoir,

dans le même repère on obtient y+x=a+b comme lieu de G'

Bonjour à tous et en particulier à vham s'il repasse par ici,

Il m'arrive de fouiner dans le forum détente. Je me permets de remonter ce fil qui fait appel à quelques notions de géométrie projective.

  D'abord une figure :

  

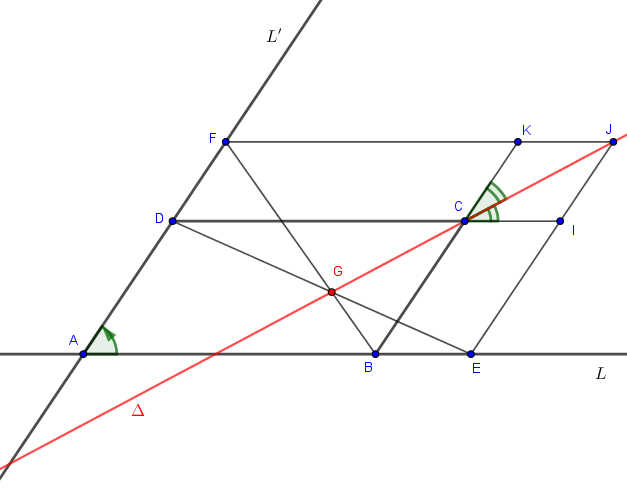
Soit la bijection affine qui envoie la droite sur la droite telle que et .
On construit son graphe : c'est la droite
Cette correspondance affine est aussi une homographie et en particulier, le graphe de est aussi son axe d'homographie : .

Donc appartient à .
Dans le cas qui nous occupe, et le quadrilatère est un losange en sorte que est la bissectrice de .

Je m'aperçois que mon  message  manque de clarté. Je reprends avec une configuration un peu plus générale.

Une application affine du plan dans lui même est définie par 3 points et leurs images .
On suppose les droites et sécantes en .

La restriction de à la droite ne dépend pas des points et : on construit via le graphe de

Sur la figure sont construits et point fixe de



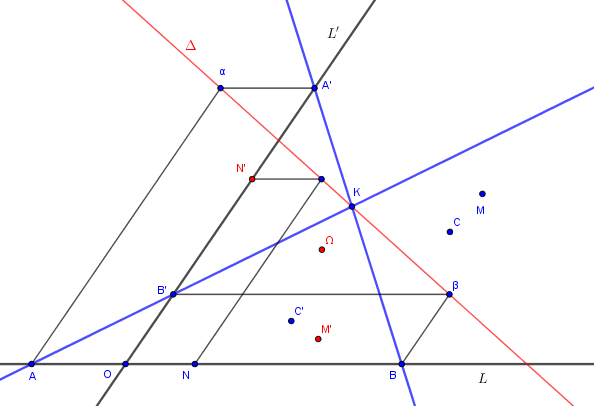
On constate que appartient à qui est aussi l'axe de l'homographie envoyant sur .

Un lien où on peut déplacer les points .

Dans le cas du problème de départ, et est une isométrie.
On peut considérer que est :

   - une similitude directe, soit une rotation.
   - ou une similitude indirecte, soit une symétrie glissée.
   - ou une autre application affine du plan ... qui dépend d'un troisième couple de points homologues.

Mais dans tous les cas la restriction qui envoie sur est toujours la même.

J'oubliais : on peut aussi se référer au théorème de Pappus :