Bonjour

Il te faut simplement connaître le volume de la boîte contenant ces boules (on peut dire par exemple que le volume de cette boîte a l'équivalent de 3 boules x 2 boules x 1 boule)et le volume total des 6 boules.
Ensuite tu fais la différence du volume de la boite et du volume total des 6 boules pour connaître le volume "non occupé" de cette boîte.

Merci beaucoup de cette aide

Bonjour,

vous croyez vraiment que cet exo est simple ????
(en une seule couche, donc le problème est équivallent à mettre des disques dans un carré)

L'arrangement optimum de 6 disques dans un carré n'a été démontré qu'en 1963 seulement.
c'est celui là :

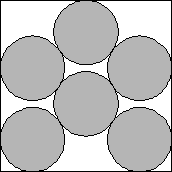
il est loin d'être trivial ! et le calcul des dimensions du carré encore moins !
(on a côté du carré = rayon (2 + 1213))

comme la boite est cubique dans l'énoncé, sa hauteur est aussi égale au coté de ce carré (et il y a une place énorme perdue au dessus des boules en une seule couche)

donc à moins qu'on définisse dans l'énoncé un autre arrangement, donc non optimal (donc les sphères peuvent bouger !! contrairement à ce qui est prétendu) c'est celui ci qu'il faudrait prendre ...

conclusion : il y a une figure avec l'énoncé qui définit comment on place les sphères. (avec une disposition calculable au niveau 3ème)

on attend cette figure ...

de toute façon, oui le volume du cube c'est a³, avec a = coté du carré de base, inconnu
et le volume des 6 boules c'est 6 fois le volume d'une boule donc 6 fois 4/3R³, diamètre = 2R = 52,4 mm
on en déduit le vide par différence certes.

mais le côté du carré ???

Complément sur les dispositions plausibles.
6 façons différentes de placer les 6 boules dans un cube en une seule couche (= 6 disques dans un carré) liste non limitative (il y a bien d'autres dispositions, dont dissymétriques)

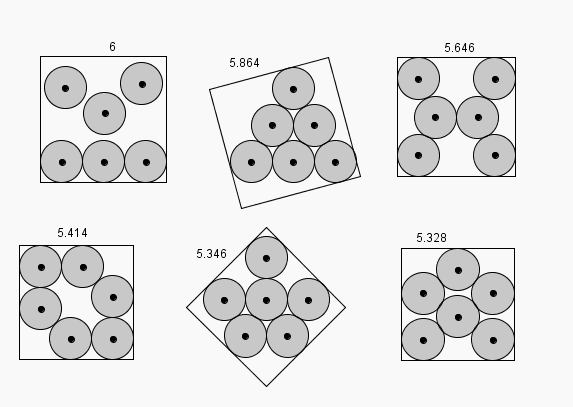
La 1ère façon "stupide" consiste à mettre une rangée de 3 boules puis les 3 autres au choix
Tout se balade dans cette boite "visiblement" trop grande
coté = 6R
c'est la boite dans laquelle on pourrait en fait mettre 9 boules (évident)

Un peu mieux est un arrangement des boules en triangle équilatéral et le plus petit carré qui contient ça.
Là aussi les boules du milieu peuvent se balader et l'arrangement n'est pas optimal.
Le coté est R(2 + sqrt(6) + sqrt(2)) = 5.863703305...

Dans l'arrangement meilleur suivant, les boules sont "coincées" on ne peut les déplacer sans les sortir de la boite.
Mais comme cet arrangement n'est toujours pas optimal, on peut les remettre avec une meilleure disposition,
dans laquelle elles "flotteraient"
Le côté est R(3 + 7) = 5.645751311...

Encore meilleur est de caler seulement 2 boules dans les coins opposés
idem, les boules sont bloquées
Le côté est R(4 + 2) = 5.414213562...

L'arrangement suivant, toujours avec les boules bloquées, donne
le coté = R(2 + (3 + 3)/2) = 5.346065215...

Enfin l'arrangement démontré optimal par Graham en 1963
avec coté = R(2 + 12/13) = 5.328201177...
(nota : errata de mon post précédent un signe de division avait sauté)

Calculs non détaillés (et de toute façon pas tous du niveau 3ème)

Il est encore moins évident de mettre six sphères en 3D (= sur plusieurs niveaux) dans un cube.