Erreur de saisie, il n'y a pas de dans la 1ère intégrale.

Bonjour,

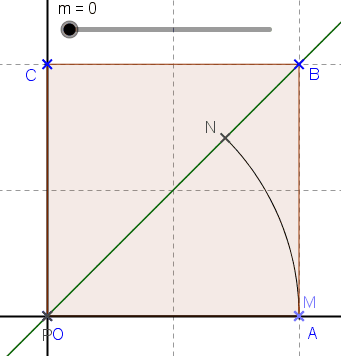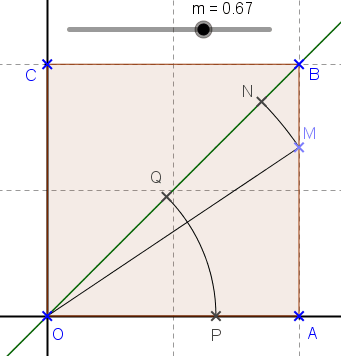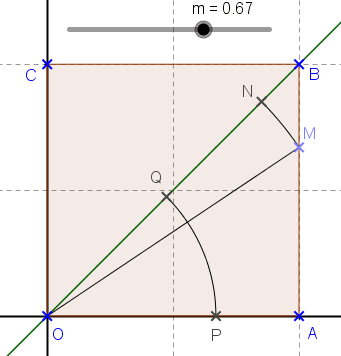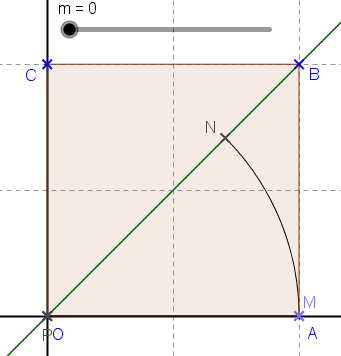
Il faut faire un dessin . Le domaine d'intégration est le carré .

Comme l'intégrale est symétrique en x et y, il suffit de la calculer sur le domaine délimité par l'axe des x et les droites y=x, et x=1 puis de multiplier par 2.

Je vous laisse en déduire les bornes en polaires.

ton changement de variables est x = r cos et y = r sin

si x et y varient entre 0 et 1, entre quoi et quoi doivent varier r et à ton avis ?

Merci beaucoup,

j'ai trouvé, pour l'exemple, et .

non si x et y varient entre 0 et 1, r = (x²+y²) varie entre 0 et 1

les cosinus et sinus doivent permettre à x et y de varier entre 0 et 1 donc varie entre 0 et /2

Je suppose qu'il multiplie le résultat par 2, comme je le lui avais suggéré.

De plus entre /4 et /2, il faudrait changer la borne supérieure de l'intégrale en r.

Oui j'ai suivi l'indication de larrech et cherché comment décrire la figure obtenue (le triangle) à l'aide de et .

Les , c'est aussi ce que j'avais fait mais ça ne donne pas le bon résultat.

Mais d'une manière plus générale, il n'y a pas de "formules" pour trouver les bornes ?

En gros si j'ai un domaine de , que je fais le changement de variable polaire comment explicite-t-on ? J'imagine qu'on ne peut pas toujours faire un dessin.

Personnellement , je ne connais pas de "formule" passe partout.
Il reste  ce que suggérait Glapion.
On ne peut pas toujours faire de dessin, non, mais une connaissance de la nature géométrique du domaine d'intégration me semble indispensable.

Merci pour vos réponses en tout cas.

Bonjour
ce que suggère Glapion va donner un quart de disque, et pas un carré, ou j'ai zappé quelque chose ? (vu l'heure c'est fort possible)

oui, à mon avis l'image du carré initial par le changement de variables est bien un quart de disque.

Oui, tu as raison, je me suis planté.

C'est dans ce que j'ai raconté le 16 à 15h08 que j'ai un peu déraillé.

salut

Mon calcul conduisait à



ce qui ne devrait pas être loin d'être la même chose

...

ouais mais je pense qu'il y a des erreurs de bornes dans la deuxième intégrale du calcul de J

et je ne vois pas d'où vient ton 1/ cos t ...



ha enfin je suis d'accord avec toi ...

Ah, oui, là c'est pile poil la même chose.

Oui je vois que j'ai raconté des bêtises. r ne varie pas entre 0 et 1 mais de 0 à 1/cos t.
pas si facile ces changements de variables polaires dans les intégrales doubles.
désolé .

no problemo ...

même un orange doit se mettre au vert parfois ...