Inscription / Connexion Nouveau Sujet
Calcul vitesse
Enoncé:
"Un avion vole horizontalement à 7840 m d'altitude, à la vitesse de 450mk/h. A la verticale d'un point A, il laisse tomber un objet. On suppose que cet objet va décrire une courbe C dans un plan vertical passant par A. (A;  ,
, ) est un repère orthonormé de ce plan comme indiqué ci-dessus (unité graphique: 1cm pour 1000m).
) est un repère orthonormé de ce plan comme indiqué ci-dessus (unité graphique: 1cm pour 1000m).
1. Courbe C
A l'instant t (en secondes), l'objet est repéré par le point M(x(t);y(t)) tel que:
x(t)=
et y(t)= -4.9t²+7840
x(t) et y(t) sont exprimés en mètres.
a) A quel instant l'objet touchera-t-il le sol?
b) En quel point l'objet touchera-t-il le sol?
c) Exprimer y en fonction de x et donner une équation de la courbe C.
d) Dans le repère (A; ,
, ), tracer la courbe C.
), tracer la courbe C.
2.Vitesse instantanée
Le vecteur-vitesse instantanée de l'objet à l'instant t est le vecteur 
 (t) de coordonnées (x'(t),y'(t)).
(t) de coordonnées (x'(t),y'(t)).
a) Déterminer le vecteur-vitesse à l'instant:
t=0 et t=40
b) Déterminer une équation de la tangente T à C au point M à l'instant t=20.
c) Tracer T sur le graphique précédent et tracer le représentant d'origine M du vecteur 10 (20). Que constate-t-on?
(20). Que constate-t-on?
d) Exprimer en fonction de t la longueur du vecteur  (t). Cette longueur est la vitesse scalaire de l'objet, elle est exprimée en m/s. Calculer cette vitesse scalaire, arrondie au dixième, à l'instant:
(t). Cette longueur est la vitesse scalaire de l'objet, elle est exprimée en m/s. Calculer cette vitesse scalaire, arrondie au dixième, à l'instant:
t=0 et t=20 et t=40"
Je pense avoir réussi à trouver les bonnes réponses jusqu'au
2.b). Pour la 2.c) Sachant que la courbe est donné par la fonction y(x)=-4,9(x/125)²+7840
que l'équation de la tangente en M si t=20 est y=-1.568x+9800
et que 10 (20)=(1250;-3920),
(20)=(1250;-3920),
J'ai tracé la tangente en M et le vecteur d'origine M sur Géogébra et je ne sais pas si je me trompe mais je ne vois pas ce que je dois constater.
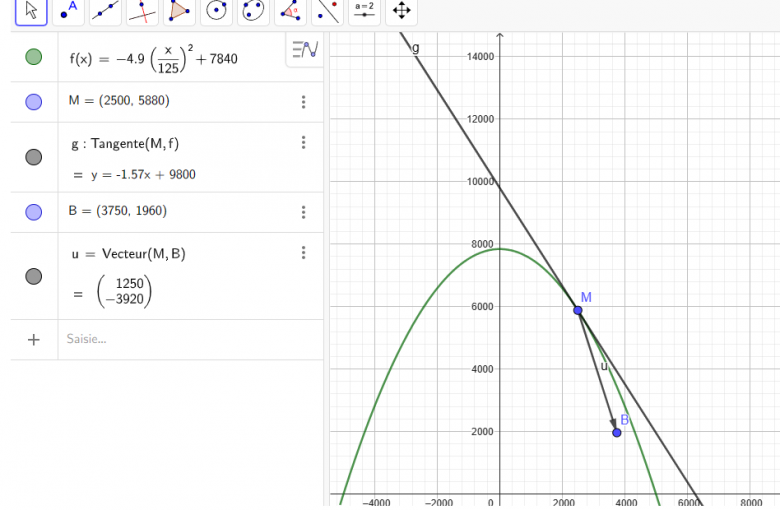
Ah oui en effet, je viens de voir mon erreur, donc ce vecteur est une portion de la tangente en M.
Je suis maintenant bloqué avec la dernière question!
ce vecteur vitesse instantanée a pour support la tangente, oui
on te demande juste de calculer le module de ce vecteur
(cours pour calculer le module d'un vecteur connaissant ses coordonnés)


