Bonjour,

Puisque X et Y sont indépendantes, tu connais la densité jointe du couple X,Y.

Il te reste à bien comprendre l'évènement U <= x (tu peux faire un dessin pour le représenter dans le quadrant positif). Ensuite, une petite intégrale à calculer.

J'ai compris pour la densité du couple (X,Y) merci

Mais j'ai un peu de mal pour me représenter U <= x
Ce que j'ai compris c'est que lorsque X>Y, alors U = 0 et lorsque X , U = X

Ne peux-tu pas représenter l'ensemble des couples (s,t) tels que (X,Y)=(s,t) entraîne U <= x  (pour x >= 0) ?

Je ne vois pas trop où vous voulez en venir ?

À répondre à la question posée.
La variable aléatoire est de la forme , où la fonction est définie par si et si . Je te propose, pour donné, de dessiner l'ensemble des couples   tels que  .
Vu que tu connais la densité jointe du couple , ça devrait t'aider à comprendre comment calculer , ce que tu cherches à faire.
Maintenant, si la voie que je te propose ne te plaît pas, tu n'es pas obligé de la suivre ...

bonjour, je ne sais pas résoudre l'exercice donc toutes les voies sont bonnes à prendre.
C'est cette phrase que je ne parviens pas à faire : dessiner l'ensemble des couples (s,t)  tels que  

Il s'agit pourtant de compréhension basique. J'ai rappelé comment on calcule u(s,t). Tu te donnes une valeur x, disons x=2 pour fixer les idées. Il s'agit alors de dessiner l'ensemble des (s,t) tels que u(s,t) <=2. Tu peux te limiter au quadrant des (s,t) avec s>=0 et t>=0, vu que X et Y ne prennent que des valeurs positives ou nulles.
Est-ce que pour s=5, t=3 on a u(s,t) <= 2 ?
Est-ce que pour s=4, t=7 on a u(s,t) <= 2 ?
Est-ce que pour s=1, t=3 on a u(s,t) <= 2 ?
Peux-tu dessiner l'ensemble des (s,t) du quadrant positif tels que u(s,t) <= 2 ?

Comme indiqué sur le sujet, je suis en reprise d'étude donc même "les choses basiques" peuvent être devenu compliqué par oublie etc .

Ce que je voulais dire en parlant de compréhension basique, c'est qu'il ne s'agit pas ici de choses "à savoir" mais de bien se représenter la situation.
Une petite erreur dans ta réponse pour le cas s=4, t=7 : on n'a pas u(s,t)=7. Peux-tu corriger ?

Ce que je te suggère de dessiner, c'est l'ensemble des valeurs de X,Y pour lesquelles on a U <=  2. L'intégration de la densité jointe de X,Y sur cet ensemble te donnera alors la probabilité que U <= 2.  Après tu pourras remplacer 2 par une valeur x quelconque, tu aras la fonction de répartition de U. C'est bien ce que tu cherches, non ?

Nos messages se sont croisés, je vois que tu as corrigé tes erreurs. Courage, tu vas bien arriver à réaliser ce qu'est l'ensemble des valeurs (s,t) de (X,Y) pour lesquelles on a U <= 2 !

Ce que je comprends pas c'est comment le dessiner, il n'y a rien d'explicite non? Car vous avez pris des cas précis s=5 et t=3..?

Oui, les cas précis étaient pour te faire comprendre comme se calcule u(s,t).

Par exemple, ne saurais-tu pas dessiner l'ensemble des couples (s,t) avec s >= 0, t >= 0 et s <= t ?
Ce que je te demande est juste un petit peu plus compliqué, mais pas beaucoup plus ...

Bonsoir à tous les deux.

Pour lytar.
Peux-tu interpréter le schéma ci-dessous ?

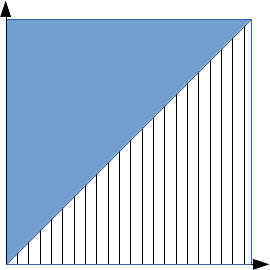
dans le cadre de la question posée par GBZM ?

Je vous avoue que je ne sais pas

Nous en revenons à la compréhension basique.
La partie coloriée en bleu sur le schéma de Verdurin représente l'ensemble des (s,t) du quadrant positif tels que s <= t. Le vois-tu ?

Non...

Vrai, tu ne vois pas qu'un point de coordonnées (s,t) est dans la partie coloriée en bleu si et seulement si s>=0 et t>=0 et s<=t ????

je suis complètement perdu, et surtout je n'arrive pas à faire le lien avec l'exercice..

Je te rappelle ça :

Pour lytar.
Je me demande si tu n'as pas oublié ce message

Euh, Verdurin, c'est .

Bien sur.

Je vous avoue que je suis un peu perdu ^^

Je n'aime pas du tout faire ça, mais je vais faire à ta place puisque tu as l'air totalement incapable de te représenter l'ensemble des valeurs de X,Y pour lesquelles on a U <=2



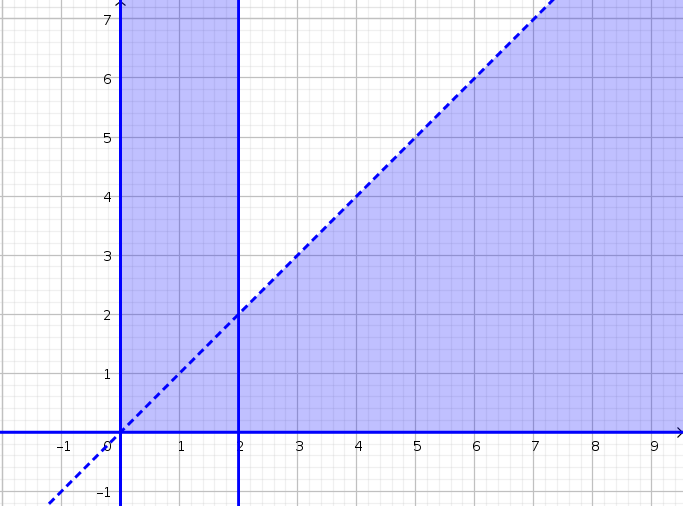
C'est l'ensemble des couples (s,t) de réels positifs ou nuls tels que s>t ou que s <=2.
L'évènement "U<=2" est la réunion disjointe de l'évènement "X<=2" et de l'évènement "X>2 et X>Y" :



La probabilité de U<=2 se calcule donc en additionnant la probabilité X<=2 et la probabilité de (X>2 et Y<X). Cette dernière probabilité se calcule en intégrant la densité jointe f_X,Y du couple (X,Y) sur l'ensemble des (s,t) tels que 2<=s et que 0<=t<=s :



Je te laisse remplacer 2 par un réel positif x quelconque et mener les calculs.

Oups, je corrige ma formule, s varie de 2 à plus l'infini :

GBZM @ 31-03-2021 à 10:43