Inscription / Connexion Nouveau Sujet
carré et bâtons
Bonjour à tous
Je pense que Imod ne m'en voudra pas d' étendre son exercice
On dispose n bâtons de longueur 1à n
on les dispose pour former des polygones réguliers de façon à ce que
les longueurs des cotés soit égales et que chaque coté doit compter un
nombre différent de bâtons.
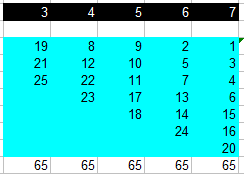
A/le carré
B/le pentagone
C/l'hexagone
Nous avons trouvé 2 solutions pour le triangle.
Amusez-vous bien (en ce temps de pluie  )
)
Bonjour Dpi
Comme tu me cites dans ton message , je me permets de te demander de préciser la question . Dans mon problème la question était de trouver la valeur minimale de n pour que la construction soit possible . Si on ne limite pas n , il y a une infinité de solutions .
Je te signale aussi que pour la valeur minimale du triangle , il y a 6 solutions .
On peut trouver intéressant de chercher toutes les solutions pour la valeur minimale mais commencer par trouver ce minimum me semble un bon début ( le reste risque d'être un travail de machine ) .
Imod
Bonjour Imod
Je reste dans le même esprit n doit être minimal pourvu qu'on respecte les conditions .
Dans le cas du carré , vu la longueur totale des bâtons il faut que leur nombre soit congru à 0 ou 7 modulo 8 . Comme chaque côté doit comporter un nombre différent de bâtons , il en faut au moins 10 . Le premier cas à considérer est n=16 .
Imod
Une particularité qui m'avait échappé , avec 16 bâtons le côté du carré doit faire 14 : il y a un gros problème et je pense qu'il se reproduira souvent ainsi que pour les autres polygones .
Imod
Nous en sommes à
2 solutions pour le carré
1 solution pou le pentagone
1solution pour l'hexagone
1 solution pour l'heptagone
Bonjour,
pour le carré verdurin a trouvé la plus petite valeur de n.
En effet, comme l'a dit imod, n doit être congru à 0 ou 7 modulo 8 et comme il y a au moins bâtons la plus petite valeur est au moins
.
Mais à partir de il ne peut pas y avoir un côté avec 2 bâtons puisque
.
Il faut donc au moins bâtons et la plus petite valeur est au moins
.
Bonsoir dpi.
Le quatrième coté est évident : c'est la somme des nombres restants.
Je conjecture qu'il y a une solution pour tous les k-gones et que presque tous les nombres n vérifiant conviennent.
Un raisonnement analogue à celui que j'ai fait pour le carré donne la plus petite valeur de n pour un pentagone, valeur qui donne bien au moins une solution :
 Cliquez pour afficher
Cliquez pour afficher>verdurin
Je parlais du détail soit pour le 4 ème coté composé de 8 bâtons :
4+6+7+8+9+10+12+13 =69
une fois connu la solution optimale 23;69 on sait qu'il y aura plusieurs détails.
>jandri
Je pense que tu propose donc 30;93
 Cliquez pour afficher
Cliquez pour afficherBonjour dpi,
tu as parfaitement raison, j'ai éliminé ce cas par erreur : j'ai écrit trop vite quels sont les n qui vérifient la condition n(n+1) multiple de 10 et je n'ai pas vu qu'il y a alors 4 cas pour la congruence modulo 10.
Merci,
J'en suis à l'heptagone ,mais il faut se dire qu'au delà les nombres
progressent très vite...
J'attends des candidats détaillés pour ceux de l'énoncé.
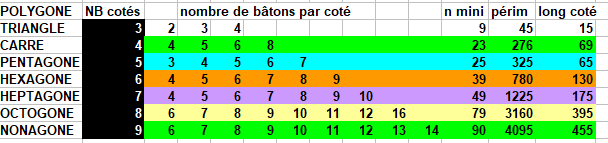
Comme l'a signalé verdurin,on doit pouvoir continuer pour tous les k-gones.
Pour ma part je m'en tiens à l'octogone 79;395 que je je vous joins:
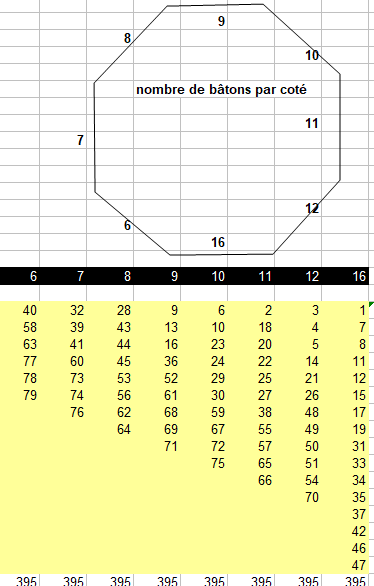
Je ne suis pas vraiment intéressé par la recherche du nombre de solutions réalisant le minimum mais celle du minimum est plutôt intéressante . La contrainte principale est car la taille de chaque côté vaut n(n+1)/2c . La contrainte sur le nombre différent de bâtons sur chaque côté n'intervient que pour les petites valeurs de n car en divisant suffisamment chaque bâton et en rassemblant les morceaux autrement la contrainte s'évanouit très vite . La conjecture de Verdurin est clairement un théorème . Pour la recherche du minimum le cadre est bien plus serré car les petits bâtons ne peuvent être utilisés qu'une seule fois pour compléter les côtés . Il n'est pas idiot de chercher le nombre minimum de bâtons pour l'hexagone , l'heptagone , … et de jeter un coup d'œil dans L'OEIS , il serait surprenant que la suite de valeurs obtenues ne soit pas déjà référencée .
Imod