Inscription / Connexion Nouveau Sujet
Centre de Gravité d'un triangle & Vecteurs
Bonjour, Bonjour !
J'ai affaire à un DM plutot compliqué, dans le sens où aucune valeur n'est précisée ! :/
Voici l'énoncé ! (J'ai réussi toutes les questions sauf deux.. )
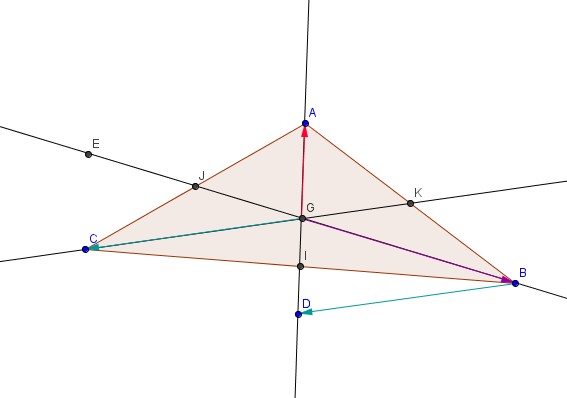
SOit un Triangle ABC quelconque et I, J, K les milieux respectifs des segments [BC], [AC] et [AB]
Soit G le centre de gravité du triangle ABC
I]Le but est de montrer que si G est le centre de gravité du triangle ABC
alors Vecteur GA + Vecteur GB + Vecteur GC = vecteur nul
1) Faire une figure (CF. Image)
2) a) Construire D tel qu Vecteur GD = Vecteur GB + Vecteur GC
b) Démontrer que D est sur la droite (AI)
3) a) Construire E symétrique de G par rapport à I
b) Démontrer que EAGC et EDBA sont des parallèlogrammes. (1° question que je n'ai aps réussie)
4) a) Déterminer alors vecteur GA + Vecteur GD
b) En déduire que vecteur GA + vecteur GB + vecteur GC = vecteur nul
II] Réciproquement le but est de montrer que si Vecteur GA + Vecteur GB + Vecteur GC = vecteur nul
alors G est le centre de gravité du triangle ABC
1) Soit M un point du plan. Démontrer que Vecteur MA + Mecteur MB + Vecteur MC = 3 Vecteur MG
2) Soit H un point du plan tel que Vecteur HA + Vecteur HB + Vecteur HC = 0, Démontrer que H = G (2° question que je n'ai pas réussie)
REPONSES :
I] 2) * On sait que Vecteur GD = Vecteur GB + Vecteur GC, On en déduit que Vecteur GC = Vecteur BD
Donc GBDC Parallélogramme
* I est le milieu de [BC], diagonale de GBDC.
Or un Parallélogramme a ses diagonales qui se coupent en leur milieu.
Donc I Milieu [BC] et I milieu de [GD]
Donc G appartient à (AI)
3) * On sait que J milieu [AC] et J milieu [EG](car E symétrique de G par rapport à J] et EAGC quadrilatère.
Or si un quadrilatère a ses diagonales qui se coupent en leur milieu, c'est un parallélogramme.
DOnc : EAGC prallélogramme.
* Je ne vois pas comment procéder pour EDBA...
4) a) Vecteur GA + Vecteur GD = Vecteur GG = Vecteur Nul
b) Vecteur GA + Vecteur GD = Vecteur Nul
Vecteur GA + ( Vecteur GB + Vecteur GC) = Vecteur Nul
II] 1) Vecteur MA + Vecteur MB + Vecteur MC
= (Vecteur MG + Vecteur GA) + (Vecteur MG + Vecteur GB) + (Vecteur MG + Vecteur GC)
= 3 Vecteur MG + Vecteur GA + VEcteur GB + VEcteur GC
On sait que Vecteur GA + Vecteur GB + Vecteur GC = Vecteur nul
Donc Vecteur MA + Mecteur MB + Vecteur MC = 3 Vecteur MG
2) Je pense qu'il faut procéder de la meme manière mais je ne ne vois pas...
%Merci de votre aide, d'avance !
Mes réponses sont elles justes ? 
AMicalement Lamolle 2
Bonjour Lamolle,
2b) Il serait plus pertinent de terminer ainsi : " ... I milieu de [GD] . Donc D appartient à (GI), et donc à (AI) !
3) Je suppose que E est le symétrique de G par rapport à J (et non I)
3b) Pour EDBA, regarde simplement les vecteurs et
, en tenant compte de ce que tu viens de démontrer.
II,2) C'est simple : si d'une part et
d'autre part, c'est que
et donc H=G.
Mais la démonstration n'est correcte que si on l'articule correctement :
- soit G le centre de gravité (au sens point de concours des médianes) de ABC ; on a montré (partie I) qu'il vérifie l'égalité
- je montre (partie II) que si un autre point H vérifient l'égalité , alors il est confondu avec G, le centre de gravité
- conclusion : il n'y a qu'un point qui vérifie , et ce point est G.
Il aurait beaucoup mieux valu rédiger le début de la deuxième partie ainsi : "Réciproquement le but est de montrer que si , alors H est le centre de gravité G du triangle ABC .
NB général : quand j'étais à l'école, on avait l'habitude de nommer les sommets d'un polygone dans le sens inverse des aiguilles d'une montre, qui est le sens habituel d'orientation du plan (= sens "direct" en trigonométrie, par exemple).
Après recherche, j'ai réussi à trouver les réponses aux questions qui me posaient problème hier soir.
J'en suis venue aux mêmes résultats (Normal ^^) Par contre ma rédaction n'était pas très bonne. Merci de m'avoir aidé sur ce point.
Pour ce qui est du N.B, il est vrai que j'écris habituellement dans le sens inverse des aiguilles d'une montre. Sur le logiciel, j'ai fait dans l'autre sens. Je prendrais garde à écrire dans le sens conventionnel sur ma copie.
Merci de toutes ces remarques, et de m'avoir aidé .
Bonne journée. 


