Inscription / Connexion Nouveau Sujet
Centre de l'homothétie
Bonjour
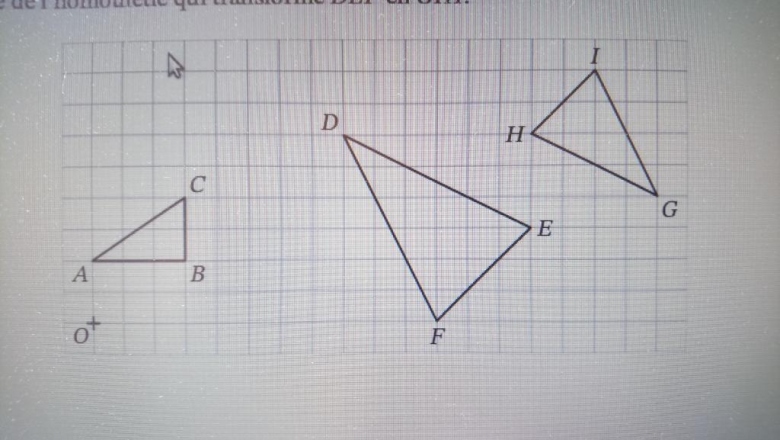
Comment construire le centre de l'homothétie qui transforme DEF en GHI.
J'ai tracé les parallèles (DI) et (EG) et les secantes (DG) et (EI) S leur point d'intersection
Est ce normal que HS et E ne sont pas alignés
Oui et...?
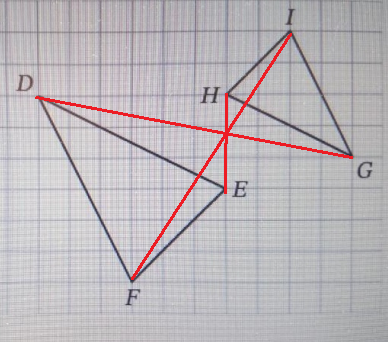
Si je trace ces 3 droites( D G) , (E H) et( F I) elles devraient se couper dans le même point
Non ?
C'est ce que j'ai fait et ça ne marche pas.
Moi j'avais tracé (EG) car elle est parallèle à (DI) et donc on peut appliquer Thales
Dans le quadrilatère DIEG
- tu prétends que tu traces ( D G) , (E H) et (F I) et tu en traces d'autres à la place !!!??? (EI)
- tes "parallèles" ne riment simplement à rien du tout
les parallèles dans une homothétie ce sont des droites homologues
une droite de une des figures (DEF) homologue d'une droite de l'autre figure (GHI)
(DE) // (GH), (EF)//(HI) et (DF)//(GI)
pas des droites qui relient un point de l'une (E) avec un point de l'autre (G) !!
la droite (EG) n'a absolument aucun sens dans cette homothétie.
- et de toute façon ces parallèles n'interviennent pas du tout dans la construction du centre d'homothétie
alors comment repérer les côtés homologues?
moi j'essayais de construire un schéma ou je pourrais appliquer Thalès.
si ma méthode ne rime à rien du tout ce serait cool que tu expliques la bonne.
Bonjour pseudau
vu la tête de tes deux triangles, je crois que tu es d'accord pour dire que D et G sont homologues par l'homothétie
donc tu sais que le centre d'homothétie (que je vais appeler K ) va appartenir à la droite (DG)
ensuite tu as le choix pour la correspondance pour les points F et E
mais tu ne dois pas oublier que le centre d'homothétie K appartient toujours aux droites "un point-son point homologue"
donc tu n'as pas trop le choix...tu testes, un choix ne va pas, l'autre va

pour le choix des sommets homologues on peut faire intervenir des parallèles mais c'est comme j'ai dit ;
une droite de DEF
parallèle à
une droite de GHI
pas une droite reliant un point de l'une à un point de l'autre !!
ainsi si on cherche une droite de GHI qui serait parallèle à la droite (DE) de DEF
on voit immédiatement que c'est (GH) et pas (GI) donc H est l'homologue de E
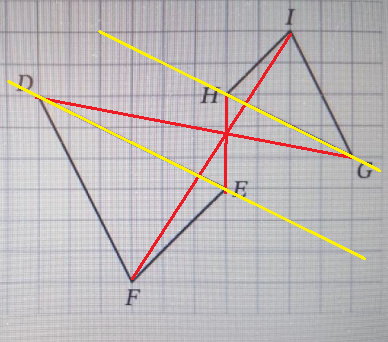
ensuite il suffit de faire vraiment ce qu'on dit soi même que l'on fait, et pas de faire autre chose que ce qu'on dit !
si tu dis que tu traces la droite (FI) et que en fait tu traces la droite (EI) ton tracé ne correspond pas à ce que tu dis que tu fais !!!