Inscription / Connexion Nouveau Sujet
Challenge n°121

Bonsoir, nouvelle énigme pour vous :
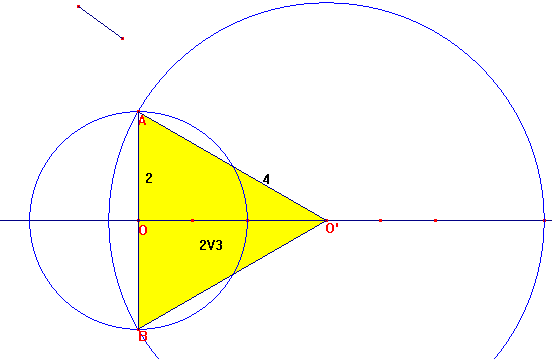
Soit C1 et C2, deux cercles sécants (non tangents), dont les deux points d'intersection sont nommés A et B. C1 est un cercle de centre O et de rayon 2, et C2 est un cercle de centre O' et de rayon 4. On nomme d la distance OO'. Quelle valeur exacte de d doit-on prendre pour obtenir une surface maximale de OAO'B ?
Bonne chance à tous 
 Aaaaargh Sof m'a grillée...
Aaaaargh Sof m'a grillée...
Pour avoir l'aire maximale, il faut que OAO' soit un angle droit. Donc avec pythagore OO' =  20
20
c'est à dire d= 2 5
5
 Le quadrilatère OAO'B est constitué de 2 triangles éguax (OAO' et OBO') dont l'aire est donnée par la formule de Héron:
Le quadrilatère OAO'B est constitué de 2 triangles éguax (OAO' et OBO') dont l'aire est donnée par la formule de Héron:
Il faut donc rendre maximum S2 = [(6+d)/2] [(6+d)/2 - 2] [(6+d)/2 - 4] [(6+d)/2 -d]
Soit S2 =(1/16)*(36-d2)(d2-4)
La dérivée de cette fonction s'annule pour d = 20.
20.
L'aire du quadrilatère OAO'B est donc maximale et égale à 4 pour d = 20
20  4,47.
4,47.
Nota : on notera que pour cette valeur OA (resp. OB) est perpendiculaire à O'A (resp. O'B).
 L'aire de OAO'B est S=RR'sin(OAO') qui est maximum si les cercles sont orthogonaux auquel cas d^2=R^2+R'^2, d^2=4+16=20
L'aire de OAO'B est S=RR'sin(OAO') qui est maximum si les cercles sont orthogonaux auquel cas d^2=R^2+R'^2, d^2=4+16=20
d=V20=2V5=4,472 si V est la notation de la racine carrée
 Si je note h la hauteur du triangle OAO' issue de O :
Si je note h la hauteur du triangle OAO' issue de O :
L'aire de OAO' vaut alors 4h/2 et l'aire de OAO'B le double, soit 4.h
Il faut donc maximiser h, ce qui se produit quand l'angle OAO' est droit.
Alors, h=2 et d2 = 22 + 42 = 20 soit d = √20
Sinon, on peut calculer l'aire de OAO'B en fonction de d :
√(10d2-d4/4-36)
L'aire est maximale quand sa dérivée par rapport à d s'annule, soit pour d = √20,
ce qui donne des angles droits en A et B et une aire de 8.
Réponse : d = √20
 bonjour,
bonjour,
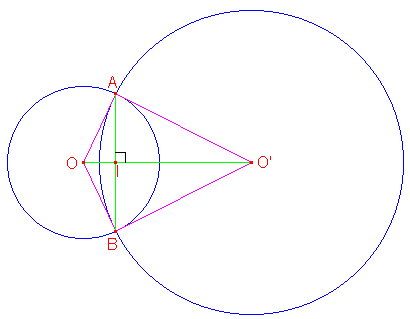
A est le symmétrique de B par rapport à (OO'), ainsi, l'aire du triangle OO'A égale l'aire du triangle OO'B. Donc aire(OAO'B) = 2 * aire(OO'A)
Alors, trouver d pour que l'aire OAO'B soit maximale revient à trouver d pour que l'aire du triangle OO'A soit maximale
Si on note H le projeté de O sur (AO') et h la distance OH (voir dessin)
Aire (OO'A)=4*h/2
si on veut trouver l'aire maximale, cela revient de nouveau à trouver d tel que h soit maximal
h sera maximal si le point A est en H. ainsi, h=OA=2
si A est en H, alors le triangle OO'A est rectangle en A
ainsi, d²=4²+2²
=> d=racine(20)
d=2*racine(5)


 L'aire
L'aire de
;
;
Alors
En annulant la dérivée ,on trouve :
 Bonsoir,
Bonsoir,
Le problème est assez semblable au Challenge n°121.
On peut invoquer la trigo ou même faire bourrin (d² est le maximum du polynôme -x²+40x-144)...
Je propose une autre solution.
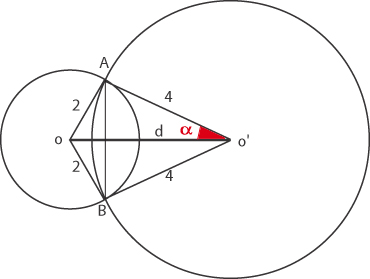
Le quadrilatère OAO'B est un cerf-volant (nom officiel de cette figure fraîchement apparue cette année dans les programmes).
Parfaitement symétrique par rapport à sa diagonale [OO'], son aire vaut deux fois celle du triangle OAO'.
Reste à maximiser cette aire sous les contraintes OA=2 et O'A=4.
En considérant [OA] fixé, l'aire du triangle OAO' vaut OAh où h est la hauteur issue de O'.
Or cette hauteur comprise entre 0 et 4 est maximale si et seulement si h=AO'=4. Au passage, cette aire vaut 8.
L'aire maximale est donc atteinte si et seulement si le triangle OAO' est rectangle en A.
Reste à appliquer le théorème de Pythagore dans le triangle OAO' rectangle en A: OO'²=OA²+AO'²=2²+4²=20. D'où OO'=
Conclusion:
Merci, puisea, pour cette avalanche d'énigmes.
 J'ajoute à la figure le système d'axes
J'ajoute à la figure le système d'axes direct, où
.
On a alors et
.
Je vais considérer le point d'intersection (x, y) des eux cercles qui se trouve dans le premier quadrant (qui a donc ses coordonnées positives).
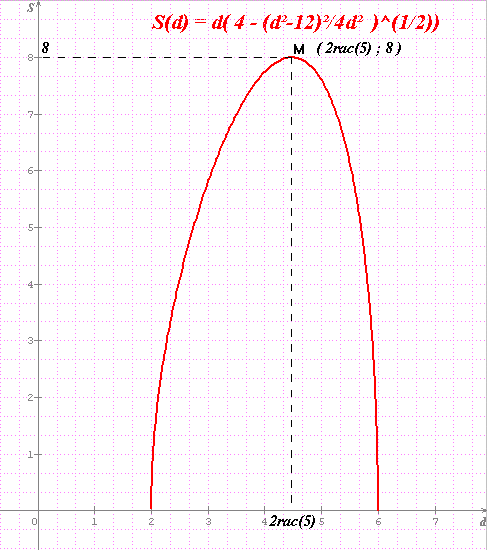
Alors l'aire de OAO'B vaut : A = d×y.
Avec, après calculs, .
Je vais chercher quand la dérivée de l'expression qui se trouve dans la racine s'annule :
.
On a d compris entre 2 et 6, donc le maximum est atteint pour , c'est-à-dire
.


 Bonjour,
Bonjour,
Réponse proposée : d=2V5 = racine(20) qui fournit une surface maximale de valeur 8 unités d'aire
Merci pour cette jolie énigme,
Philoux
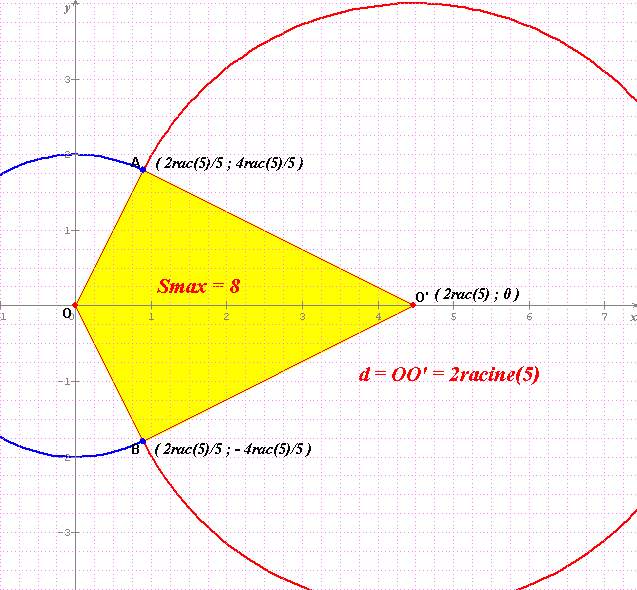


 Sauf erreur de calcul (dont je suis un spécialiste) je trouve d=
Sauf erreur de calcul (dont je suis un spécialiste) je trouve d= 20 = 2
20 = 2 5
5


la valeur exacte de d est racine carrée de 20.

Il suffit d'avoir OA perpendiculaire à O'A.Je crois que Puisea aime bien les perpendiculaires ... 


 Salut,
Salut,
Je trouve après m'etre battu avec une derivee enorme, OO'=2 5.
5.
Merci pour l'énigme.
 pour avoir une surface maximale de OAO'B, la distance d doit etre égale à (4 racine de 3) sur 3
pour avoir une surface maximale de OAO'B, la distance d doit etre égale à (4 racine de 3) sur 3
d= (4V3)/3
je ne sais pas comment faire p mettre un radical...
:s
Nombre de participations : 0
Temps de réponse moyen : 11:52:05.