Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Continuité

Posté par
Theo92 20-03-21 à 00:21

Bonjour,

on se place sur E l'ensemble des fonctions continues sur  [1, + \infty[  à support compact. On le munit des normes usuelles1,...p,....\infty.
Pour  \alpha \in \mathbb{R},  on définit    l_{\alpha} : E \longrightarrow \mathbb{C}  par  f \mapsto \int_{1}^{+\infty}f(x)x^{\alpha}dx

1)J'ai montré que  l_{\alpha}   est linéaire.
On demande de montrer qu'elle est bien définie.
f est continue, à support compact donc bornée et intégrable, de signe quelconque.
x^{\alpha}  est intégrable, positive.
l_{\alpha}  est bien définie si  \int_{1}^{+\infty} \lvert f(x)x^{\alpha}\rvert dx < +\infty,  soit dans ce cas si   \int_{1}^{+\infty}\lvert f(x)\rvert x^{\alpha}dx < +\infty

Je ne vois pas comment montrer que l est bien définie?????

2) on demande de donner une CNS sur  \alpha  pour que  l_{\alpha}  soit continue sur  (E, \lVert.\rVert_1)  puis  (E, \lVert.\rVert_{\infty})  et enfin  (E,\lVert.\rVert_q)
Il faut montrer qu'il existe M tel que  \forall x \in E, \lVert l_{\alpha}(f)\rVert\leq M \times\lVert f\rVert_{1, .. q, .. \infty} ?

Je ne vois pas quelle est la norme de  l_{\alpha}(f)  ?????

Je vous remercie par avance pour votre aide.

Posté par
carpediemre : Continuité 20-03-21 à 09:15

salut

que signifie "être à support compact" ?

Posté par
DOMOREAContinuité 20-03-21 à 09:52

bonjour,

Citation :
Je ne vois pas quelle est la norme de l_{\alpha}(f)


l_{\alpha}(f) est un complexe

D'après ton texte et f est une fonction complexe de variable réelle

De plus f est à support compact sur [1,+\infty[ \subset \mathbb{R}

les normes ||.||_1  ;||.||_q   ;||.||_{\infty} sont des normes sur E

Posté par
etniopalre : Continuité 20-03-21 à 09:55

   Bonjour  Theo92
     Ici , montrer que  pour tout a , la est " bien définie "  , consiste à vérifier que  , pour toute f : [1 , +[ continue à support compact  , t taf(t) est intégrable   sur  [1 , +[  .


Posté par
DOMOREAContinuité 20-03-21 à 10:30

remarquer que :x^{\alpha}\leq max(1,(maxsupp(f))^{\alpha})

Posté par
Theo92re : Continuité 20-03-21 à 11:36

Bonjour et merci à toutes et tous.

Pour Domorea : ce que je n'ai pas saisi, c'est ce sur quoi est définie la fonction  x^{\alpha}.
Est-ce sur l'intervalle  [1, +\infty[?
Ou bien sur le même support que f, soit un compact, et auquel cas,  la fonction puissance est bien bornée, et  l_{\alpha} bien définie car intégrable. A vous lire, ce serait donc ainsi qu'il faut comprendre l'énoncé.

Je vous remercie pour votre réponse.

Posté par
Theo92re : Continuité 20-03-21 à 11:37

Pardon.
C'est évident, puisque en dehors de ce compact, f est nulle......

Posté par
carpediemre : Continuité 20-03-21 à 11:40

et voila ...

Posté par
Theo92re : Continuité 20-03-21 à 12:26

Merci beaucoup.
Pour la suite,  l_{\alpha}  est continue sur  (E, \lVert.\rVert_1)  s'il existe une constante M telle que  \lVert l_{\alpha}(f)\rVert_\mathbb{C} \leq M\times \lVert f\rVert_1  
soit que  \lVert\int_{1}^{+\infty} f(x)x^{\alpha} dx\rVert_\mathbb{C} \leq M\times  \int_{1}^{+\infty} \lvert f(x)\rvert dx  
Que dois-je prendre pour  \lVert.\rVert_\mathbb{C}  pour traiter les différents cas de continuité sur les espaces  (E,\lVert.\rVert_1,....q,.....\infty ?????

Posté par
Theo92re : Continuité 20-03-21 à 12:37

Le module car c'est un complexe.
on obtient donc  \lvert \int_{1}^{+\infty} f(x)x^{\alpha} dx \rvert \leq M \times \int_{1}^{+\infty} \lvert f(x)\rvert dx

soit   \int_{1}^{+\infty} \lvert f(x)\rvert x^{\alpha} dx \leq M \times \int_{1}^{+\infty} \lvert f(x)\rvert dx

Comment obtient-on la condition sur  \alpha ??

Posté par
carpediemre : Continuité 20-03-21 à 12:43

tu sais que f est continue sur un compact : donc il existe m > 1 tel que x > m => |f(x)| = 0

donc |f(x) x^k| < m^k|f(x)|

(je mets k pour l'exposant

Posté par
Theo92re : Continuité 20-03-21 à 13:07

En reprenant la notation précédente, on obtient que la CNS sur  \alpha  est qu'il est tel que

(max(supp(f)))^{\alpha} \leq M

sans avoir à déterminer M (ce n'est pas demandé)

Posté par
carpediemre : Continuité 20-03-21 à 13:15

déjà il serait bien de voir que \int_1^{+\infty} f(x)x^kdx = \int_1^m f(x)x^kdx

puisque f est à support compact ...

tu peux alors répondre proprement aux questions ...

Posté par
carpediemre : Continuité 20-03-21 à 13:15

bien entendu m dépend de f ...

Posté par
Theo92re : Continuité 20-03-21 à 13:43

Merci à nouveau.

Sur  (E,\lVert.\rVert_{\infty}) on obtient la continuité si  \int_{1}^{max(supp(f))} \lvert f(x) \rvert x^{\alpha} dx \leq sup_{x \in [1,max(supp(f))]} \lvert f(x) \rvert .

là je ne vois pas du tout ce que peut être  alpha.

Posté par
carpediemre : Continuité 20-03-21 à 13:55

soit z = I_k(f)

l'application est linéaire donc il suffit de montrer la continuité en 0

dire que I_k est continue (en 0) pour la norme 1 signifie que : ||f||_1 \to 0 \Longrightarrow z \to 0

puisque I_k(0) = 0

Posté par
Theo92re : Continuité 20-03-21 à 14:07

Oui, mais on demande une condition nécessaire et suffisante sur alpha pour que  l_{\alpha}  soit continue, donc j'ai pris la majoration par un M>0

on demande la continuité sur E pour la norme uniforme, et ensuite pour finir, une CNS sur le couple  (\alpha, q)  pour que l soit continue sur  (E,\lvert.\rVert_q  en calculant cette fois la norme d'opérateur pour ces couples.

Voilà pourquoi j'ai choisi comme ça.

Je bloque sur la continuité pour la norme uniforme.
Je démarre pour la norme q.....

Posté par
Theo92re : Continuité 20-03-21 à 14:38

Ce que j'obtiens :

sur  (E,\lVert.\rVert_{\infty}),  l_{\alpha}  continue ssi  avec m=max(supp(f))  \int_{1}^{m}\lvert f(x)\rvert x^{\alpha} dx \leq M \times sup_{x \in [1,m]} \lvert f(x)\rvert    d'où une CNS sur alpha ?

sur  (E,\lVert.\rVert_q),  l_{\alpha}  continue ssi  avec m=max(supp(f))  \int_{1}^{m}\lvert f(x)\rvert x^{\alpha} dx \leq M \times (\int_{1}^{m}\lvert f(x)\rvert^q dx)^\frac{1}{q}   d'où la CNS  sur (alpha,q) ???

Il restera à calculer la norme de  l_{\alpha}

Posté par
Theo92re : Continuité 20-03-21 à 16:07

Est-ce que je suis dans la bonne direction?
Auriez-vous une piste pour calculer les alpha et les (alpha,q)?
Merci par avance.

Posté par
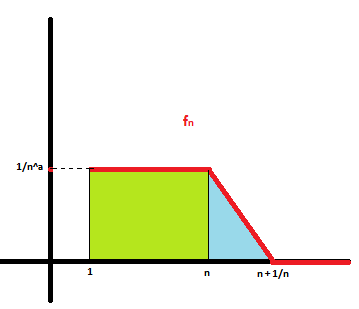
elhor_abdelali Correcteurre : Continuité 21-03-21 à 01:00

Bonsoir

\Large \boxed{2} CNS sur \alpha~ pour la continuité de \Large \boxed{~\ell_{\alpha}:\left(E,||.||_1\right)\to\mathbb C}

Condition nécessaire

Supposons \Large \boxed{~\ell_{\alpha}:\left(E,||.||_1\right)\to\mathbb C} continue et soit la suite de fonctions \left(f_n\right)_{n\geqslant1} définie par :

\Large \boxed{f_n(x)=\left\lbrace\begin{array}l \frac{1}{n^a}~,~1\leqslant x\leqslant n \\ 0~,~x\geqslant n+\frac{1}{n} \\ f~affine~sur~[n,n+\frac{1}{n}] \end{array}} où a est un réel arbitraire strictement supérieur à 1

en s'aidant d'un petit dessin, on voit facilement que f_n\in E pour tout n\geqslant1 et que ||f_n||_1=\frac{n-1}{n^a}+\frac{1}{2n^{a+1}}\to0

la continuité de \ell_{\alpha} implique donc que \ell_{\alpha}(f_n)\to0

et comme \Large \boxed{|\ell_{\alpha}(f_n)|\geqslant\int_1^n\frac{x^{\alpha}}{n^a}dx=\left\lbrace\begin{array}l \frac{\ln(n)}{n^a}~,~\alpha=-1 \\ \frac{n^{\alpha+1}-1}{(\alpha+1)n^a}~,~\alpha\neq-1 \end{array}} on voit que \Large \boxed{\alpha<a-1}

d'où la condition nécessaire \Large \red\boxed{\alpha\leqslant0} sauf erreur bien entendu

Posté par
elhor_abdelali Correcteurre : Continuité 21-03-21 à 01:31

Condition suffisante

Supposons \Large \blue\boxed{\alpha\leqslant0}, et soit f\in E

il est alors clair que \Large \boxed{|\ell_{\alpha}(f)|\leqslant\int_1^{+\infty}|f(x)|x^{\alpha}dx\leqslant\int_1^{+\infty}|f(x)|dx=||f||_1}

Posté par
elhor_abdelali Correcteurre : Continuité 21-03-21 à 02:17

CNS sur \alpha~ pour la continuité de \Large \boxed{~\ell_{\alpha}:\left(E,||.||_{\infty}\right)\to\mathbb C}

Condition nécessaire

Supposons \Large \boxed{~\ell_{\alpha}:\left(E,||.||_{\infty}\right)\to\mathbb C} continue et soit la suite de fonctions \left(f_n\right)_{n\geqslant1} définie par :

\Large \boxed{f_n(x)=\left\lbrace\begin{array}l \frac{1}{n^a}~,~1\leqslant x\leqslant n \\ 0~,~x\geqslant n+\frac{1}{n} \\ f_n~~affine~sur~[n,n+\frac{1}{n}] \end{array}} où a est un réel arbitraire strictement supérieur à 0

en s'aidant d'un petit dessin, on voit facilement que f_n\in E pour tout n\geqslant1 et que ||f_n||_{\infty}=\frac{1}{n^a}\to0

la continuité de \ell_{\alpha} implique donc que \ell_{\alpha}(f_n)\to0

et comme \Large \boxed{|\ell_{\alpha}(f_n)|\geqslant\int_1^n\frac{x^{\alpha}}{n^a}dx=\left\lbrace\begin{array}l \frac{\ln(n)}{n^a}~,~\alpha=-1 \\ \frac{n^{\alpha+1}-1}{(\alpha+1)n^a}~,~\alpha\neq-1 \end{array}} on voit que \Large \boxed{\alpha<a-1}

d'où la condition nécessaire \Large \red\boxed{\alpha\leqslant-1}


\to Theo92 je te laisse constater que \ell_{-1} n'est pas continue sur \left(E,||.||_{\infty}\right) en considérant par exemple la suite de fonctions \left(g_n\right)_{n\geqslant1} :

\Large \boxed{g_n(x)=\left\lbrace\begin{array}l 1~,~1\leqslant x\leqslant n \\ 0~,~x\geqslant n+\frac{1}{n} \\ g_n~~affine~sur~[n,n+\frac{1}{n}] \end{array}} sauf erreur bien entendu

Posté par
elhor_abdelali Correcteurre : Continuité 21-03-21 à 02:22

Condition suffisante

Supposons \Large \blue\boxed{\alpha<-1}, et soit f\in E

il est alors clair que \Large \boxed{|\ell_{\alpha}(f)|\leqslant\int_1^{+\infty}|f(x)|x^{\alpha}dx\leqslant||f||_{\infty}\int_1^{+\infty}x^{\alpha}dx=\frac{||f||_{\infty}}{-(\alpha+1)}} sauf erreur bien entendu

Posté par
elhor_abdelali Correcteurre : Continuité 21-03-21 à 02:49

Pour la continuité de \Large \boxed{~\ell_{\alpha}:\left(E,||.||_q\right)\to\mathbb C~~,~~1<q<\infty}, une condition suffisante est donnée par l'inégalité de HÖLDER :

à savoir : \Large \boxed{\forall f\in E~~,~~|\ell_{\alpha}(f)|=\left|\int_1^{+\infty}f(x)x^{\alpha}dx\right|\leqslant\left(\int_1^{+\infty}|f(x)|^qdx\right)^{\frac{1}{q}}\left(\int_1^{+\infty}|x^{\alpha}|^pdx\right)^{\frac{1}{p}}}


où p est l'exposant conjugué de q : \Large \boxed{\frac{1}{p}+\frac{1}{q}=1~~,~~p=\frac{q}{q-1}}


on trouve donc comme condition suffisante : \Large \red\boxed{\alpha<-~\frac{q-1}{q}}


\to Theo92, je te laisse examiner la nécessité sauf erreur de ma part bien entendu

Posté par
Theo92re : Continuité 25-03-21 à 19:38

Bonsoir,
je vous prie de bien vouloir pardonner le délai qu'il m'a fallu pour vous remercier sincèrement. J'ai été éloigné durant quelques jours, sans pouvoir travailler. Je me replonge dans l'exercice selon vos indications, tout en vous adressant à nouveau ma gratitude pour votre "longue" et complète explication.
Je ne manquerai pas de revenir vers vous si des points sont toujours délicats pour moi.

Posté par
elhor_abdelali Correcteurre : Continuité 25-03-21 à 19:51

De rien Theo92 c'est un plaisir

Posté par
Theo92re : Continuité 26-03-21 à 02:50

Bonsoir elhor_abdelali.
J'ai quelques points qui restent obscurs.

1) Je ne parviens pas à calculer  \lVert f\rVert_{1} = \int_{1}^{n} \frac{1}{x^{a}}dx   ????  je ne parviens pas à votre résultat.

2) Est-ce qu'en définissant  f_n  de la sorte, cela a un niveau de généralité tel que cela fonctionne pour définir la CNS sur  \alpha  et la continuité, ou bien en imaginant une autre suite de E convergeant vers  0_{E},  on obtient alors une CNS différente?

3) Pourquoi et comment s'impose le choix de  a  arbitraire selon les normes 1 et infinie, sachant que ce choix détermine par la suite la valeur de  \alpha

Merci par avance.

Posté par
Theo92re : Continuité 26-03-21 à 03:28

J'ai vu pour la 3 car  f_n  est une fonction de Riemann intégrable ssi  a>1 pour la norme 1. OK pour la norme infinie.

je bloque sur la 1 et la 2

Posté par
elhor_abdelali Correcteurre : Continuité 26-03-21 à 23:22

Bonsoir Theo92


Citation :
2) Est-ce qu'en définissant f_n de la sorte, cela a un niveau de généralité tel que cela fonctionne pour définir la CNS sur \alpha et la continuité, ou bien en imaginant une autre suite de E convergeant vers 0_{E}, on obtient alors une CNS différente?

3) Pourquoi et comment s'impose le choix de a arbitraire selon les normes 1 et infinie, sachant que ce choix détermine par la suite la valeur de \alpha



\Large \boxed{2)} En fait il existe une infinité de suites (f_n) de E convergeant vers 0_E que ce soit pour la norme ||.||_1 , ||.||_q ou ||.||_{\infty}

et il me fallait choisir des suites (f_n) qui me donneraient des conditions nécessaires optimales c'est à dire qui seraient aussi suffisantes.

Mais une fois qu'on prouve que la condition nécessaire trouvée à l'aide d'une certaine suite (f_n) est aussi suffisante,

la CNS alors déterminée devient indépendante du choix de (f_n).


\Large \boxed{3)} Le choix précis des suites (f_n) pour chaque norme m'est venue après plusieurs essais qui m'ont donné des conditions nécessaires non optimales (ie non suffisantes)

d'où l'idée d'introduire le paramètre réel a pour aboutir à cette optimalité.

Posté par
elhor_abdelali Correcteurre : Continuité 27-03-21 à 00:05

\Large \boxed{1)} \Large \boxed{f_n(x)=\left\lbrace\begin{array}l \frac{1}{n^a}~,~1\leqslant x\leqslant n \\ 0~,~x\geqslant n+\frac{1}{n} \\ f~affine~sur~[n,n+\frac{1}{n}] \end{array}} où a est un réel arbitraire strictement supérieur à 1



le dessin montre clairement que \Large \boxed{||f_n||_1=\int_1^nf_n(x)dx~+~\int_n^{n+\frac{1}{n}}f_n(x)dx=\frac{n-1}{n^a}~+~\frac{1}{2}\times\frac{1}{n}\times\frac{1}{n^a}}


la condition a>1 est nécessaire pou avoir \lim_n ||f_n||_1=0

Continuité


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !