Niveau LicenceMaths 2e/3e a

convergence

Posté par
mathmusic 21-08-25 à 20:14

Bonsoir,
Je cherche à déterminer la convergence ou non de cette série.

Pour l'instant , je sais que si la somme Un converge alors Un -> 0.
Je pensais à exploiter ce qu'il y a dans la somme en essayant de l'encadrant par une expression.
On voit que Un =1/ln(n)^p > 0 pour n >=2.
Je ne vois pas comment avancer .

Avez vous des pistes à privilégier ?
Mercii

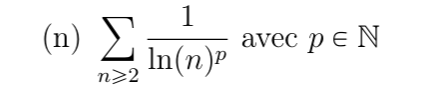
convergence

Posté par re : convergence 21-08-25 à 21:25

Bonsoir,

Soit $p\in\mathbb{N}$ . Au voisinage de $+\infty$ , qui de la fonction $x\longmapsto \ln (x)^p$ ou de la fonction identité te semble "être la plus forte" ?

Penser alors à comparer $\dfrac{1}{\ln(n)^p}$ et $\dfrac{1}{n}$ lorsque $n$ est suffisamment grand...

Quelle est la nature de la série $\underset{n\geqslant 1}{\sum}\dfrac{1}{n}$ ?

Posté par re : convergence 21-08-25 à 22:00

Bonsoir , Merci de votre temps !
La fonction identité semble la croitre beaucoup plus rapidement que la fonction donnée.
On peut donc établir cette relation ?  pour n suffisamment grand :
      n > ln(n)^p
     1/ n < 1 / ln(n)^p

On somme et on sait que la série harmonique somme (1/n) diverge.
Or je voudrais encadrer de l'autre côté pour en déduire que par comparaison notre série somme(1/ln(n)^p) diverge également .
Comment faire ?

Posté par re : convergence 21-08-25 à 23:20

Bonsoir

Pas besoin d'encadrer de l'autre côté pour montrer que ça diverge

Si c'est plus grand qu'un terme général de série divergente, et que ce sont des séries de terme positif, alors la série diverge

Posté par re : convergence 21-08-25 à 23:27

Bonsoir,

Super ! Merci beaucoup !

Bonne soirée

Posté par re : convergence 22-08-25 à 11:50

mathmusic @ 21-08-2025 à 22:00

Bonsoir , Merci de votre temps !
La fonction identité semble la croitre beaucoup plus rapidement que la fonction donnée.
On peut donc établir cette relation ?  pour n suffisamment grand :
      n > ln(n)^p
     1/ n < 1 / ln(n)^p

Ton intuition est bonne. Il faut se rappeler que pour tout $\alpha,\beta>0$ , au voisinage de $+\infty$ , $\ln(x)^\beta$ est négligeable devant $x^\alpha$ (1.), qui lui-même est négligeable devant $e^x$ (2).

C'est un résultat élémentaire de cours dont il faut se rappeler !

Est-ce que tu pourrais le démontrer ? Si non, c'est un bon exercice : démontrer un résultat permet d'avoir de l'assurance vis-à-vis de celui-ci, et on peut par exemple procéder comme suit :

1. Montrer que pour tout $n\in\mathbb{N}$ , on a : $\forall x\in\mathbb{R}_+,\ e^x\geqslant \dfrac{x^n}{n!}$ .
2. En déduire que, pour tout $n\in\mathbb{N},\ \dfrac{e^x}{x^n}\underset{x\to+\infty}{\longrightarrow} +\infty$ .
3.Soit $\beta>0$ . Etablir, pour $x>0$ ,

$\dfrac{e^x}{x^\beta}=\dfrac{e^x}{x^n\cdot x^{\beta-n}}$ ,

avec $n=\lfloor\beta\rfloor$ , la partie entière de $\beta$ , puis en déduire que, pour tout $x>0$ ,

$\dfrac{e^x}{x^\beta}\geqslant \dfrac{e^x}{x^{n+1}}$ .
Indication : La fonction $x\longmapsto x^\beta$ est strictement croissante sur $\mathbb{R}_+^*$ (Pourquoi ?)

4. En déduire (2).

5. Soient $\alpha,\beta>0$ . Etablir, pour $x>0$

$\dfrac{x^\alpha}{\ln(x)^\beta}=\alpha^{\beta} \dfrac{e^{\alpha\ln(x)}}{\left ( \alpha\ln(x)\right )^\beta}$ ,

puis en déduire (1).

Posté par re : convergence 22-08-25 à 11:59

ERRATUM (la fatigue ) :

3.Soit $\beta>0$ . Etablir, pour $x>0$ ,

$\dfrac{e^x}{x^\beta}=\dfrac{e^x}{x^n\cdot x^{\beta-n}}$ ,

avec $n=\lfloor\beta\rfloor$ , la partie entière de $\beta$ , puis en déduire que, pour tout $x>1$ ,

$\dfrac{e^x}{x^\beta}\geqslant \dfrac{e^x}{x^{n+1}}$ .
Indication : Pour $x>1$ fixé, la fonction $\beta\longmapsto x^\beta$ est strictement croissante sur $\mathbb{R}_+^*$ (Pourquoi ?)

Posté par re : convergence 22-08-25 à 17:50

Super merci beaucoup ! je mettrai mes réponses ici quand j'aurais le temps !

Bonne journée

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

analyse en post-bac
24 fiches de mathématiques sur "analyse" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

convergence

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths