Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

Coordonnées ellipsoidiques et model terrestre

Posté par
Aalex00 01-05-19 à 21:40

Bonjour,

On se place dans l'espace euclidien \mathbb{R}^3 usuel.

On considère l'éllipsoide de paramètres  a et  b  (demis-grands axes) définie par :

\begin{cases}x = b \cos{\theta}\cos{\phi} \\ y = a \cos{\theta}\sin{\phi} \\z = b \sin{\theta} \\ \end{cases}           , pour \theta \in [-\pi;\pi] et \phi \in [0;\pi].

L'éllipsoide représente en fait un model approché de la Terre (\theta= longitude ; \phi= latitude).

Et nous nous donnons 2 points de l'éllipsoide : M_1 =\begin{pmatrix}\rho_1 \\ \theta_1 \\ \phi_1\end{pmatrix}et M_2 =\begin{pmatrix}\rho_2 \\ \theta_2 \\ \phi_2\end{pmatrix}. Ces points sont exprimés en coordonnées éllipsoidiques dans un repère dont l'origine O est le centre de notre l'éllipsoide (\rho_i = ||\vect{OM_i}||).

Après calculs trigonométriques, je trouve l'angle \alpha au centre entre M_1 et M_2.

Mais comment calcul-t-on la distance (orthodromique si on en revient au modèle terrestre) exacte M_1M_2 ? Dans le cas sphèrique a=b, il suffirait d'effectuer a \times \alpha...

Posté par
verdurinre : Coordonnées ellipsoidiques et model terrestre 01-05-19 à 22:38

Bonsoir,
ton paramétrage me semble mal adapté.
La terre est à peu près un ellipsoïde de révolution.
L'axe de révolution étant l'axe des pôles.

Il me semblerai judicieux de prendre cet axe dans la base utilisée.
Traditionnellement c'est le troisième axe.

Et on a \begin{cases}x = a \cos{\theta}\cos{\phi} \\ y = a \sin{\theta}\cos{\phi} \\z = b \sin{\phi} \end{cases}

Ce qui me semble plus simple.

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 02-05-19 à 14:20

Bonjour verdurin,

Tout d'abords merci de votre réponse !

Effectivement, j'ai inversé l'axe de révolution ... Une fois cette correction faite, le calcul de l'angle \alpha se simplifie un peu.

Mais ma question persiste toujours pour le calcul de la distance exacte de l'arc M_1M_2 sur l'éllipsoide... En précisant que pour une éllipsoide approximant la Terre, les paramètres a et b étant relativement proche, une moyenne de ces 2 réels multipliée à \alpha donne le résultat avec une erreur correcte de l'ordre de 10^{-4}. Mais dans le cas général, comment procédé avec a >> b ?

Si vous auriez une idée de la façon dont procédé, je suis preneur.

Posté par
verdurinre : Coordonnées ellipsoidiques et model terrestre 02-05-19 à 15:19

Il faut calculer la longueur d'un arc d'ellipse, et ce n'est pas simple.

Tu peux regarder ici la partie circonférence.

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 02-05-19 à 16:58

Effectivement, il est expliqué comment calculer la longueur d'un arc elliptique mais celui ci doit (si j'ai bien compris) être contenu dans un quadrant  de l'ellipse...
Et en regardant les intégrales, je commence à réaliser la complexité des calculs ...

De plus, le calcul de l'équation cartésienne de l'ellipse intersection de l'ellipsoïde avec le plan vectoriel (centre de l'ellipsoïde considéré comme origine) passant par M_1 et M_2 devient vite compliquée dans le cas général..

Enfin bref, merci pour les indications !

Posté par
sylvainc2re : Coordonnées ellipsoidiques et model terrestre 03-05-19 à 01:24


Regarde les formules de Vincenty ici:

Je les avais programmées en langage C il y a un dizaine d'années, elles fonctionnent très bien.  Ce sont des formules numériques qu'il faut itérer jusqu'à ce qu'on obtienne la précision désirée.  

Posté par
sylvainc2re : Coordonnées ellipsoidiques et model terrestre 03-05-19 à 01:29


... et aussi ceci: , plus précisement la section "Navigation on the spheroidal earth", c'est un bon site pour faire des calculs numériques de navigation.

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 03-05-19 à 12:29

Bonjour,

Merci sylvainc2, ces liens sont excellents !

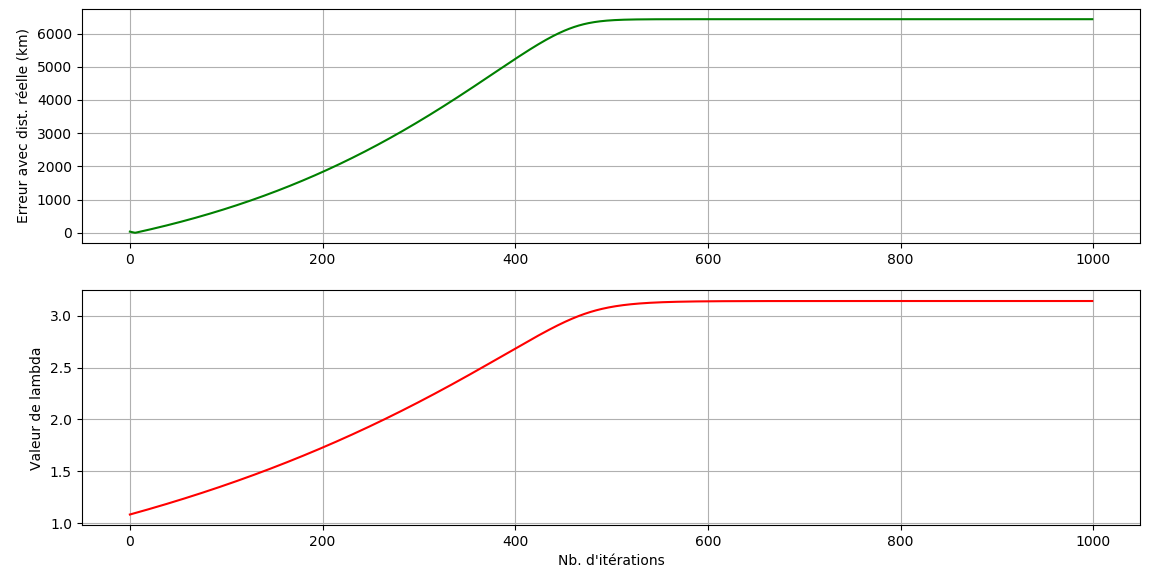
Dans la section {Inverse problem} du lien Wikipedia, j'ai codé les formules puis tracé un graphique de l'erreur faite en fonction du nombre d'itérations. On y voit aussi la convergence de \lambda.
L'erreur tends vers 6400 km en gros ... Mais je ne comprends pas mon erreur ...

Ci-dessous le code (en python, mais si nécéssaire je peux l'expliquer en français parlé) pour calculer une distance orthodromique suivi du graphique évoqué : 


def DISTANCE_ORTHODROMIQUE(Point1, Point2, Model = 'WGS84') :
    # On importe les bon paramètres suivant le modèle choisi.
    [a, b, f] = PARAMETRES_MODEL_ELLIPSOIDE_TERRE(Model)
    # On convertit en mètres (comme sur Wikipedia).
    a = 1000 * a
    b = 1000 * b
    # On importe les coordonnées Longitude / Latitude en radian de 2 points.
    [Long1, Lat1] = CONVERT_COORDONNEES_DEGRES_TO_RADIANS(Point1)
    [Long2, Lat2] = CONVERT_COORDONNEES_DEGRES_TO_RADIANS(Point2)

    # Chaque variable calculée porte le même nom que sur Wikipedia pour rester clair.
    U1 = math.atan((1 - f) * math.tan(Lat1))
    U2 = math.atan((1 - f) * math.tan(Lat2))
    L = Long1 - Long2

    # Nombre d'itérations qu'on effectuera : 1000
    for iter in range(0, 1000) :
        sin_sigma = math.sqrt(pow(math.cos(U2)*math.sin(L), 2)+pow(math.cos(U1)*math.sin(U2) \
                    -math.sin(U1)*math.cos(U2)*math.cos(L), 2))
        cos_sigma = math.sin(U1)*math.sin(U2) + math.cos(U1)*math.cos(U2)*math.cos(L)
        sigma = math.atan2(sin_sigma, cos_sigma)


        sin_alpha = (math.cos(U1)*math.cos(U2)*math.sin(L))/sin_sigma
        cos_2sigma_m = cos_sigma - (2*math.sin(U1)*math.sin(U2))/(1-pow(sin_alpha, 2))
        C = (f/16)*(1-pow(sin_alpha, 2))*(4 + f*(4 - 3*(1-pow(sin_alpha, 2))))


        lamb = L + (1-C)*f*sin_alpha*(sigma + C*sin_sigma*(cos_2sigma_m + C*cos_sigma*(-1+2*pow(cos_2sigma_m, 2))))
        L = lamb


    u_carre = (1-pow(sin_alpha, 2))*((a*a-b*b)/(b*b))
    A = 1 + (u_carre/16384)*(4096 + u_carre*(-768 + u_carre*(320 - 175*u_carre)))
    B = (u_carre/1024)*(256 + u_carre*(-128 + u_carre*(74 - 47*u_carre)))

    Delta_sigma = B * sin_sigma * (cos_2sigma_m + 0.25*B * (cos_sigma * (-1 + 2*pow(cos_2sigma_m, 2)) \
                 - B/6 * cos_2sigma_m * (-3 + 4*pow(sin_sigma, 2)) * (-3 + 4*pow(cos_2sigma_m, 2))))
    s = b*A*(sigma - Delta_sigma)
    return s


Coordonnées ellipsoidiques et model terrestre

Posté par
sylvainc2re : Coordonnées ellipsoidiques et model terrestre 04-05-19 à 03:14

La variable "L" ne doit pas changer à l'intérieur de la boucle, c'est la variable que tu nommes "lamb" qui change.  Regarde bien dans la page wiki, il y a une distinction entre L et \lambda.

Aussi tu ne devrais pas coder le nombre d'itérations avec un "for", tu devrais faire comme ceci:
while True:
   ...
   avant la ligne lamb = L + ...etc... tu mets:
    D = lamb
   puis pour fermer la boucle:
        if (not(math.fabs(lamb-D)>EPSILON)):
            break


où EPSILON est une constante que tu définis du genre EPSILON = 0.0000000001

Ca devrait fonctionner maintenant.

Posté par
sylvainc2re : Coordonnées ellipsoidiques et model terrestre 04-05-19 à 03:22

Et puis pour être clair à l'intérieur de la boucle c'est la variable \lambda soit "lamb" qui doit être utilisée dans les sin et cos, pas L sauf à la ligne
     lamb = L + (1-C)*f ... etc...
Là c'est bien L, qui ne doit pas changer je le répète.

Donc tu dois initialiser lamb = L avant d'entrer dans la boucle pour que ca fonctionne correctement.

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 04-05-19 à 15:29

Bonjour,

Merci pour les corrections. J'ai modifié le code en conséquence : 

def DISTANCE_ORTHODROMIQUE_3(Point1, Point2, Model = 'WGS84') :
    # On importe les bon paramètres suivant le modèle choisi.
    [a, b, f] = PARAMETRES_MODEL_ELLIPSOIDE_TERRE(Model)
    # On convertit en mètres (comme sur Wikipedia).
    a = 1000 * a
    b = 1000 * b
    # On importe les coordonnées Longitude / Latitude en radian de 2 points.
    [Long1, Lat1] = CONVERT_COORDONNEES_DEGRES_TO_RADIANS(Point1)
    [Long2, Lat2] = CONVERT_COORDONNEES_DEGRES_TO_RADIANS(Point2)

    # Chaque variable calculée porte le même nom que sur Wikipedia pour rester clair.
    U1 = math.atan((1 - f) * math.tan(Lat1))
    U2 = math.atan((1 - f) * math.tan(Lat2))
    L = Long1 - Long2
    tolerance = 0.000000000001

    lamb = L
    while True :
        D = lamb

        sin_sigma = math.sqrt(pow(math.cos(U2)*math.sin(lamb), 2)+pow(math.cos(U1)* \
                    math.sin(U2)-math.sin(U1)*math.cos(U2)*math.cos(lamb), 2))
        cos_sigma = math.sin(U1)*math.sin(U2) + math.cos(U1)*math.cos(U2)*math.cos(lamb)
        sigma = math.atan2(sin_sigma, cos_sigma)

        sin_alpha = (math.cos(U1)*math.cos(U2)*math.sin(lamb))/sin_sigma
        cos_2sigma_m = cos_sigma - (2*math.sin(U1)*math.sin(U2))/(1-pow(sin_alpha, 2))
        C = (f/16)*(1-pow(sin_alpha, 2))*(4 + f*(4 - 3*(1-pow(sin_alpha, 2))))

        lamb = L + (1-C)*f*sin_alpha*(sigma + C*sin_sigma*(cos_2sigma_m + C*cos_sigma* \
               (-1+2*pow(cos_2sigma_m, 2))))

        if abs(lamb - D) < tolerance :
            break

    u_carre = (1-pow(sin_alpha, 2))*((a*a-b*b)/(b*b))
    A = 1 + (u_carre/16384)*(4096 + u_carre*(-768 + u_carre*(320 - 175*u_carre)))
    B = (u_carre/1024)*(256 + u_carre*(-128 + u_carre*(74 - 47*u_carre)))

    Delta_sigma = B * sin_sigma * (cos_2sigma_m + 0.25*B * (cos_sigma * (-1 \
                  + 2*pow(cos_2sigma_m, 2)) - B/6 * cos_2sigma_m * (-3 + 4*pow(sin_sigma, 2)) \
                  * (-3 + 4*pow(cos_2sigma_m, 2))))
    s = b*A*(sigma - Delta_sigma)
    return s/1000


En revanche, après une batterie de tests cette méthode présente une moyenne d'erreur de l'ordre de 0.1% et ne fonctionne pas sur l'équateur (division par 0 en rouge), ni pour des points antipodaux (mais une alternative est possible : ).

Ce qui me gène, c'est qu'avec la technique sur mes 2 premiers posts, les erreurs sont déjà de l'ordre de 0.01% ... et le nombres d'opérations bien moindre ...

Peut-être qu'une erreur persiste dans mon code pour améliorer la précision ?

Posté par
sylvainc2re : Coordonnées ellipsoidiques et model terrestre 04-05-19 à 23:29

Je comprends pas, quand tu parles d'erreur, c'est par rapport à quoi? Parce que j'ai ressorti mon vieux code en langage C et je l'ai comparé avec le tien en python avec quelques jeux de test et les deux me donnent le même résultat au mm près pour la distance.  D'après moi, ton programme est correct.  

Aussi il existe des packages en python déjà faits, par exemple geopy et une autre référence donnée en bas de page ici: https://movable-type.co.uk/scripts/latlong-vincenty.html

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 05-05-19 à 10:53

Bonjour,

Par exemple on se donne les coordonnées : 

    Point1 = [138.363531, 84.946308]
    Point2 = [-22.095115, 70.148730]

écrites sous la forme [Longitude , Latitude].

En appliquant la fonction  du post 04-05-19 à 15:29, on obtient : 

>>> print(DISTANCE_ORTHODROMIQUE_3(Point1, Point2), "km - Modèle WGS84")
2754.54660537193 km - Modèle WGS-84

Or en utilisant l'outil mesurer une distance sur Google Map ou encore en allant sur , on trouve :
2743.122 km
Je pense que ces outils sont fiables ou pas trop ...


Effectivement, je pense pas qu'il y est d'erreur dans le code de la fonction DISTANCE_ORTHODROMIQUE_3 puisque en allant sur le lien que tu me proposes , on peut y calculer en ligne une distance par les méthodes de Vincenty et voila :

Coordonnées ellipsoidiques et model terrestre

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 05-05-19 à 11:27

Je viens de reprendre la fonction .distance.vincenty du module geopy évoqué : 

def measure(Point1, Point2):
        [lng1, lat1] = CONVERT_COORDONNEES_DEGRES_TO_RADIANS(Point1)
        [lng2, lat2] = CONVERT_COORDONNEES_DEGRES_TO_RADIANS(Point2)
        [major, minor, f] = PARAMETRES_MODEL_ELLIPSOIDE_TERRE('WGS-84')

        delta_lng = lng2 - lng1

        reduced_lat1 = math.atan((1 - f) * math.tan(lat1))
        reduced_lat2 = math.atan((1 - f) * math.tan(lat2))

        sin_reduced1, cos_reduced1 = math.sin(reduced_lat1), math.cos(reduced_lat1)
        sin_reduced2, cos_reduced2 = math.sin(reduced_lat2), math.cos(reduced_lat2)

        lambda_lng = delta_lng
        lambda_prime = 2 * pi

        iter_limit = 100 # Je crois que dans l'original c'était 20 ...

        i = 0

        while (i == 0 or (abs(lambda_lng - lambda_prime) > 10e-12 and i <= iter_limit)):
            i += 1

            sin_lambda_lng, cos_lambda_lng = math.sin(lambda_lng), math.cos(lambda_lng)

            sin_sigma = math.sqrt( (cos_reduced2 * sin_lambda_lng) ** 2 + \
                        (cos_reduced1 * sin_reduced2 - sin_reduced1 * cos_reduced2 * cos_lambda_lng) ** 2 )

            if sin_sigma == 0:
                return 0  # Coincident points

            cos_sigma = ( sin_reduced1 * sin_reduced2 + cos_reduced1 * cos_reduced2 * cos_lambda_lng )

            sigma = math.atan2(sin_sigma, cos_sigma)

            sin_alpha = ( cos_reduced1 * cos_reduced2 * sin_lambda_lng / sin_sigma )
            cos_sq_alpha = 1 - sin_alpha ** 2

            if cos_sq_alpha != 0:
                cos2_sigma_m = cos_sigma - 2 * ( sin_reduced1 * sin_reduced2 / cos_sq_alpha )
            else:
                cos2_sigma_m = 0.0  # Equatorial line

            C = f / 16. * cos_sq_alpha * (4 + f * (4 - 3 * cos_sq_alpha))

            lambda_prime = lambda_lng
            lambda_lng = ( delta_lng + (1 - C) * f * sin_alpha * ( sigma + C * sin_sigma * ( cos2_sigma_m + C \
                         * cos_sigma * ( -1 + 2 * cos2_sigma_m ** 2 ) ) ) )

        if i > iter_limit:
            raise ValueError("Vincenty formula failed to converge!")

        u_sq = cos_sq_alpha * (major ** 2 - minor ** 2) / minor ** 2

        A = 1 + u_sq / 16384. * ( 4096 + u_sq * (-768 + u_sq * (320 - 175 * u_sq)) )

        B = u_sq / 1024. * (256 + u_sq * (-128 + u_sq * (74 - 47 * u_sq)))

        delta_sigma = ( B * sin_sigma * ( cos2_sigma_m + B / 4. * ( cos_sigma * ( -1 + 2 * cos2_sigma_m ** 2 \
                      ) - B / 6. * cos2_sigma_m * ( -3 + 4 * sin_sigma ** 2 ) * ( -3 + 4 * cos2_sigma_m ** 2 ) ) ) )

        s = minor * A * (sigma - delta_sigma)
        return s


Je l'ai ensuite testé avec les points de mon post précédent, et je trouve la même chose donc cela confirme que les codes sont corrects : 

>>> print(GPS.DISTANCE_ORTHODROMIQUE_3(A[3], B[3]), "km.")
    print(GPS.measure(A[6], B[6]), "km - Fonction reprise de geopy.")
2754.54660537193 km.
2754.5466053719297 km - Fonction reprise de geopy.


Mais dans ce cas, d'où une telle différence peut-elle venir ? Peut être que ces méthodes convergent autant qu'on le souhaite mais vers une approximation qui elle conserve une certaine erreur ...

Posté par
sylvainc2re : Coordonnées ellipsoidiques et model terrestre 05-05-19 à 20:45

Google maps semble calculer la distance sur grand cercle, avec un rayon terrestre de 6371km qui est la valeur moyenne acceptée du rayon.  Avec ton exemple ci-haut j'obtiens aussi 2743122.395855m sur grand cercle.  Donc il ne faut pas comparer la formule de Vincenty avec google maps, c'est pas le même calcul.

Remarque qu'il y a une version de Vincenty qui tient compte de l'altitude des points au-dessus ou sous l'ellipsoide de référence, je pensais que c'était ca que google maps calculait, mais non finalement.

Posté par
Aalex00re : Coordonnées ellipsoidiques et model terrestre 05-05-19 à 21:59

Effectivement tu as raison. Je suis tout même surpris que Google Map se contente d'une telle approximation ... Enfin, on peut leur pardonner puisque la version Globe vient récemment de remplacer la version Mercator ...

Enfin bref, merci pour tout le temps que tu as pu consacrer à cette conversation.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !