Bonjour,
poste nous ton croquis

Bonjour à tous
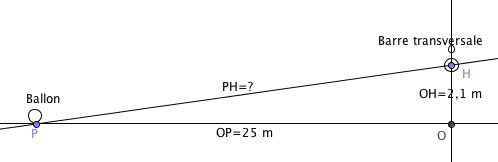
J'ai fait un petit dessin
On ne sait pas précisément où la pointe du pied du tireur va percuter le ballon posé au sol. J'ai fait comme si le point P était au sol
Si le ballon doit passer à 20 cm sous la barre transversale, le centre H de ce dernier sera à 2,44-0,20-0,14=2,1 m du sol, soit OH=2,1 m
Et PH²=OP²+OH²d'où PH= ?
l'affirmation de Platini est vraie car si PH=PH+20 cm et OP=25 m
le calcul montre que le ballon passera au-dessus de la barre transversale et le gardien ne pourra pas le toucher

Bonjour,

c'est ça ou pas ça ...

de toute façon le but (!) de Platini n'est certainement pas de passer au dessus de la barre !

"le ballon se loge dans la lucarne sans que le gardien puisse l'arrêter"
(bof, ça dépendra peut être bien du gardien, dont on ne sait rien dans cet énoncé, s'il l'arrête ou pas)

Bonjour mathafou
En effet on peut supposer que Michel Platini mettrait la balle dans la cage, cependant si on s'en tient à l'énoncé qui dit " si la distance HP fait 20 cm de plus que la distance OP" et "application : le coup franc se situe à 25 m"
alors HP=25,2 m
et OH²=HP²-OP²=25,2²-25²=635,04-625=10,4
et OH=10,4=3,16 m !
ou il y a une erreur d'énoncé ou alors je n'y comprends rien

normal tant qu'on n'aura pas le vrai énoncé (la définition de tous les points et la figure) ce ne sera que de la "discussion de salon"

l'énoncé (le bout que j'ai déja cité) dit explicitement que pour la nouvelle valeur le ballon rentre et Platini marque le but (c'est son objectif)

Bonjour à tous,

Tout d'abord permettez moi de vous remercier pour votre aide. Je ne connaissais pas ce forum, mais maintenant  j'apprécie ses intervenants.

Pour en revenir  au sujet qui nous préoccupe je peux donner une indication supplémentaire: il s'agit d'un exercice dans le cadre de la réciprocité du théorème de Pythagore .
J'ai bien relu l'énoncé il n'y a pas d'erreur de transcription.

Pour le moment je ne peux pas vous envoyer de schéma car le volume du fichier est trop volumineux. Il s'agit d'une reproduction d'une photo .Je vais essayer de résoudre le problème . Merci de votre compréhension .

Bonne journée à tous

JP

lire attentivement comment redimensionner une image...en la mettant en jpg, j'en connais pas qui ne passe pas !

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

Bonsoir à tous

Comme promis voici la photo concernant l'exercice.
J'espère que cela vous sera utile.
Encore merci pour votre aide.  
JP

bof
c'est pas la photo de la page du livre qu'on attendait !
mais une photo de la figure
de la figure seule
ce qui permet de la mettre bien plus grande et bien moins floue !!
(on ne voit même pas les noms des points !!! donc inutilisable, les visages des joueurs on s'en fiche, les noms des points pas du tout)

le texte doit être recopié (au clavier, en entier, mot à mot)
"on va dire" que c'est le texte déja donné, en l'absence de possibilité de lire le texte de toute façon INTERDIT sur la photo.
mais il me semble qu'il y a plus de texte sur cette photo que ce qui a été copié ici.

et le grand blanc plein de taches en dessous est totalement inutile.

donc on en est exactement au même point = les calculs de mijo qui sont en contradiction avec ce qui est demandé (dans la lucarne)
et on ne sait toujours pas en vrai ce qu'il faut calculer.

Bonjour à tous,

D'accord, excusez moi je suis confus, je pensais sincèrement bien faire . Je vais essayer de mieux faire .

Bonne journée
JP

Bonjour à tous,

Je vous ai mis le document original   tel  qu'il a été fourni  dans l' énoncé du devoir. (il s'agit d'un DM maison demandé par un professeur de collège  )
Le triangle a été matérialisé sur la photo par un "croquis" (visible sur la photo) avec le point H centre du ballon au sommet du triangle,  le point O à la gauche du triangle près du poteau de but mais légèrement en avant de la ligne de but   et le point P sur le pied droit du joueur.
J' espère que cela vous permettra de mieux appréhender la question posée.

Deux précisions :
A la relecture de l'énoncé je me suis rendu compte  d'une omission sur la première donnée
Je vous remets l'énoncé mot à mot par rapport à l'original.

- la cage de foot mesure 2,44 m  EN HAUTEUR
- le ballon a un rayon de 14 cm (diamètre 28 cm)
- la balle doit passer à 20 cm sous la barre transversale
- le triangle OHP est rectangle en O
- le point H est au centre du ballon, le point P est le pied du joueur
- Michel Platini a calculé que si la distance HP fait 20 cm de plus que la distance OP alors le ballon se loge dans la lucarne sans que le gardien puisse l'arrêter
Application : le coup franc se situe à 25 m

Calculer la distance PH pour que le ballon atteigne son but. Justifie et rédige.




Secundo par rapport à la remarque faite "il me semble qu'il y a plus de texte sur cette photo que ce qui a été copié ici"

c'est vrai voici le texte en plus situé sur le haut de la photo :

1) Les sportifs ont de plus en plus recours aux mathématiques pour améliorer leurs performances. le 1er footballeur qui en a eu l'idée est Michel Platini (en 1980) avec ses fameux coups francs directs.


***image recadrée***

Bonjour
Je reviens vers vous pour vous dire que je vous remercie pour votre aide
bonne journée à tous
JP

c'est mieux, on arrive à lire.
mais tu es vraiment fâché avec le traitement correct des images
à quoi sert le grand vide tout autour de la figure ? à rien ! à part alourdir inutilement l'image
il faut rogner pour supprimer ce grand vide inutile
et ce avant de redimensionner, après c'est trop tard. le mal est fait (perte de définition etc)
bon passons. pour la prochaine fois tu apprendras à réellement utiliser Paint


cet énoncé est encore plus loufoque que ce que donne les calculs de mijo :

Application : le coup franc se situe à 25 m : OP = 25m

Michel Platini a calculé que si la distance HP fait 20 cm de plus que la distance OP

Calculer la distance PH

bein PH et HP c'est pareil
donc PH = OP + 20 cm, c'est Platini qui le dit

donc PH = 25,2 m
terminé.
tout calcul supplémentaire serait une autre question que celle écrite dans l'énoncé.

pour calculer OH qui n'est pas demandé c'est Pythagore
et avec PH = 25,2 et OP = 25 ça donne OH ≈ 3,17 m bien au dessus de la barre qui est à 2,44 m
et donc le ballon n'atteint pas son but
Platini c'est gouré et son prétendu usage des maths dans le football est du pipeau pour les médias et se faire mousser.

on peut faire les calculs à l'envers avec la même conclusion
on impose OH = 2.44 - 0.2 = 2.24 (pour que le ballon entre dans le but) voir pire 2.44 - 0.2 - 0.14 = 2.10 si c'est le haut du ballon qui doit passer à 20 cm au dessous de la barre

et calculer ce que aurait du être "la règle de Platini" en calculant PH nous même (et pas selon Platini)

ça fait (Pythagore encore) PH ≈ 25.10 (ou 25.09)
la règle de Platini aurait donc dû être : PH = 10cm de plus que OP (ou 9 cm de plus)
la conclusion est la même : Platini fait de l'esbroufe et en vrai c'est son habileté sans aucun calcul qui fait le boulot.

Je constate que la résolution de ce problème est à priori trouvée.  
Un grand MERCI  à toute l'équipe !!

Bonne journée à vous tous
JP

PS : Je vais tâcher de faire mieux avec Paint la prochaine fois . Encore merci pour votre disponibilité et vos conseils .

"la résolution de ce problème est à priori trouvée."
hum

des calculs possibles à partir d'un tel énoncé.

et je n'ai donné que les résultats, en valeurs approchées, les calculs réels (Pythagore) c'est à toi de les faire (de les rédiger)