Inscription / Connexion Nouveau Sujet
courbe fonctions exponentielles et tangente
bonjour,
j'ai cet exo :
C est la courbe représentative d'une fonction f définie sur R par f(x) = (ax+b)ex T est la tangente à C au point A(0;1) de C
a) trouver a et b
b) calculer les coordonnées du point B de C ayant une tangente parallèle a l'axe des abscisses et placer B
Alors voila ce que j'ai fait... Pouvez vous me dire si j'ai bon ? Ensuite, je n'ai pas trouvé b car je ne sais pas si je dois le faire grace a un calcul ( si oui lequel ? ) ou avec ma courbe et ma tangente de l'exo ... ( comment? )
f(0) = b * e0 =1
donc b=1
J'ai calculé la dérivée, est ce utile? Est elle bonne?
F'(x) = aex + (ax+b )ex
Merci de votre aide
Tu as trouvé le bon b et ta dérivée est exacte
après j'ai trouvé a = -1, car avec l'équationd e la tangente ça te donne , ax+x+1=1 d'où ax+x=0 et enfin ax=-x donc x=-a ! un peu hazardeu mais ça doit être un truc comme ça !
donc f(x)= (-x+1)ex
F'(x) = - ex+ (-x+1)ex
Ensuite pour la question b) , il faut que tu calcule l'équation de la tangente de la courbe C avec y= F'(a) (x-a) + f(a)
Tangente paralléle à l'axe des abscisses = tangente horizontale , c'est-à-dire avec un coeff directeur = 0 .
L'équation de la tangente au point a est de la forme , y= f'(a) (x-a) + f(a)= ( - ea + (-a+1)ea ) (x-a)+f(a)
On développe, y = -a ea (x-a)+f(a)
Le coefficient directeur de ta tangente c'est donc tout ce qu'il y a avant ton x doit être égal à 0 ,
c'est-à-dire -a ea = 0
Or on a , ea strictement sup à 0 donc , a = 0
la courbe C admet une tangente horizontale au point a= 0 , tu remplace dans ton équation de y = -a ea (x-a)+f(a) ( à finir de dév.) et tu dois arriver à y=1 .
B (0,1) . avec la calculette graphique ça donne un beau truc !
Bon je me suis un peu éparpillé mais les idées sont là, à toi de les mettre à ta sauce !
Bon courage.
bonjour corsilili
tu dis "après j'ai trouvé a = -1, car avec l'équation de la tangente ça te donne , ax+x+1=1 d'où ax+x=0 et enfin ax=-x donc x=-a ! un peu hazardeu mais ça doit être un truc comme ça !"
==> déjà, quelle équation de la tangente ?
==> ensuite tu déduis de ax=-x que x=-a 
Avec les données de l'énoncé, il y a une famille de courbe Ca : y=(ax+1)ex
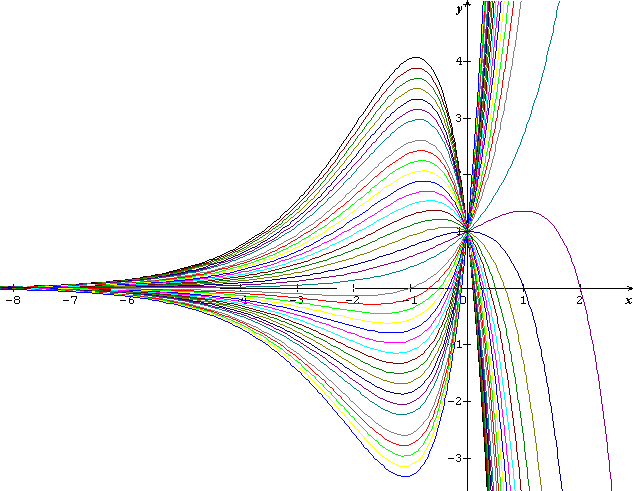
Que tchomais nous précise T...
Rudy
mais , avec l'énoncé fourni, d'où tires-tu la relation "ax+x+1=1" ?
éventuellement "ax+1+a=1" je comprendrais une pente égale à 1...
Rudy
lol je vois que ca cogite beaucoup pour moi je vois. J'ai demandé a mon prof si on avait le droit d'utiliser le graphique pour trouver a... Et oui effectivement. J'ai donc trouver mon coef directeur et grace a la dérivée.
En gros je trouve a = 2 ( si ca vous interesse)


