Bonjour,

c'est assez amusant merci .
Bien sûr les clous ont un diamètre nul.
On cherche.....

Suite
à priori

 Cliquez pour afficher

Si L=2    A=
Si L=3    A = 22

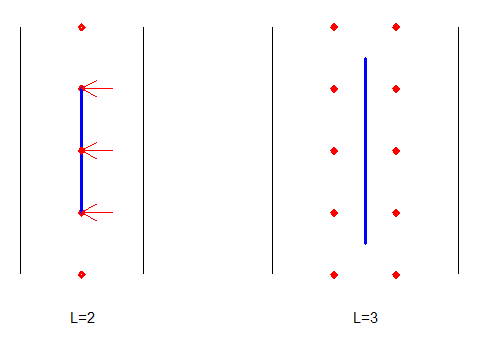
Oui , les clous n'ont pas d'épaisseur et on suppose la bande de longueur infinie . Il me semble que pour L=2 on peut retourner une aiguille de longueur 2

Imod

Pour ça passe et c'est le maximum absolu
Imod

Suite,

 Cliquez pour afficher

Pour L=2 je pense que la contrainte oblique est 5 >2,
donc 2  est le maximum.
Pour L=4  la contrainte oblique est  10<4 donc valable

Oui , ça passe pour mais est-ce le maximum ? Il y a un nombre imposant de "contraintes obliques" qui gonfle rapidement avec la largeur de la bande . Il me semble que pour L=1 ; 2 ; 3 on a la réponse , pour quatre il faudrait justifier un minimum

Sur une surface illimitée de clous , on retourne n'importe quelle aiguille sans problème mais ici il y a des effets de bande qui compliquent énormément la chose .

La résolution pour les premières valeurs me satisferait complètement mais si on va plus loin :  je n'ai rien contre

Imod

Pour L = 4, j'arrive à faire passer une aiguille de en 5 mouvements.

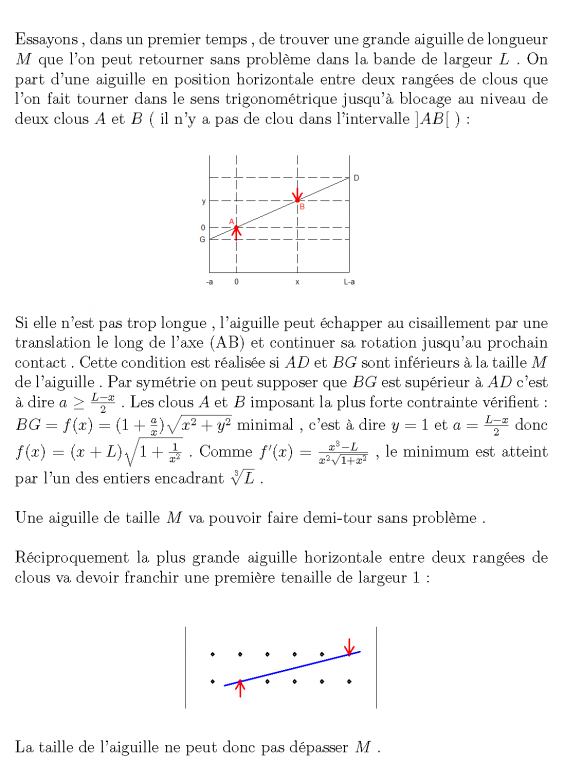
En règle générale, je pense bien que la contrainte la plus forte est le passage du dernier clou juste avant l'horizontale. Ce qui donne pour :  

Je suis plutôt d'accord avec ta formule LittleFox mais il est difficile d'argumenter sur le pire passage tant qu'on a pas établi un minimum de stratégie ( sans chercher forcément à limiter les mouvements ) . J'avais pensé réduire les mouvements à des rotations autour de l'extrémité de l'aiguille  située sur un bord de la bande ou à des translations dans la direction de l'aiguille amenant une de ses extrémités sur le bord de la bande . On peut ( par exemple ) partir d'une aiguille en position horizontale accrochée au bord gauche de la bande et décrire les mouvements et les pentes rencontrés .  

Imod

PS : je rappelle que je n'ai pas de réponse au problème

Désolé je pense à voix haute

L'idée précédente n'est pas la bonne , mais on peut envisager de tourner autour du dernier clou avant le bord avant de faire glisser l'aiguille vers l'autre bord en laissant juste un peu de place pour le mouvement suivant

Il n'est pas simple ce problème , j'espère qu'il vous intrigue autant que moi ::

Imod

Pour L=6 , je n'arrive pas à retourner l'aiguille avec la valeur fournie par LittleFox , la pente 1/2 semble infranchissable en partant d'une aiguille horizontale reposant sur un tapis de clous .

Imod

Dernier message solo ( je ne vais pas monologuer éternellement ) .

Sauf erreur , déjà pour L=5 l'aiguille de longueur ne passe pas la pente p=1 . On a trouvé la taille maximale de l'aiguille pour 1<L<5 , je ne pense pas qu'on puisse établir une formule générale sans se salir un peu les mains avec d'autres valeurs de L .

Le problème est sans doute peu intéressant ou trop difficile

En tout cas un grand merci à Dpi et LittleFox pour la participation

Bien sûr je vous tiens au courant si je trouve un peu mieux que de vagues suppositions .

Imod

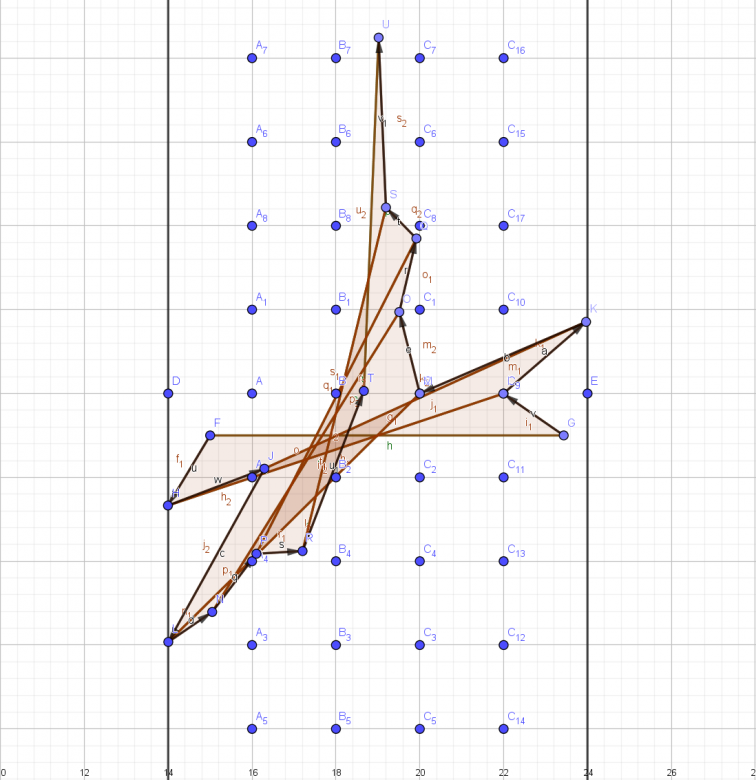
Pour L=5, voici une possibilité pour passer une aiguille de longueur .

Ça passe tout juste p=1 mais et donc ça passe.

C'est pas que le problème est peu intéressant mais frustrant car difficile de vérifier sa réponse. Car il y a plein de chemins possibles, pleins de contraintes possibles et que tout ça est vite fouillis et difficile à représenter.

Je n'ai pas encore de chemin avec L=6, mais je ne suis pas sûr d'avoir tord non plus

Merci pour ta réponse LittleFox

Pour L=5 , j'avais fait le dessin à la main , le blocage pour p=1 semblait limite donc douteux , je ne serais donc pas étonné que ça passe .

Les passages possibles de l'aiguille ne sont pas vraiment nombreux , les cas intéressants sont ceux où l'aiguille est en contact avec au moins deux clous et alors les pentes sont en nombre fini .

Je n'ai pas le temps d'illustrer ce soir mais il me semble que pour une aiguille donnée on obtient les meilleurs déplacements de la façon suivante :

- On cale l'aiguille à gauche posée sur une ligne horizontale de clous .

- On fait glisser l'extrémité gauche de l'aiguille vers le bas en suivant le bord et on s'arrête lorsque l'aiguille touche un nouveau clou .

- On fait glisser l'aiguille le long des points de contact jusqu'au bord droit de la bande .

- On fait glisser l'extrémité droit de l'aiguille vers le haut jusqu'à un nouveau blocage  ...

Bien sûr c'est la taille de l'aiguille qui va déterminer le point de blocage donc la trajectoire de l'aiguille mais pour une taille donnée le mouvement est parfaitement défini . On peut d'ailleurs décrire parfaitement le mouvement sans illustration en donnant simplement la succession des pentes amenant à la verticale ( La suite est symétrique ) .

Même si je n'ai aucune preuve j'ai du mal à croire que l'on puisse faire mieux avec des passages avec glissement par des pentes intermédiaires ou des retours .

Imod






  

J'ai regardé en détail l'illustration de LittleFox pour L=5 , en effet ça passe et du coup rien ne va plus

La borne supérieure n'est pas la bonne et il faut accepter de tourner autour d'un point qui n'est pas un clou . Si on accepte tout déplacement on rentre vite dans un "no mans lands" sans loi et donc sans résultat possible .  On peut sans doute limiter les déplacements à des translations dans le sens de l'aiguille ou perpendiculaires à cette direction et à des rotations autour d'un point de l'axe de la bande ( à coordonnées rationnelles ) .

Il y a beaucoup de grain à moudre et il va falloir de très bons meuniers

Si on s'intéresse au problème il faut vraiment passer au crible les bandes 4 ,5 et 6 et suivantes pour trouver un fil d'Ariane .

Je vais regarder si je peux ramener les déplacements de LittleFox à des déplacements élémentaires .

Bon courage à ceux qui essaient encore , personnellement , je commence à peiner un peu grave

Imod

Bonjour,

C'est le seul exercice actuel ( celui de luzak  est trop complexe).
Il mériterait donc l'attention des habitués.
Comme les paramètres sont bien posés ,il doit y avoir une loi dont on sait déjà
que 2 est le minimum est L le maximum ensuite on ne voit que du Pythagore ...

Quelque chose comme

Pour te rassurer Imod, il est tout à fait possible de décomposer les mouvements que je fais pour L=5 en rotations autour d'un clou à coordonnées entières et translations selon l'axe de l'aiguille. C'est juste moins clair sur le dessin et m'a mené à des erreurs du genre le clou de rotation passe subitement de gauche à droite de l'aiguille ou inversement.

Pour L=6, il semblerait que ma solution soit trop optimiste. Je n'arrive pas non plus à passer la pente 1/2.

Quelques pistes pour la recherche et peut-être une recherche systématique automatisée :

- Une aiguille verticale peut toujours être déplacée dans n'importe quelle "colonne" entre les clous. En effet, on peut aller aussi loin que l'on veut en haut ou en bas et donc une pente infinitésimale suffit à faire passer l'aiguille d'une colonne à l'autre.

- Il suffit donc d'avoir une séquence de mouvement qui rend une aiguille de l'horizontale à la verticale pour avoir une solution.

- A chaque étape (sauf la dernière verticale) on a un ensemble de clous à gauche de l'aiguille et un autre à droite. Cette séparation peut être résumée à connaitre 4 clous 2  de chaque côté. Aucun des autres clous ne pouvant passer de l'autre côté sans faire passer l'un de ses 4 clous.

- Toute séquence de mouvements peut être représentée comme une séquence de ces 4 clous (potentiellement longue) où à chaque mouvement un des 4 clous passe de l'autre côté.

- Les clous de départs peuvent être (1,0), (L-1,0), (1,1) et (L-1,1). Les bords gauche et droit sont x = 0 et x = L.

- On est à la verticale dès que le clou à gauche avec l'abscisse la plus grande a une abscisse plus petite que le clou à droite avec l'abscisse la plus petite.

- Toute position des 4 clous peut être déplacée verticalement de façon à ce que l'ordonnée minimale soit 0. La solution obtenue à partir de cette position est équivalente. (Permet de diminuer l'espace de recherche).

- Pour passer le clou en haut à droite , le clou à gauche en bas étant (x_{bg},y_{bg}), l'aiguille doit être plus petite que . Les autres passages sont symétriques.

- Le passage d'un des 4 clous change les 3 autres de façon non triviale mais calculable (il me reste à faire le calcul ).

- Ensuite il reste "juste" à trouver la séquence qui arrive à la verticale avec la plus grande longueur pour l'aiguille. (Comment éviter les séquences infinies ).

Voilà, reste plus qu'à résoudre et programmer

Je suis complètement d'accord avec tes remarques et en effet le côté de l'aiguille en contact avec les clous est essentiel . Je m'étais dit qu'on ne changeait rien en laissant glisser l'aiguille sur l'autre bord en suivant deux clous et qu'on libérait simplement l'aiguille de certains contacts . En fait si l'espace de translation est suffisant on peut aussi inverser certains contacts , ce qui change pas mal de choses .



Je ne connais rien à la programmation mais  il me semble que si on veut essayer de résoudre le problème par cette voix on peut se limiter aux pentes rationnelles croissantes dont le numérateur et le dénominateur sont inférieurs à L , on limite ainsi le nombre de déplacements ( attention tout de même aux glissements pour changer le sens des contacts ) .

D'autre part je doute qu'on puisse régler l'ensemble du problème sans avoir au moins résolu à la main ou autrement les cas L=5 et L=6

Content de toute façon de voir que certains ne lâchent pas le problème  

Imod

  

Il me semble que la pente de l'aiguille n'est pas suffisante pour caractériser une position de l'aiguille.

Pour moi, un ensemble de positions équivalentes de l'aiguille est l'ensemble des positions que peut prendre l'aiguille par translation selon l'axe de celle-ci, translation verticale d'un nombre entier d'unités et rotation sans que l'axe de l'aiguille ne croise un clou.

Je représentait cet ensemble de positions par les 4 clous qui limitent ces positions (le plus bas des clous ayant comme ordonnée 0). Mais je me rend compte qu'on peut encore simplifier avec les coordonnées de seulement 2 clous, l'un à gauche, d'ordonnée 0 et en dessous de l'ensemble des aiguilles et l'autre à droite et au dessus de l'ensemble des aiguilles. De plus la différence d'abscisse et la différence d'ordonnée doivent être premières entre elles.

Il reste donc 3 coordonnées entières, 3 degré de liberté ce qui correspond à une droite (de pente rationnelle dont le dénominateur est inférieur à L, pas nécessairement le numérateur).

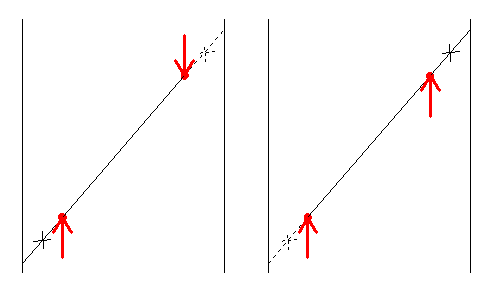
Il est toujours possible d'inverser le cas où le point au dessus serait à gauche du point en dessous en "poussant" sur la droite passant par l'aiguille dans le sens trigonométrique jusqu'à être bloqué sur les deux nouveaux clous.

Le passage d'un état à l'autre est une rotation autour de l'un des deux points rotation qui peut avoir deux sens. Donc 4 états possibles. Ils ne sont plus très difficile à calculer. Un exemple de rotations autour du point gauche-dessous :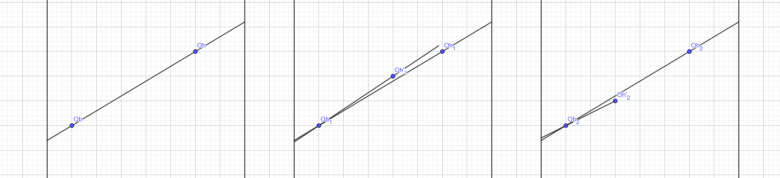

Je ne suis plus très loin d'une implémentation. Imod est-ce que tu peux me confirmer que cette représentation est "valide" dans le sens où chaque position d'aiguille a une et une seule représentation ?

Il semble tout de même que la pente est quasi-suffisante pour caractériser la position à condition de manœuvrer systématiquement l'aiguille le long de sa direction pour faire passer un maximum de clous du "bon" côté . Il faudra bien sûr repérer le nouveau pivot après chaque rotation+ glissements . On peut restreindre aisément l'étude à un passage de l'horizontale avec tous les clous en dessous à la verticale . Les pentes qu'on peut atteindre sont celles données par un point d'un quart de de disque de rayon L relié au centre de ce quart de disque . Une autre chose à laquelle il faut faire gaffe : quand on fait glisser un bout de l'aiguille le long du bord en tournant autour d'un clou , l'autre extrémité ne décrit pas un cercle mais une courbe assez connue dont j'ai oublié le nom ( ce n'est pas beau de vieillir ) .

Ce travail peut "presque" se faire à la main mais si tu arrives à trouver les premières valeurs informatiquement avec ce schéma ou un autre  , ce serait un petit miracle .

J'espère que tout ça est à peu près compréhensible

Imod

PS  : pour être tout à fait rigoureux , chaque pente correspond à deux aiguilles : celle d'arrivée après la rotation ( qui n'en est pas vraiment une  ) et celle qui suit les translations ( où certains clous peuvent changer de côté ) .    

J'ai regardé L=5 et L=6 d'un peu plus près ( ne serait-ce que pour confirmer ou invalider des réponses informatiques ) .

Pour L= 5 , il me semble que contrairement à ce que j'avais affirmer ne passe pas mais passe ( et serait le meilleur ) , ce qui n'infirmerait pas la borne supérieure annoncée LittleFox et tant mieux .

Pour L= 6 , en utilisant la stratégie détaillée précédemment j'arrive à .

Tout ça est à prendre avec toutes les précautions d'usage , surtout à cette heure

Bonne nuit à tous .

Imod

Bonjour,
Je pense qu 'en observant les résultats "trouvés" on peut extrapoler une loi...

2	3	4	5	6
2	22	35/2	410/3	25

Sauf erreur pour L=7 , j'arrive à . On croit deviner une règle simple "pair-impair" .

Je crains que ce ne soit plus compliqué , mais on peut toujours espérer une heureuse surprise

Imod

Pour L=8 , . Apparemment ça confirme la règle bête "pair-impair"  , mais ce n'est que le début et sans aucune certitude

Imod

En fait en adoptant la stratégie que j'ai déjà explicitée on a pour L>3 :

si L est impair .

si L est pair .

Le plus pénible à gérer c'est le passage des clous d'un côté à l'autre de l'aiguille par glissement le long de l'axe .

J'ai vérifié "à la main" jusqu'à L=9 .

Il me semble qu'on doit pouvoir le confirmer ou l'infirmer informatiquement pour les premières valeurs mais rien ne garantit que cette stratégie est la meilleure ( j'ai quand même tendance à le penser ) .

Imod

Salut, j'ai enfin un programme qui semble marcher. Pour l'instant il ne fait que des rotations dans le sens trigonométrique mais les résultats sont plutôt cohérent avec ceux trouvés à la main.

 Cliquez pour afficher

from heapq import heappush, heappop
from collections import defaultdict

def nextMoves(L,a,g,d):
   gx,gy = g
   dx,dy = d
   assert(gy == 0)
   assert(gx < dx)
   
   # Move counter clockwise around g
   a_ = min(a,((dx-gx)**2+(dy-gy)**2)**0.5/(dx-gx)*dx)
   gx_,gy_ = gx,gy
   while True:
      bestg,bestd = None,None
      for x in range(1,gx_):
         y = gy_+(dy-gy_)*(x-gx_)//(dx-gx_)
         if bestg == None or (y-gy_)/(x-gx_) < (bestg[1]-gy_)/(bestg[0]-gx_):
            bestg = (x,y)
      for x in range(gx_+1,L):
         y = gy_+((dy-gy_)*(x-gx_)+(dx-gx_))//(dx-gx_)
         if bestd == None or (y-gy_)/(x-gx_) < (bestd[1]-gy_)/(bestd[0]-gx_):
            bestd = (x,y)
      if bestg != None and bestd != None and (bestg[1]-gy_)/(bestg[0]-gx_) < (bestd[1]-gy_)/(bestd[0]-gx_):
         gx_,gy_ = bestg
         continue
      dx_,dy_ = bestd
      break
   yield a_,(gx_,gy_),(dx_,dy_)
   
   # Move clockwise around g
   # TODO
      



def solve(L):
   start = ((1,0),(L-1,1),L)
   states = defaultdict(lambda : 0)
   stack = [(-start[2],0,start[0],start[1])]
   while stack:
      a,c,g,d =  heappop(stack)
      a = -a
      if states[(g,d)] >= a:
         continue
      states[(g,d)] = a
      if g[0] == d[0] or abs(d[1]-g[1])/(d[0]-g[0]) > a :
         yield a,c,g,d
         continue
      for a_,(gx_,gy_),(dx_,dy_) in nextMoves(L,a,g,d):
         heappush(stack,(-a_,c+1,(gx_,0),(dx_,dy_-gy_)))
         heappush(stack,(-a_,c+1,(L-dx_,0),(L-gx_,dy_-gy_)))

         
   

Dans le cas L=22 c'est au moment de passer la pente 1/4. La meilleure solution trouvée est de passer au milieu en (9,0),(13,1).
Dans le cas L=57 c'est au moment de passer la pente 1/5. La meilleure solution trouvée passe par (26,0),(31,1).

Bonsoir LittleFox et à ceux qui essaient de suivre ( ce problème n'est pas un cadeau ).

Les valeurs que j'avais proposées au delà de 9 n'étaient que des spéculations et j'étais quasiment certain quelles seraient mises en défaut à un moment ou un autre

En fait je suis plus intéressé par la stratégie à adopter pour retourner l'aiguille .

1°) Il me semble qu'on peut limiter les rotations au sens direct comme tu l'as fait .

2°) La succession des mouvements de l'aiguille se ferait dans l'ordre suivant :

       a) On fait glisser l'aiguille le long de son axe d'un bord à l'autre de façon à faire  
            passer le maximum de clous de l'axe vers le bord droit de l'aiguille .

      b) On fait tourner l'aiguille autour du premier clou dans le sens trigo en gardant
           l 'extrémité de l'aiguille en contact avec le bord .

Si on peut déjà admettre ces résultats , on limite énormément le champ des possibles .

On est vraiment tenté de choisir un clou central comme pivot et de centrer cette aiguille sur ce pivot avant de la faire tourner mais il me semble qu'ainsi on multiplie le nombre de cas à traiter et si on gagne sûrement en rapidité , je ne suis  pas sûr qu'on puisse alors retourner  une aiguille plus grande .

Ca fait beaucoup de suppositions et peu d'affirmations , il reste pas mal de grain à moudre .

Imod  





  

    

J'ai vérifié les valeurs fournies par LittleFox pour L=22 et L=57 et ça marche

Vu le peu de résultats établis , il est difficile de généraliser la formule .

On peut tout de même supposer que la taille de l'aiguille est de la forme  :

  avec  n entier et .

La valeur de n réalisant A(L) étant certainement bien plus proche de 2 que de L-2  , ce qui devrait permettre de lister les premières valeurs de A(L) dans un temps raisonnable .

Quelques centaines de valeurs de A(L) permettrait d'émettre des hypothèses . Informatiquement ça me semble réalisable car pour (L, n) donné le trajet de l'aiguille est imposé et relativement court .

Affaire à suivre , bien sûr toute aide est bienvenue

Imod

Purée, un mois plus tard

Bien sûr que ça marche, mon programme donne une solution. Mais sans garantie que c'est la meilleure.

Finalement,
Un problème simple,mais une formule alambiquée ,bravo à vous deux.

@LittleFox

Un mois c'est vraiment peu , si tu savais le nombre de problèmes que je traîne depuis  plus de trente ans  

Je n'ai pas grand chose à faire d'une garantie , mais une liste des premières valeurs de A(L) ( avec ton programme )  m'intéresse  beaucoup .

Imod

Voici quelques valeurs

 Cliquez pour afficher

 
 L    A(L)²   ~A(L)
 2     4/ 1  2.000000
 3     8/ 1  2.828427
 4    45/ 4  3.354102
 5   160/ 9  4.216370
 6    20/ 1  4.472136
 7   250/ 9  5.270463
 8   125/ 4  5.590170
 9    40/ 1  6.324555
10    45/ 1  6.708204
11   490/ 9  7.378648
12   245/ 4  7.826238
13   640/ 9  8.432740
14    80/ 1  8.944272
15    90/ 1  9.486833
16   405/ 4 10.062306
17  1000/ 9 10.540926
18   125/ 1 11.180340
19  1210/ 9 11.595018
20   605/ 4 12.298374
21   160/ 1 12.649111
22  2873/16 13.400093
23  1690/ 9 13.703203
24   833/ 4 14.430870
25  1960/ 9 14.757296
26  3825/16 15.461646
27   250/ 1 15.811388
28   272/ 1 16.492423
29  2560/ 9 16.865481
30  4913/16 17.523199
31  2890/ 9 17.919573
32  1377/ 4 18.553975
33   360/ 1 18.973666
34  6137/16 19.584752
35  3610/ 9 20.027759
36   425/ 1 20.615528
37  4000/ 9 21.081851
38  7497/16 21.646305
39   490/ 1 22.135944
40  2057/ 4 22.677081
41  4840/ 9 23.190036
42  8993/16 23.707857
43  5290/ 9 24.244129
44   612/ 1 24.738634
45   640/ 1 25.298221
46 10625/16 25.769410
47  6250/ 9 26.352314
48  2873/ 4 26.800187
49  6760/ 9 27.406406
50 12393/16 27.830963
51   810/ 1 28.460499
52   833/ 1 28.861739
53  7840/ 9 29.514591
54 14297/16 29.892516
55  8410/ 9 30.568684
56  3825/ 4 30.923292
57 24986/25 31.613921
58 16337/16 31.954069
59 26624/25 32.633725
60  1088/ 1 32.984845

Merci , ces valeurs confirment mes idées

Il y a clairement deux chaînes en fonction de la parité de L et les passages de à ou à , ... sont
facilement localisables de proche en proche sans passer par les déplacements de l'aiguille  .

Comme toi je ne suis pas sûr que cette stratégie soit la meilleure mais je vois ici deux belles suites à étudier  .

Je vais essayer d'y revenir dans moins d'un mois

Encore merci

Imod  

Je ne sais si on peut vérifier ça avec un logiciel mais si j'extrapole le tableau de LittleFox , j'arrive à un nouveau changement de pente  fatidique pour le cas pair avec L=116 ( passage de 1/4 à 1/6 ) et pour le cas impair  L=205 ( passage de 1/5 à 1/7 ) .

On peut calculer les valeurs suivantes avec  le même principe .

Je commence à croire que ce problème est un peu trop lourd

Imod

J'ai une formule générale pas trop lourde toujours en extrapolant le tableau précédent :

On note toujours L la largeur de la bande et A(L) la taille de la plus grande aiguille que l'on peut retourner dans cette bande .



Avec q le plus grand entier de la même parité que L et tel que ne dépasse pas L .



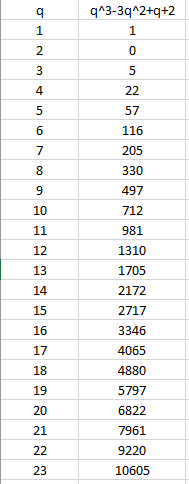
Par exemple pour une bande de largeur L= 23 on a q=3 et , on retrouve bien la valeur du tableau .

Bien sûr rien ne prouve que cette aiguille passe ni qu'on ne peut pas en faire passer une plus grande mais on peut s'essayer à valider ou détruire la formule pour quelques cas limites : avis aux amateurs

Imod

La réponse précédente est la bonne , j'ai une preuve complète que je développerais ultérieurement .

Imod

Une preuve complète?

Je n'ai pas oublié le problème , la solution est simple mais difficile à expliquer , j'y travaille

Imod

Je n'ai pas le courage de convertir la solution au format du forum

Imod