Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première DérivationTopics traitant de dérivation [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Dérivation 7''

Posté par
Mathes1 06-04-20 à 21:35

Bonsoir à tous ;
J'ai un petit exercice merci beaucoup d'avance !
Soit la fonction suivante ;
g(x)=\dfrac{1}{3}x3-x2+x-1
Étudier les variations de cette fonction et déterminer les Extremums s'ils existent
Alors je propose;
Dg=
Calculons g'
g'(x)=x2-2x+1
Dg'=
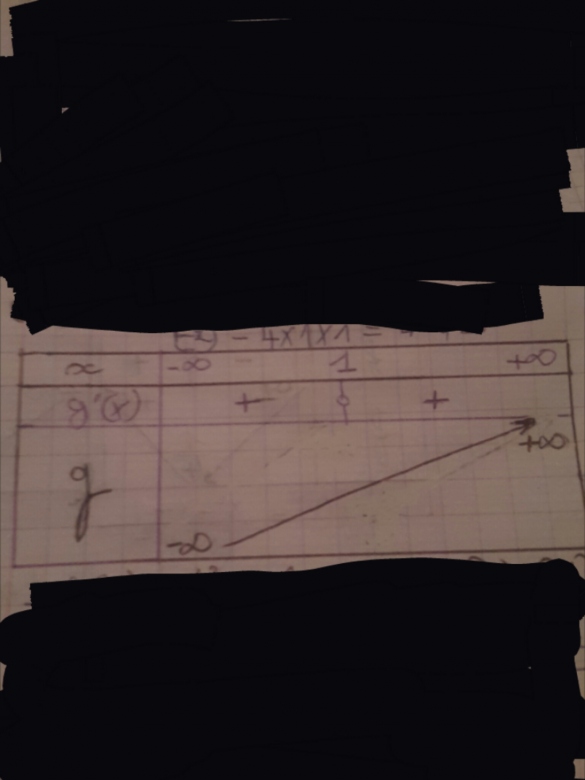
D'où le tableau des variations ;
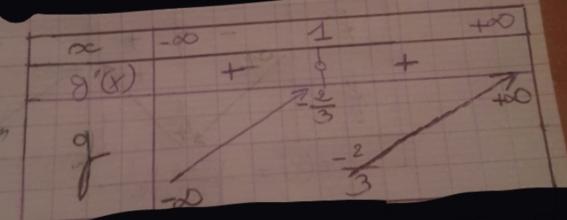
Dérivation 7\'\'
Merci beaucoup d'avance !

Posté par
Yzzre : Dérivation 7'' 06-04-20 à 21:37

Salut,

Justifie le signe de g'(x) ; et fais une seule flèche dans ton tableau de variations.

Posté par
heklare : Dérivation 7'' 06-04-20 à 21:38

Bonsoir

Pourquoi douter sur un tel exercice ?

Posté par
Mathes1re : Dérivation 7'' 06-04-20 à 21:52

Bonsoir ;
Merci beaucoup de m'avoir répondu !
Le signe de g'(x) est le signe de a après et avant les racines ( a=1>0)
La solution de l'équation g'(x)=0
est \boxed{x= 1}
Car :∆=0 donc cette équation admet une seul solution x=\dfrac{-b}{2a}=\dfrac{-(-2)}{2×1}=1
Comment on fait une seule flèche
Et on a \lim_{x\to +\infty } g(x)=+\infty
Et \lim_{x\to -\infty }g(x)=-\infty
Et g(1)=-\dfrac{2}{3}

Posté par
heklare : Dérivation 7'' 06-04-20 à 22:00

On ne prend pas un marteau-pilon pour écraser une mouche

g'(x)=(x-1)^2

On va de -\infty à +\infty  Il n'y a pas besoin de s'arrêter à 1

Posté par
Mathes1re : Dérivation 7'' 06-04-20 à 22:06

D'accord merci beaucoup à vous !

Dérivation 7\'\'

Posté par
heklare : Dérivation 7'' 06-04-20 à 22:10

Vous pouvez mettre  -\dfrac{2}{3} à cheval sur la flèche si vous voulez.

De rien

Posté par
Mathes1re : Dérivation 7'' 06-04-20 à 22:16

Dérivation 7\'\'
Est ce que c'est comme ça ?
Merci beaucoup à vous !

Posté par
heklare : Dérivation 7'' 06-04-20 à 22:18

Par exemple

Posté par
Mathes1re : Dérivation 7'' 06-04-20 à 22:19

"par exemple " c'est à dire correct ?
Bonne soirée !

Posté par
heklare : Dérivation 7'' 06-04-20 à 22:20

Oui bien sûr

Bonne soirée

Posté par
Mathes1re : Dérivation 7'' 06-04-20 à 22:40

Bonsoir ;.
Désolé j'ai oublié de répondre à
" Déterminer les Extremums s'ils existent"
x=1 est un minimum local.

Posté par
heklare : Dérivation 7'' 06-04-20 à 22:58

Il n'y a pas d'extremum  ni absolu ni local

Pour qu'il y ait un extrémum local la dérivée doit s'annuler en changeant de signe.Ce n'est manifestement pas le cas ici.


Rechercher
Menu
Espace membre
5 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1729 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !