bonsoir,

qu'as tu fait ?
que vaut f(a) ?
et f(a+h) ?

Leile
Je ne comprends pas que vaut h, on a la fonction mais h....
f(a) vaut 1/a non ?

excuse ma réponse tardive : ma connexion ne fonctionne pas bien ce soir.

f(a) = 1/a    c'est juste
h, c'est h.. c'est une constante, tu ne sais pas combien vaut h (une valeur très petite, mais inconnue).   On va garder h  comme ça.
f(a+h)   =    1 / (a+h)

à présent on peut écrire f(a+h) - f(a) =  1/(a+h)  -  1/a
mets sur même dénominateur, et simplifie.

Leile
1)
f(a+h) - f(a) = 1/(a+h)-1/a
f(a+h) - f(a) = 1/a+1/h-1/a ducoup on peut les 1/a et -1/a s'en vont :
f(a+h) - f(a) = 1/h
Question n°1 terminée...
2)
Le taux de variation c'est pas : (f(a+h)-f(a))/h ?
Ducoup ça ferrai : (1/h)/h Ducoup c'est égal à 1/h² non ?
3) Je sais pas comment expliquer mais je sais que si f(a+h) se rapproche de a alors la tangente qui symbolise a+h devient parallèles à la sécante de a ( elles se superposent et sont égales a peu près) j'arrive pas à bien expliquer mais je penses que c'est ça, je penses que vous voyez ce que je veux dire...
Y'a pas de soucis pour votre soucis d'internet
Je vous remercie

Leile

Q1)   tu t'es trompée, il fau tout mettre sur meme dénominateur



à présent reprends la question 2)
Le taux de variation c'est pas : (f(a+h)-f(a))/h ?  oui, c'est ça !
à toi !

Leile
Ducoup pour le taux de variation ça fait :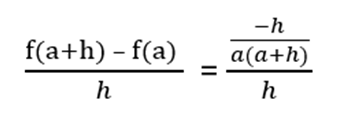



_{* Modération > Image recadrée car un peu encombrante *}

> malou edit > je t'ai mis le code de ta formule

Jam18, je vais te demander d'apprendre à utiliser les outils du site pour écrire les maths
choisis l'éditeur ltx


regarde un peu cette page explicative : [lien]

et pour t'aider à débuter, clique sur le code source des messages de Leile, pour voir comment elle a écrit (tu peux même faire des copier-coller en cas de besoin)


si tu n'as pas ce symbole, va dans ton espace membre, puis "préférences", coche "oui" pour "source accessible"

coucou malou !

Jam18
oui
et tu peux simplifier :



et pour diviser par une fraction, on multiplie par son inverse
donc tu obtiens ?

malou Bonjour madame j'arrivai pas bien à les utiliser merci
Leile qu'en pensez-vous ?

Jam18, tu ne simplifies pas suffisamment.
pour diviser par une fraction, on multiplie par son inverse  
tu le fais bien, mais là, tu peux tout de suite simplifier par h (qui est différent de zero)
==> tu obtiens tout de suite
-1 / (a(a+h))  
OK ?

q3)  quand h se rapproche de zero :   dans cette dernière expression, remplace h par 0.

bonjour Leile

en tout cas, bravo à Jam18 pour son essai d'écriture

coucou malou ; oui, tu as raison, Jam18 mérite un grand bravo !

Leile
Ah d'accord je comprends mieux donc je pars de :

ducoup on peut enlever le qui donne -1.
Ducoup ça fait bien comme vous dites  :



Q3) Pour cette question je remplace dans cette expression h par 0 ducoup ça fait =
Il me semble que ça doit avoir un lien avec f(a) =   mais ici je trouves
Qu'en pensez-vous ?

malou @ 30-10-2020 à 17:50

bonjour Leile

en tout cas, bravo à Jam18 pour son essai d'écriture

Q3)   taux(h) =   -1/a²       c'est juste !

q4)      justifier que f est dérivable sur R (est ce que ça n'est pas plutôt sur R*  ?   donc sauf pour x=0 ?

comment fais tu pour cette question ?

exprimer f'(a)   ou exprimer f'(x) ?

Leile
Pour la question 3 j'ai trouvé mais qu'est ce que je peux en déduire ?

f est dérivable si la limite du taux d'accroissement quand h tend vers 0, est une valeur finie.
ici, tu as vu que le taux est égal à  -1/a²  quand h tend vers 0 : c'est donc une valeur finie (tu peux la calculer pour toute valeur de a différente de zero).
Ainsi, f est dérivable sur R*

f'(a) =  -1/a² , tu l'as bien noté.

la dérivée de f(x) = 1/x,   c'est   f'(x) = -1/x²

OK ?

Leile
Je n'ai pas encore vu mais qu'est-ce qu'une valeur finie ?
Ducoup la dérivé de f(a) =1/a est f'(a) = -1/a² car on veut f'(a) ce qui revient au même.

Aussi pour la question n°3 : que peut-on en déduire, je mets seulement le résultat -1/a² ?? Je comprends pas je dois en déduire quoi ? J'ai le résultat mais la déduction?

une valeur finie : comme je te l'ai dit, c'est une valeur que tu peux calculer, qui n'est pas infinie.
Si ta limite est l'infini, la fonction n'est pas dérivable.

la dérivé de f(a) =1/a est f'(a) = -1/a²   ==> oui.

3) Que peut-on dire de taux(h) lorsque h devient de plus en plus proche de 0?
on peut dire qu'il est égal à -1/a², et donc qu'il est calculable.
la limite du taux quand h tend vers 0 est finie (pas infinie).
d'accord ?

Leile
" Et donc il est calculable" je ne comprends pas qui est il et comment on le calcul du coup vu qu'il est "calculable".
Une valeur infinie par exemple : 1/3a ?
Désolé de poser ce genre de question mais je cherches à comprendre, comme j'ai déja dit j'ai eu seulement qu'1h sur ça...

Sinon j'ai un deuxième exercice sur les dérivés, je le poste ici ou je le met sur une  nouvelle page ?

nouvel exercice ---> autre sujet à ouvrir

malou
Excusez-moi mais vous avez oublié ma de répondre à ma question ( avant dernier message )

c'était volontaire, je vais laisser Leile répondre
si tu n'as pas de réponse cet AM, remets un message, je lirai tout pour te répondre

Jam18

si tu donnes une valeur à    a    (différente de 0),  tu peux calculer le rapport   -1/a², n'est ce pas ? ce rapport est calculable : tu obtiens une valeur précise, on dit qu'elle est finie.

Quand on regarde la limite du taux quand h tend vers 0, si la limite est l'infini (+oo   ou -oo), alors la limite n'est pas finie, et la fonction n'est pas dérivable.

Ici, si a = 0,  la limite de -1/a²   est   -oo,   donc  la fonction n'est pas dérivable en 0.
mais pour toute autre valeur de a, tu peux calculer précisemment cette limite
'exemple si a=1, tu calcules   -1/a² = -1), donc la fonction est dérivable pour toute valeur de R sauf 0 (remarque que ta fonction 1/x  n'était pas non plus définie sur R  mais sur R*).

NB : 1/3a  est calculable, si a est différent de 0. Si a est grand, tu trouveras une valeur très petite, mais une valeur précise quand même.

tu peux regarder cette fiche : Cours sur les dérivées et la dérivation

est ce que c'est plus clair  pour toi ?

Leile
Oui tout est clair merci beaucoup
Une dernière question, j'ai déterminer que f est dérivable en f'(a) c'est bien ça ?
Vous pouvez me donner un exemple de valeur infinie svp ?

Leile @ 31-10-2020 à 13:27

Jam18

si tu donnes une valeur à    a    (différente de 0),  tu peux calculer le rapport   -1/a², n'est ce pas ? ce rapport est calculable : tu obtiens une valeur précise, on dit qu'elle est finie.

Quand on regarde la limite du taux quand h tend vers 0, si la limite est l'infini (+oo   ou -oo), alors la limite n'est pas finie, et la fonction n'est pas dérivable.

Ici, si a = 0,  la limite de -1/a²   est   -oo,   donc  la fonction n'est pas dérivable en 0.
mais pour toute autre valeur de a, tu peux calculer précisemment cette limite
'exemple si a=1, tu calcules   -1/a² = -1), donc la fonction est dérivable pour toute valeur de R sauf 0 (remarque que ta fonction 1/x  n'était pas non plus définie sur R  mais sur R*).

NB : 1/3a  est calculable, si a est différent de 0. Si a est grand, tu trouveras une valeur très petite, mais une valeur précise quand même.

tu peux regarder cette fiche : Cours sur les dérivées et la dérivation

est ce que c'est plus clair  pour toi ?

Jam18, il est inutile de citer mes messages.

j'ai déterminer que f est dérivable en f'(a) c'est bien ça ?
non, tu as determiné que f(a) est dérivable sur R*, et donc pour toute valeur de a différente de zero.
Pour toute valeur de a différente de zéro, tu peux calculer f'(a).

NB : quand j'ai dit  "le rapport", j'aurais pu dire "la fraction"..

Dans la suite du cours, tu verras que
la limite du taux de variation entre a et (a+h) te donne le nombre dérivé ; c'est la valeur de f'(a).
C'est aussi le coefficient directeur de la tangente à la courbe au point d'abscisse d'équation y=mx+p.
un coefficient directeur m ne peut pas être égal à l'infini : la droite est alors parallèle à l'axe des ordonnées et son équation est sous la forme x=c
Donc il faut que cette limite soit différente de l'infini, pour que f soit dérivable.
Mais là, on anticipe un peu..

Leile
J'avais j'avais citer un de vos messages pour que vous comprenez plus facilement ma question.
Je vous remercie beaucoup de votre aide
Bonne fin de vacances

oui, je comprends ; pour plus de lisibilité (et moins de perte de place), tu peux juste écrire
"voir votre message du 31 à 13:27", ou juste rappeler quelques mots..
Tu peux garder le "citer"   quand on est nombreux sur le  sujet, et qu'un rappel du pseudo ne suffit pas. Tu vois ?
En tous cas, je vois que tu as pris latex en main rapidement : bravo !

Je suis désolée d'avoir souvent répondu avec retard : j'ai des soucis de connexion depuis quelques jours.. Si on se retrouve une prochaine fois, ce sera certainement plus rapide !
Bonne fin de WE à toi aussi.