Inscription / Connexion Nouveau Sujet
Des segments tortueux
Bonjour tous,
Nous avons une période de segments...
Soit une belle grille de 10x10
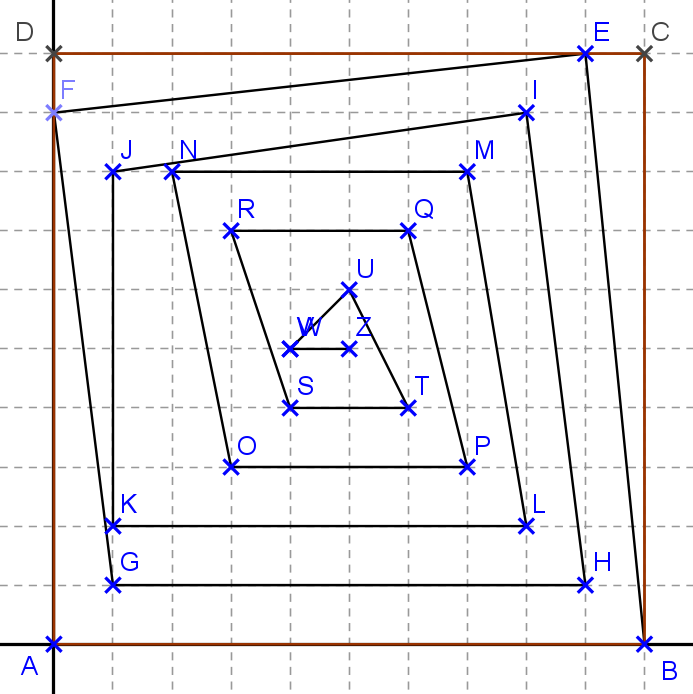
Quel est le plus grand nombre de segments attenants de longueur différente que vous pourrez trouver.
Attention :
Aucun point ne peut se placer à une distance égale à la longueur d'un segment déjà trouvé ...
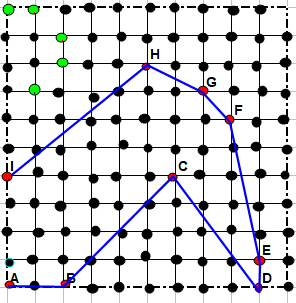
Je donne un exemple de départ
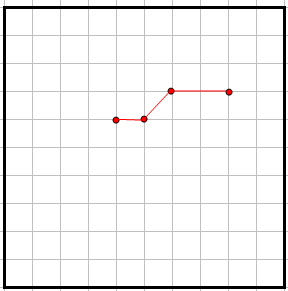
Bonjour Dpi
Pendant la recherche sur le problème précédent , j'étais tombé sur un lien proposant une spirale :

Je ne sais pas si ça correspond exactement au cadre de ton problème 
Imod
Magnifique spirale!
Combien de segments de celle-ci dans une grille de 10x10 ?
A priori 7.
Il y a mieux 
Dans la spirale d' Imod il y a aussi une distorsion (volontaire ou non) :5 devrait être plus à gauche d'une case (2x2 ) avant (2x3 )
On note aussi que 0->3 = 4-->5.
Ce qui donne une variante à mon problème:
version1 / les segments sont comptés dans l 'ordre 0-->1-->2 -->3 etc..
et on ne tient pas compte des segments induits tels que 0-- >2ou 0-->3 ou 1-->3
version 2/ on tient aussi compte des longueurs induites (dans cette version on ne doit plus avoir de segments  5 ou
5 ou
 10
10 13
13
salut
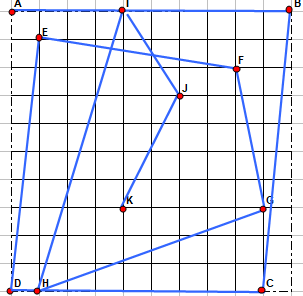
je propose un truc comme :
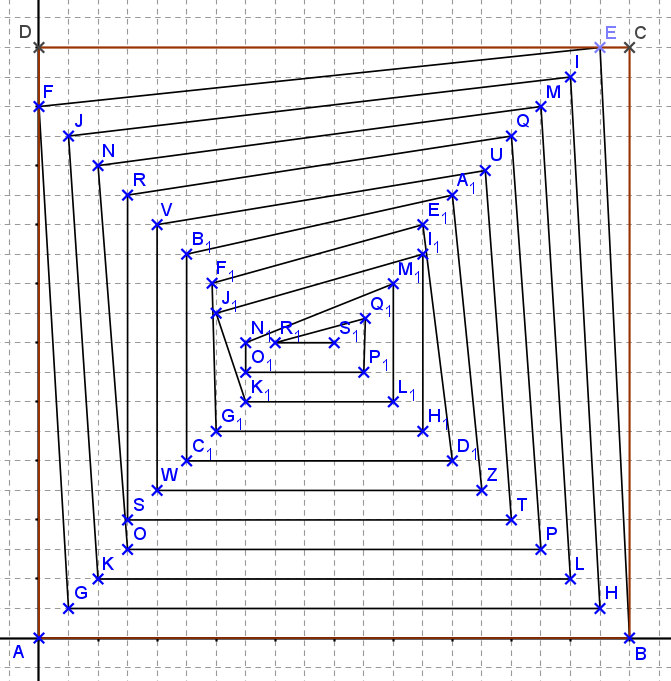
attention :
1/ je n'ai pas été le plus efficace au sens où comme par exemple G1 n'appartient pas au segment [B1C1] et j'aurai pu faire de même avec I1
2/ je n'ai pas vérifié que les distance était toute distincte
c'est simplement pour donner une idée du principe et une autre idée serait le tapis de Sierpinski ... en partant du centre ou d'un coin ...
bon ce n'est pas la bonne figure (toujours ce pb de réactualisation du cache ou je ne sais quoi ...)
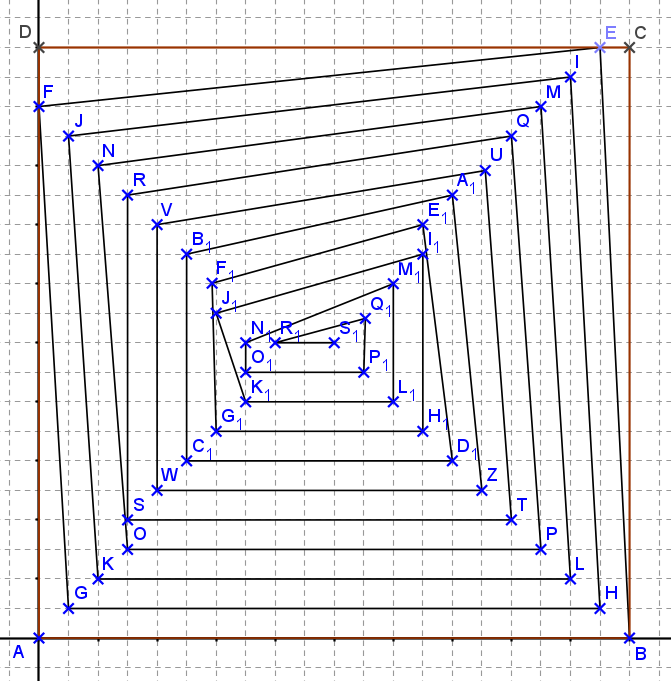
désolé !! il semble que ce soit moi qui ai fait une fausse manip ... 
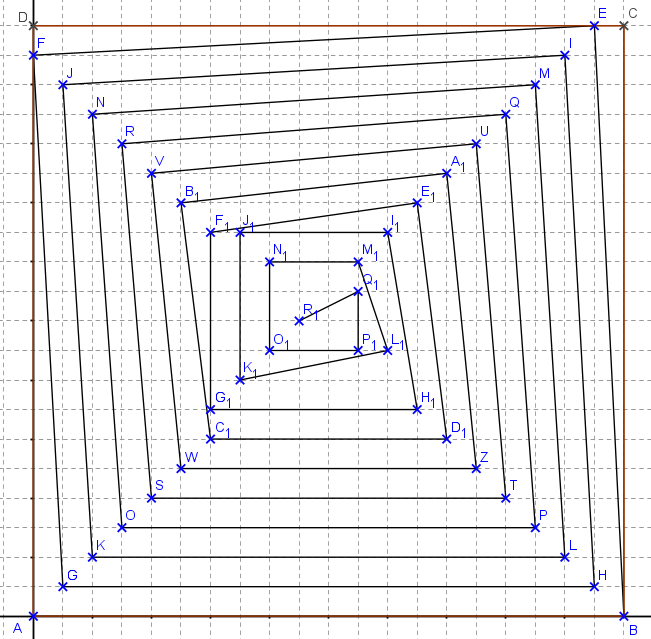
voila la bonne image
pour mon point 2) de mon premier msg : en particulier en connaissant le théorème des deux carrés et les entiers somme de deux carrés de différentes façons
donc il faut vérifier que toutes les distances sont bien distinctes 
PS : la modo peut donc effacer mon 2e et 3e msg ...pour ne pas surcharger le fil, merci par avance 
Bien.
Mon exercice initial était la version 2.
La spirale d'Imod a initié la version 1
Le résultat de carpediem est imbattable après la remarque de derny
Il reste à trouver la version 2
Aucun segment induit ne doit se retrouver par exemple DF KG et une multitude de  2
2
Pour ton travail rien à dire :segments tous de longueurs différentes.
L'autre version est beaucoup plus sournoise
FG =3 impossible car BF=3 .
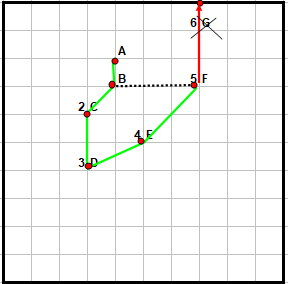
On peut donner les résultats actuels...
On devrait arriver presque à la moitié de l'alphabet de carpediem
Je déconseille de partir par les petits segments car les segments "induits" augmentent très vite 
trop "compliqué" : non seulement il faut "compter" le segments déjà tracés mais en plus il faut "compter" les segments non tracés et pour chaque point ajouté il "apparait" n - 1 segments à calculer ... 
J'étais parti 4 jours ,je croyais avoir des réponses 
J'ai une solution à 11 segments.
Qui trouvera mieux
Toujours rien...
Quelques astuces:
*essayer le plus possible d'éviter le parcours du cavalier (aux échecs) car il élimine 8 points proches.
*le parcours des segments peut se croiser
*éviter les parcours parallèles espacés de 2,4 ou6 colonnes ou lignes
en effet plus aucun point ne sera possible au milieu (symétrie ) .
*un damier peut être utile .
Rebonjour
Trop occupé par ailleurs je n'ai absolument pas suivi le fil et du coup je ne comprend plus la où les questions . Je résume ce que j'ai cru comprendre , on corrigera au besoin :
On cherche un chemin qui est une ligne brisée dont les sommets sont les 121 nuds d'une grille 10X10 . Comme pour tous les chemins ( simples ) , la ligne ne doit jamais repasser par un même sommet . Celle-ci peut tout de même couper une ligne déjà tracée ( en dehors des nuds ? ) mais aucun des segments de la ligne ne peut avoir la même longueur .
Sur la grille il y a 110 longueurs différentes .
Imod
Bonne lecture
*Dès qu'un segment est tracé il faut éliminer tous les symétriques.
*retarder le plus possible 2x1 .
*les points candidats fondent comme neige au soleil 
Je viens de relire l'ensemble du fil et pour tout dire , c'est toujours aussi obscur 
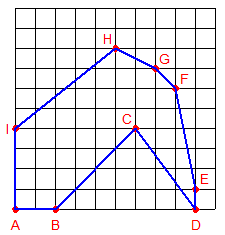
Si j'ai bien compris ton illustration , tu autorises le point E et pourtant EC=ED mais tu interdis le point G car FB=FG . Je suis sans doute mauvais lecteur mais il faut poser les règles clairement sinon chacun y va de son couplet et plus personne ne comprend personne . Après il ne faut pas s'étonner de l'absence de réponses . J'essaie de préciser le problème comme je l'ai compris , si ce n'est pas ça , il n'est pas utile de me demander de relire le fil mais simplement de préciser la demande .
On considère les ensembles de points aux nuds d'une grille 10X10 tels qu'aucun cercle centré sur un point de cet ensemble ne contient plus d'un point de l'ensemble . On cherche le cardinal maximal de ces ensembles . Après il me semble que vu le peu de contraintes sur le chemin celui a de bonne chance de se faire tout seul .
Imod
Rien ne t'échappe en effet mon petit exemple aurait du déjà finir au point E d'autant plus que je dis plus loin qu'il faut éviter les segments du type CD .
Comme j'ignore le score maximum ,j'encourage les participants à
proposer leur réponse.
Je ne comprends toujours pas tes règles 


Pour moi ta ligne brisée s'arrête au point D car AB=AD . En fait tu exposes ta stratégie en long en large et en travers sans vraiment expliquer les règles du jeu , c'est assez pénible 
Si par hasard j'ai compris quelque chose , tu auras beaucoup de mal à tracer 11 segments 
Imod
Je fatigue (c'est l'âge et la chaleur ).
J'ai donné une mauvaise version ...mais tu as compris le principe.
Je vois que tu as bouclé le parcours ce qui n'est pas interdit.
Sauf erreur ,ma solution à 11 segments peut passer à 12 en bouclant.
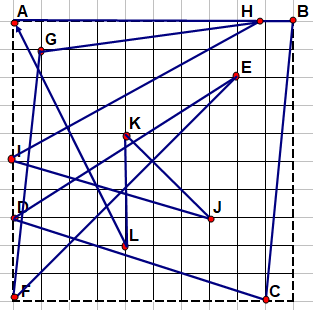
En fait j'ai pointé la différence entre ton problème et celui que j'avais proposé . Je vais proposer une nouvelle version qui rejoindra sans doute la tienne .
PS : Je n'ai pas vérifié ta solution mais je te fais confiance . Il me semble qu'avec un peu d'adresse on doit pouvoir éviter les croisements qui rendent la lecture difficile 
PPS : J'espère que tu te souviens que je suis toujours un peu bourru mais jamais méchant 
Imod
Oui (ça me poursuit depuis le début )
Entre temps j'ai modifié 
il me semble que 11 est imbattable ...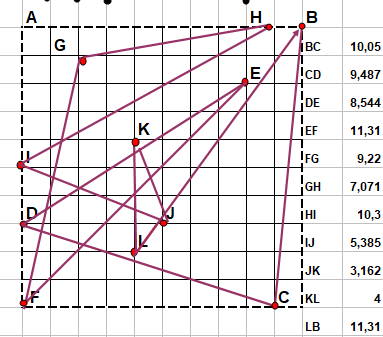
En fait je pense qu'on doit pouvoir faire mieux ca je m'étais imposé des contraintes bien trop fortes . On peut déjà tracer 6 segments dans une grille 5X2 .
Imod
PS : DJ=DK , le fameux 4²+3²=5²+0² 
Une remarque j'ai déjà du faire , seuls les points importent . Il n'est pas interdit de tracer des segments pour ajouter de la lisibilité mais dans ce cas autant le faire proprement c'est à dire sans croisement . Tu aurais pu par exemple tracer le polygone BECFDLJIKGH .
Imod
Effectivement le polygone que tu me conseilles convient et possède
10 segments.
On attend toujours un record 
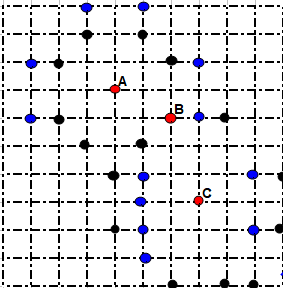
J'ai repris mon image avec 9 points et les grosses contraintes , il peut servir de point de départ pour aller plus loin .
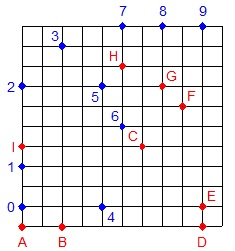
Les 10 points bleus sont les seuls qui peuvent être ajoutés à la figure , après chaque point choisi va en disqualifier d'autres . Ce qui est sur c'est qu'on peut en ajouter au moins un . Il n'y a bien sûr aucune raison que cette démarche aboutisse au maximum de points possibles .
Je crois de plus en plus que les segments troublent le problème 
Imod
Je pense que la réponse viendra de mon fil , patience .
Imod
Je ne pense pas, non. Dans ton fil on ne compare que les segments ayant un sommet en commun. Ici c'est les segments du chemin par rapport à tous les autres segments.
C'est quand même très différent.
J'avoue ne plus rien comprendre à ce fil 
S'il s'agit d'interdire les distances égales entre deux points quelconques , j'ai donné la réponse qui est 9 ( c'est une conséquence immédiate du fil précédent ) .
Imod
En effet cet exercice est déroutant ,c'est d'ailleurs son "charme"
Si on reprend ton canevas ,seuls les points verts sont candidats ,en
effet tous les points noirs éliminent les positons déjà marquées et leurs segments induits.
Dans les éliminations il y bien sûr les pièges :
0²x5² =3²x4² 1²x7² =5²x5² 1²x10² =6²x8² 1²x8² =4²x7² et 2²x9² =6²x7²
Tout ça pour dite qu'un petit programme informatique
devrait arranger les choses .
Je suis persuadé que nous viendrons à bout de ce problème
Mon système d'élimination par point se complique très vite .
Mon pronostic est 10 et par miracle 11 segments.
Comme le dit Imod, le chemin le plus long contient 9 segments (10 si on accepte les cycles) si chaque segment doit avoir une longueur unique parmi toutes les paires de sommets.
En effet, le plus petit carré avec 10 sommets est de côté 11 et le plus petit pour 11 sommets est de côté 13 ![]() . Nous avons un carré de côté 11.
. Nous avons un carré de côté 11.
Il n'y que deux ensembles de sommets possibles avec 10 sommets dans un carré de 11 de côté.
Pour chacun de ces ensembles, il suffit d'ordonner les sommets pour avoir un chemin. Par exemple:
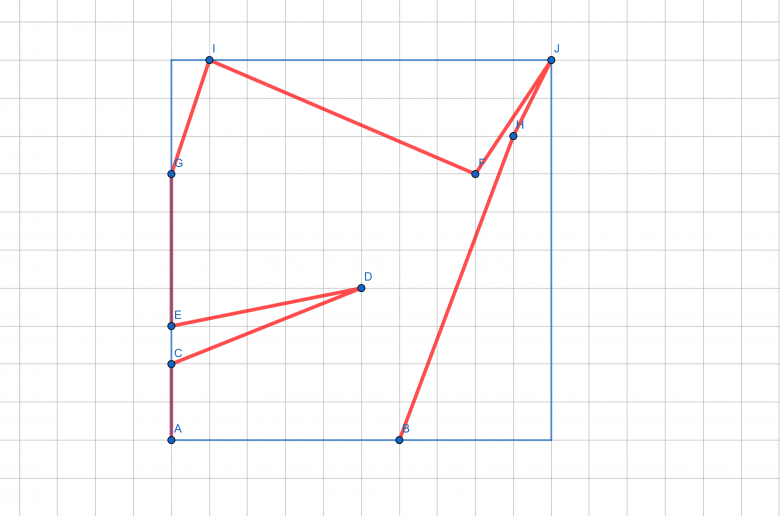
@dpi
Du coup, il doit y avoir une erreur dans ton candidat le 27-08-25 à 11:15.
En effet, la solution de Imod est correcte mais les candidats de dpi sont faux. En fait il n'y a plus d'autres candidats:
 Cliquez pour afficher
Cliquez pour afficherLe code utilisé pour la vérification:
 Cliquez pour afficher
Cliquez pour afficherNote: Ce code est loin d'être efficace, on revérifie l'ensemble des points pour chaque candidats.
Il reste à attendre une réponse au problème comme je l'avais compris et elle viendra de l'autre fil 
Croiser les fils c'est bien quand on fait de la tapisserie mais sur un forum c'est l'enfer . J'imagine quelqu'un qui revient de vacances et qui lit ça 


Imod
Oui, comme moi qui découvre les discussions depuis hier 
Est-ce que tu saurais mettre le lien quand tu dis "l'autre fil" ou "mon fil". Ça aiderait le futur lecteur à naviguer 
En fait la source est ici ![]() Diamètre d'un ensemble varié et la suite j'ai proposé avec ce que j'avais cru comprendre à la variante de Dpi
Diamètre d'un ensemble varié et la suite j'ai proposé avec ce que j'avais cru comprendre à la variante de Dpi
![]() Points acceptables . Je ne suis pas sûr que chacun y retrouvera ses petits mais les références sont là
Points acceptables . Je ne suis pas sûr que chacun y retrouvera ses petits mais les références sont là 
Imod
Je pense que je dois enterrer mon fil 
Dommage car il pouvait faire un beau jeu de société sur un damier:
Exemples
1/quel est le plus mauvais début (éliminant le plus de candidats )?
2/quel est la plus mauvaise situation à 3 points .
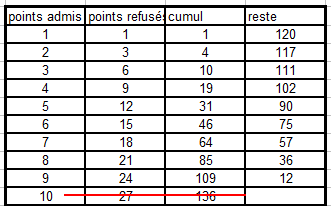
Avec l'expérience on constate qu'on élimine en moyenne* 3 candidats par coup, nombre qui se cumule.
Il n'est pas donc étonnant qu'on bute sur 10.
*approximation
 Cliquez pour afficher
Cliquez pour afficherOn peut tout de même donner la meilleure réponse avec la règle que deux points ne peuvent pas être à la même distance d'un troisième :
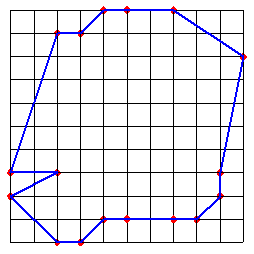
J'ai utilisé le c(17) de LittleFox sur l'autre fil 
Imod