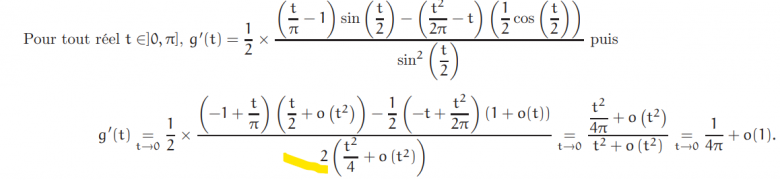
Bonjour,

C'est une erreur.

On peut le montrer en calculant par exemple avec t = 10^-3 (petit)

La ligne du haut donne :

g'(t) = 1/2 * [10p^-3/Pi - 1) * ...  = 0,159... (à la calculette)

Alors que 1/(4Pi) = 0,0795... (ligne du bas)
*****
Si on vire le 2 souligné en jaune, alors on retombe sur ses pieds dans les valeurs calculées.

Et à mon avis, la raison pour laquelle ce 2 est là, c'est qu'au lieu de calculer , l'auteur a voulu faire le malin avec le DL de cos



Les sont faux, c'est qui est attendu dans le dernier facteur des deux dernières lignes de calcul!

C'est à dire on va avoir différents résultats selon le DL utilisé?

La limite que tu trouves à la fin ne doit jamais changer, mais rien ne t'empêche de pousser les DL au rang 17 dans les calculs intermédiaires si ça te chante.

Mais plus tu fais de calculs, plus tu risques de te tromper, comme dans mon exemple ci dessus où on a vite fait d'oublier un facteur 1/2 si on est distrait

Ahh je viens de comprendre ce que vouz vouliez dire, j'ai oublié le facteur 1/2  dans mon calcul comme dans votre exemple , merci infiniment .

J'ai eu le nez creux
De rien