Inscription / Connexion Nouveau Sujet
diagramme de venn
bonjour, aidez-moi svp, je ne comprend rien!
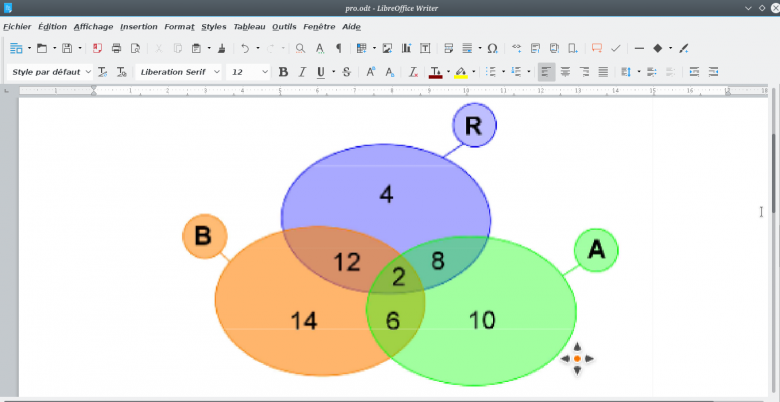
Dans l'association sportive d'un lycée plusieurs activités sont proposées aux 100 élèves adhérents et parmi elles le badminton (B), l'aviron (A) et le roller derby (R).
Le diagramme de Venn ci-dessous donne les nombres de participants à ces trois activités:
(Voir la photo)
On choisit un adhérent au hasard. Calculer:
1. la probabilité qu'il ne pratique aucun des trois sports cités ci-dessus.
2.La probabilité qu'il pratique l'aviron.
3.La probabilité qu'il pratique le badminton et le roller derby.
4.La probabilité qu'il pratique le roller derby ou l'aviron.
5.La probabilité qu'il pratique deux des trois sports mais pas les trois.
J'ai vraiment besoin d'aide svp! je ne comprend pas.
Merci de votre compréhension!
Bonjour
le diagramme montre que sur les 100 élèves du Lycée il y en a
4 qui pratiquent le roller et aucun autre sport
12 qui pratiquent le roller et le badminton
8 qui pratiquent le roller et l'aviron
et 2 qui pratiquent les trois sports
et donc en tout ça fait 4+12+8+2 = 26 qui pratiquent le badmington avec ou sans d'autre(s) sport(s)
etc.
il n'y a qu'à lire et faire quelques additions ...
seule formule à appliquer : nombre de cas favorables/nombre de cas possibles
en sachant que le nombre de cas possibles est 100
après tu comptes sur ton dessin !
Bonjour!
Pouvez-vous me dire si c'est bon ou pas?
ps: je viens de commencer la leçon donc c'est normal si je ne comprends pas!
1- P(ne pratique aucun des trois sports) = 4/100+10/100+14/100=24/100=0.24.
2- P(pratique l'aviron) = 10/100
3-P(pratique le bad et le roller derby)= 12/100.
4-P(pratique le roller derby ou l'aviron) = 8/100.
5-P(pratique deux des trois sports mais pas les trois) = 2/100.
tout est faux
c'est pas un problème de leçon mais de bon sens sur la lecture du diagramme et la compréhension de phrases en français, le sens de "et" et de "ou" etc.
1 tu as calculé ceux qui pratiquent un sport et un seul quel qu'il soit
2 tu as calculé ceux qui ne pratiquent que l'aviron
3 il n'est pas dit ceux qui pratiquent le bad et le roller uniquement
il faut ajouter ceux qui pratiquent les trois sports
4 tu as calculé ceux qui pratiquent le roller et l'aviron uniquement
5 ce que tu dis est ceux qui pratiquent les trois sports !
Bonjour,
Désolé mais tes réponses sont fausses.
Je reprends la première question posée :
1- P(ne pratique aucun des trois sports) = 4/100+10/100+14/100=24/100=0.24.
Tu as pris en compte :
* les 4 élèves qui pratique le roller exclusivement c'est à dire le roller mais pas les 2 autres sports.... donc ces 4 élèves pratiquent bien un sport : le roller !
* de même pour les 10 élèves pratiquant uniquement l'aviron
* idem pour les 14 élèves pratiquant uniquement le badminton.
Ces 28 élèves ne pratiquent qu'un seul sport mais ils pratiquent un sport ! Ils n'entrent donc pas dans la catégorie des élèves qui ne pratiquent aucun des trois sports cités.
Les élèves qui ne pratiquent aucun des 3 sports cités, ne peuvent pas être dans les parties colorées.... As tu calculé le nombre des élèves présents dans les parties colorées ??
1- P( pratique aucun des trois sports) = 4/100*14/100*10/100=560/1000000.
2- P(pratique l'aviron)= 10/100*2/100=20/10000.
3- P(pratique le bad et le roller) = 14/100*4/100*10/100=560/1000000.
4-P(roller ou l'aviron) = 8/100*2/100=16/1000
5-P(pratique deux des trois sports mais pas les trois)= 1-P(A)+P(B)+P(R) = 1- 14/100+10/100+4/100
= 27/100
des produits, ça ne tient pas debout.
tu dois commencer par raisonner en termes de nombres de participants et c'est tout
et ensuite à partir du nombre de participants tu calcules des probabilités.
un produit de nombres de participants, ça ne rime à rien.
il est facile de trouver le nombre de participants qui pratiquent effectivement au moins une activité : c'est juste la somme de tous les nombres qui sont inscrits dans le diagramme ! simple bon sens de base.
et ceux qui ne pratiquent aucun sport, c'est le reste sur les 100 en tout.
J'ai fais ça mais je sais que c'est pas bon! Mais je comprends pas!
1- P(pratique aucun des trois sports) = 12/100+8/100+6/100
2- P(pratique l'aviron) = 6/100+8/100= 14/100
3- P(pratique le badminton et le roller derby) = 12/100+8/100+2/100= 22/100
4- P(pratique le roller ou l'aviron) = 8/100 +2/100=10/100
5-P(pratique deux des trois sports mais pas les trois) = 1-12/100+8/100+6/100
= 25/100
??
arrête de considérer ça comme des probabilités composées (ça te rend stupide) et considères cela comme cela doit être réellement : des nombres effectifs de participants et du simple BON SENS
des exemples je t'en ai déja donné dans mon premier message
ça c'est le calcul effectif pour la question 1 = te faire ton exo :
le nombre de participants qui pratiquent effectivement au moins une activité :
c'est juste la somme de tous les nombres qui sont inscrits dans le diagramme ! simple bon sens de base.
tu ne comprends pas ce que veut dire "au moins une activité" ?
et que c'est exactement le contraire de "aucune activité" ?
"tous les nombres qui sont inscrits" ??
et la somme c'est 4+12+2+8+4+6+10 = ... (tu sais faire une addition tout de même ?)
et donc ceux qui restent, ceux qui ne pratiquent aucune activité, c 'est 100 moins ça
et donc la probabilité cherchée c'est ce nombre de participants là divisé par 100 inscrits en tout
Non, tout est faux.
Oublie pour l'instant les probabilités et essaye simplement de comprendre le diagramme...
Il te faut comprendre la signification des différentes parties du diagramme. C'est du simple bon sens comme t'a dit Mathafou.
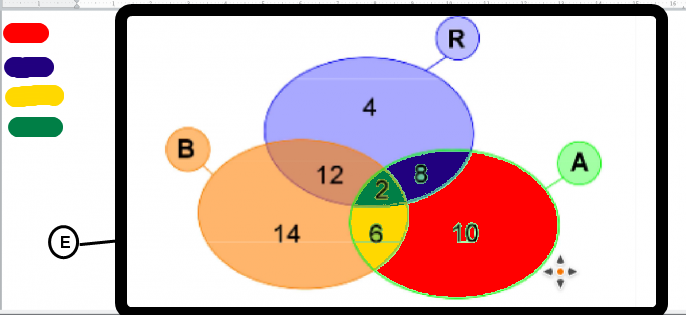
J'ai "repeint"  quatre parties de ton diagramme. Pourrais tu pour chacune de ces 4 parties (rouge, bleu, jaune et verte) dire en les détaillant, les sports pratiqués par les élèves qui y sont comptabilisés ?
quatre parties de ton diagramme. Pourrais tu pour chacune de ces 4 parties (rouge, bleu, jaune et verte) dire en les détaillant, les sports pratiqués par les élèves qui y sont comptabilisés ?
Les 10 élèves de la partie rouge pratiquent......... (donc un seul sport)
Les 8 élèves de la partie bleue pratiquent........ (donc deux sports)
Les 6 élèves de la partie jaune pratiquent......... (donc deux sports)
Les 2 élèves de la partie verte pratiquent......... (donc ??? sports)
Non, tout est faux.
Oublie pour l'instant les probabilités et essaye simplement de comprendre le diagramme...
Il te faut comprendre la signification des différentes parties du diagramme. C'est du simple bon sens comme t'a dit Mathafou.
J'ai "repeint"
 quatre parties de ton diagramme. Pourrais tu pour chacune de ces 4 parties (rouge, bleu, jaune et verte) dire en les détaillant, les sports pratiqués par les élèves qui y sont comptabilisés ?
quatre parties de ton diagramme. Pourrais tu pour chacune de ces 4 parties (rouge, bleu, jaune et verte) dire en les détaillant, les sports pratiqués par les élèves qui y sont comptabilisés ?
Les 10 élèves de la partie rouge pratiquent......... (donc un seul sport)
Les 8 élèves de la partie bleue pratiquent........ (donc deux sports)
Les 6 élèves de la partie jaune pratiquent......... (donc deux sports)
Les 2 élèves de la partie verte pratiquent......... (donc ??? sports)

Les 10 élèves de la partie rouge pratiquent l'aviron
Les 8 élèves de la partie bleue pratiquent l'aviron et le roller
les 6 élèves de la partie jaune pratiquent l'aviron et le bad
les 2 élèves de la partie verte pratiquent 1 des ces activités ? ou bien aucun de ces activités?
j'ai fais quelque chose pouvez- vous corriger ?? je ne sais pas si c'est bon mais j'ai tenter !!!
1)4/100+8/100+12/100+2/100+14/100+6/100+10/100 = 56-100=44.
2) 10/100+6/100+2/100+8/100 = 26/100
3) 14/100+12/100+4/100 = 30/100
4) 10/100+8/100+4/100 = 22/100
5) 6/100+8/100+12/100 = 26/100.
Les 10 élèves de la partie rouge pratiquent l'aviron OUI
Les 8 élèves de la partie bleue pratiquent l'aviron et le roller OUI
les 6 élèves de la partie jaune pratiquent l'aviron et le bad OUI
les 2 élèves de la partie verte pratiquent 1 des ces activités ? ou bien aucun de ces activités? FAUX
Si on considère ces 2 élèves,
* ils appartiennent à l'ensemble A donc ils font de l'Aviron
* ils appartiennent à l'ensemble R donc ils font aussi du Roller
* et ils appartiennent à l'ensemble B donc ils font de plus du Badminton
donc ces 2 là, pratiquent l'Aviron et le Roller et le Bad (donc les 3 activités citées).
Le sous ensemble vert est A R
R  B
B
pouvez-vous me dire si c'est bon ?
1)4/100+8/100+12/100+2/100+14/100+6/100+10/100 = 56-100=44. ( je sais que ce n'est pas bon! comment je fais ?)
2) 10/100+6/100+2/100+8/100 = 26/100
3) 14/100+12/100+4/100 = 30/100
4) 10/100+8/100+4/100 = 22/100
5) 6/100+8/100+12/100 = 26/100.
j'ai fais quelque chose pouvez- vous corriger ?? je ne sais pas si c'est bon mais j'ai tenter !!!
1)4/100+8/100+12/100+2/100+14/100+6/100+10/100 = 56-100=44. FAUX et les dernières égalités sont.... ridicules

2) 10/100+6/100+2/100+8/100 = 26/100 OUI
3) 14/100+12/100+4/100 = 30/100 FAUX
4) 10/100+8/100+4/100 = 22/100 FAUX
5) 6/100+8/100+12/100 = 26/100. OUI !! une lueur d'espoir....
Un peu dommage que tu t'entêtes à écrire des probabilités......
déja en écrivant les calculs que l'on fait correctement
une telle écriture fait dresser les cheveux sur la tête
(quelle que soit la signification de ce calcul il est totalement faux dans son écriture)
4/100+8/100+12/100+2/100+14/100+6/100+10/100 = 56-100=44
56-100 est un nombre négatif ! (donc forcément différent de 44)
et de toute façon il n'est pas égal à 4/100+8/100+12/100+2/100+14/100+6/100+10/100
(et pour la signification d'un tel calcul, des centièmes d'élèves je ne sais pas ce que c'est)
j'ai fais quelque chose pouvez- vous corriger ?? je ne sais pas si c'est bon mais j'ai tenter !!!
1)4/100+8/100+12/100+2/100+14/100+6/100+10/100 = 56-100=44. FAUX et les dernières égalités sont.... ridicules

3) 14/100+12/100+4/100 = 30/100 FAUX
4) 10/100+8/100+4/100 = 22/100 FAUX
Un peu dommage que tu t'entêtes à écrire des probabilités......
[/vert]
Expliquez moi comment je dois faire pour les trois la parce que je suis complètement perdue !

Si tu as fait la 5, tu devrais pouvoir faire la 3... essaye. Il faut dénombrer les élèves qui pratiquent le badminton et le roller derby (sous entendu et RIEN d'autre donc pas de 3ème activité !!).
Pour la 4., il faut dénombrer les élèves qui pratiquent le roller derby ou l'aviron donc tous ceux qui ont dans leur liste d'activités ces 2 sports. On comptabilise en conséquence,
1) ceux qui pratiquent uniquement le Bad (une seule activité le Bad)
2) ceux qui pratiquent uniquement le Roller (une seule activité le Roller)
3) ceux qui pratiquent ces deux activités donc le Bad et le Roller
N'as tu jamais entendu parler de l'intersection de 2 ensembles ? de la réunion de 2 ensembles ?
Pour la 1) réponds à la question posée dans l'un de mes premiers messages :
Les élèves qui ne pratiquent aucun des 3 sports cités, ne peuvent pas être dans les parties colorées.... As tu calculé le nombre des élèves présents dans les parties colorées ??
1) P (ne pratique aucun des trois sports ) = 14/100+10/100+4/100 = 28/100-1= 27/100
3) P(pratique le bad et le roller derby) = 14/100+4/100 = 18/100.
4) P(pratique le roller ou l'aviron) = 10/100+4/100 = 14/100.
Si c'est pas bon je sais pas!
J'ai des grosses difficultés en maths donc voilà ! 
Si au lieu de tenter ta chance en espérant un miracle, tu voulais bien être un peu ATTENTIF à ce que l'on te dit.... on t'a dit d'oublier pour l'instant les probabilités !!
Arrête de faire du copier-coller puis du bricolage aberrant ("28/100-1= 27/100" c'est du niveau 4ème... et tu es en première !).
Prends un papier, un crayon et décortique (décompose) le diagramme qui t'est donné... fais un dessin avec seulement A et R : deux "patates" qui ont une partie commune (comme sur le diagramme) ; et exprime chaque partie avec des mots.... (voir ci dessous)
Ensuite j'essaie de te guider en te posant des questions et tu fais comme si tu n'avais pas vu. La différence entre ET et OU, c'est du français, pas vraiment des maths.
1) La probabilité qu'il ne pratique aucun des trois sports cités pour moi il serait dans le rond noir non ?
désolant en première d'écrire des calculs comme un mauvais élève de 5ème n'oserait même pas le faire !!
et tu ne comprends même pas que ce que tu écris est absurde et ne veut rien dire du tout
rien que dans son écriture même
tu ne sais pas que le signe "=" en mathématique veut dire que les deux choses qui sont de part et d'autre sont égales ???
et absolument rien d'autre
et surtout pas "exécuter le calcul précédent et continuer un autre à partir de ce résultat là"
28/100 (le résultat de ta somme) n'est pas égal à 28/100-1 qui est écrit juste après !
on ne peut pas écrire des calculs de cette façon !!
on doit le faire sur des lignes séparées
..+...+... = 28/100
puis je fais un autre calcul (sur une autre ligne) : 1 - 28/100 = ...
indépendamment de la justesse de ces nombres, je te parle de la façon d'écrire des calculs en général. et ce depuis le tout début de tes études (en primaire ?)
***citation inutile supprimée***
Oui je savais qu'il faut écrire de la sorte dans mes calcule mais quand je suis au brouillon!!! j'écris comme ça pour allez plus vite car je ne crois pas que quand je suis dans un devoir j'aurais le temps d'écrire au brouillon égal a ligne!!! et je n'aime pas la façon dont vous me parlez c'est pas en parlant de la sorte que vais apprendre quelque chose je suis désolé d'écrire comme cela mais j'ai toujours écrit mes calculs AU BROUILLON comme ça et aucun de mes professeurs mon réprimander de la sorte! Je suis désolé de vous répondre comme cela moi j'ai juste demander de l'aide car j'ai mal AVEC LA COMPRÉHENSION DES SUJET EN MATHS et que j'aurais besoin d'aide mais si vous me parlez de la sorte je ne crois pas que je m'en sortirais !!!
Encore désolé de vous parlez comme cela mais personne ma jamais parler comme ça même pas mes parents alors j'aimerais que vous parler d'une autre manière s'il vous plaît!
ENCORE DÉSOLÉ!!!
Désolée d'écrire comme sa!!!!!
Mais s'il vous plaît éviter de parler comme ceci à ma fille elle a simplement demander de l'aide car elle a dû mal avec la compréhension des sujets !!
écrire comme ça même au brouillon donne des calculs faux. point barre.
il faut perdre cette habitude AU PLUS VITE et définitivement
ce n'est certainement pas plus long d'écrire proprement que d'écrire des calculs faux parce que les opérations qu'on devrait faire sont à l'envers !!
1 - 28/100 n'est pas la même chose que 28/100 - 1 !!
"l'énervement" vient de ce que c'était déja dit
alors quand il faut le répéter ... çà prouve qu'on ne lit même pas ce qu'on dit!
1)4/100+8/100+12/100+2/100+14/100+6/100+10/100 = 56-100=44. FAUX et les dernières égalités sont.... ridicules

déja en écrivant les calculs que l'on fait correctement
(quelle que soit la signification de ce calcul il est totalement faux dans son écriture)
alors quand on recommence à écrire ensuite de telles absurdités faut pas pousser...
allez, je vous laisse avec votre croyance qu'en écrivant comme un cochon au brouillon ça va faire gagner du temps et aboutir à des calculs justes ...
Restons calmes 
Voici une autre présentation des données.
Dans la colonne "effectifs", j'ai mis toutes les valeurs numériques figurant sur le diagramme. A chaque fois je me suis demandé quel est ou quels sont les sports pratiqués par les élèves correspondants.
Comprends tu ce tableau ?


Elle (fille de la Réunion), nous a quitté pour d'autres rivages..... où elle a abordé il y a 2 heures avec le même sujet et les questions 2 et 5 correctement traitées 
Elle n'est donc pas venue sur notre île pour rien.
Trop drôle. Le monde est si petit....
Bonjour excusez-moi j'ai eu le même devoir et malgré vos indication je n'y arrive pas
d'après votre tableau pour la question 1) le calcule serai : P(pratique aucun des trois sports) = 10+4+14+6+2
= 44 ?
3) P(pratique le badminton et le roller derby) = 12+2
= 14
4) P(pratique le roller derby ou l'aviron) = 8+2
=10






