Cliquez pour afficherOn estime la somme des aires des rectangles min et max, et on en déduit que la somme ne peut être qu'un carré parfait compris entre le min et le max.
Cela conduit à seulement 3 possibilités pour la somme des surfaces des rectangles, soit 121 , 144 et 169 … donc des carrés de cotés 11 , 12 ou 13
On cherche alors toutes les combinaisons qui permettent cela, on trouve 35 possibilités.
14 pour S = 121, 9 pour S = 144 et 12 pour S = 169
Sauf erreurs voici ce que cela donne :
S = 121
Possibilité 1: [(1, 6), (2, 9), (3, 10), (4, 8), (5, 7)]
Possibilité 2: [(1, 6), (2, 10), (3, 8), (4, 9), (5, 7)]
Possibilité 3: [(1, 6), (2, 10), (3, 9), (4, 7), (5, 8)]
Possibilité 4: [(1, 7), (2, 10), (3, 6), (4, 9), (5, 8)]
Possibilité 5: [(1, 8), (2, 6), (3, 10), (4, 9), (5, 7)]
Possibilité 6: [(1, 8), (2, 7), (3, 10), (4, 6), (5, 9)]
Possibilité 7: [(1, 8), (2, 9), (3, 7), (4, 6), (5, 10)]
Possibilité 8: [(1, 8), (2, 10), (3, 5), (4, 9), (6, 7)]
Possibilité 9: [(1, 9), (2, 7), (3, 6), (4, 10), (5, 8)]
Possibilité 10: [(1, 9), (2, 7), (3, 8), (4, 6), (5, 10)]
Possibilité 11: [(1, 9), (2, 7), (3, 10), (4, 5), (6, 8)]
Possibilité 12: [(1, 9), (2, 8), (3, 6), (4, 7), (5, 10)]
Possibilité 13: [(1, 10), (2, 5), (3, 9), (4, 8), (6, 7)]
Possibilité 14: [(1, 10), (2, 8), (3, 7), (4, 5), (6, 9)]
****************
S = 144
Possibilité 1: [(1, 3), (2, 9), (4, 10), (5, 7), (6, 8)]
Possibilité 2: [(1, 3), (2, 10), (4, 7), (5, 9), (6, 8)]
Possibilité 3: [(1, 3), (2, 10), (4, 8), (5, 7), (6, 9)]
Possibilité 4: [(1, 5), (2, 6), (3, 8), (4, 10), (7, 9)]
Possibilité 5: [(1, 7), (2, 4), (3, 8), (5, 9), (6, 10)]
Possibilité 6: [(1, 7), (2, 9), (3, 5), (4, 6), (8, 10)]
Possibilité 7: [(1, 9), (2, 5), (3, 7), (4, 6), (8, 10)]
Possibilité 8: [(1, 9), (2, 6), (3, 5), (4, 7), (8, 10)]
Possibilité 9: [(1, 10), (2, 4), (3, 5), (6, 8), (7, 9)]
****************
S = 169
Possibilité 1: [(1, 2), (3, 5), (4, 9), (6, 10), (7, 8)]
Possibilité 2: [(1, 2), (3, 7), (4, 6), (5, 10), (8, 9)]
Possibilité 3: [(1, 2), (3, 7), (4, 9), (5, 6), (8, 10)]
Possibilité 4: [(1, 2), (3, 8), (4, 5), (6, 10), (7, 9)]
Possibilité 5: [(1, 3), (2, 5), (4, 8), (6, 9), (7, 10)]
Possibilité 6: [(1, 3), (2, 7), (4, 5), (6, 10), (8, 9)]
Possibilité 7: [(1, 3), (2, 7), (4, 8), (5, 6), (9, 10)]
Possibilité 8: [(1, 4), (2, 5), (3, 7), (6, 9), (8, 10)]
Possibilité 9: [(1, 5), (2, 3), (4, 9), (6, 7), (8, 10)]
Possibilité 10: [(1, 5), (2, 4), (3, 8), (6, 7), (9, 10)]
Possibilité 11: [(1, 5), (2, 7), (3, 4), (6, 8), (9, 10)]
Possibilité 12: [(1, 6), (2, 3), (4, 8), (5, 7), (9, 10)]
************
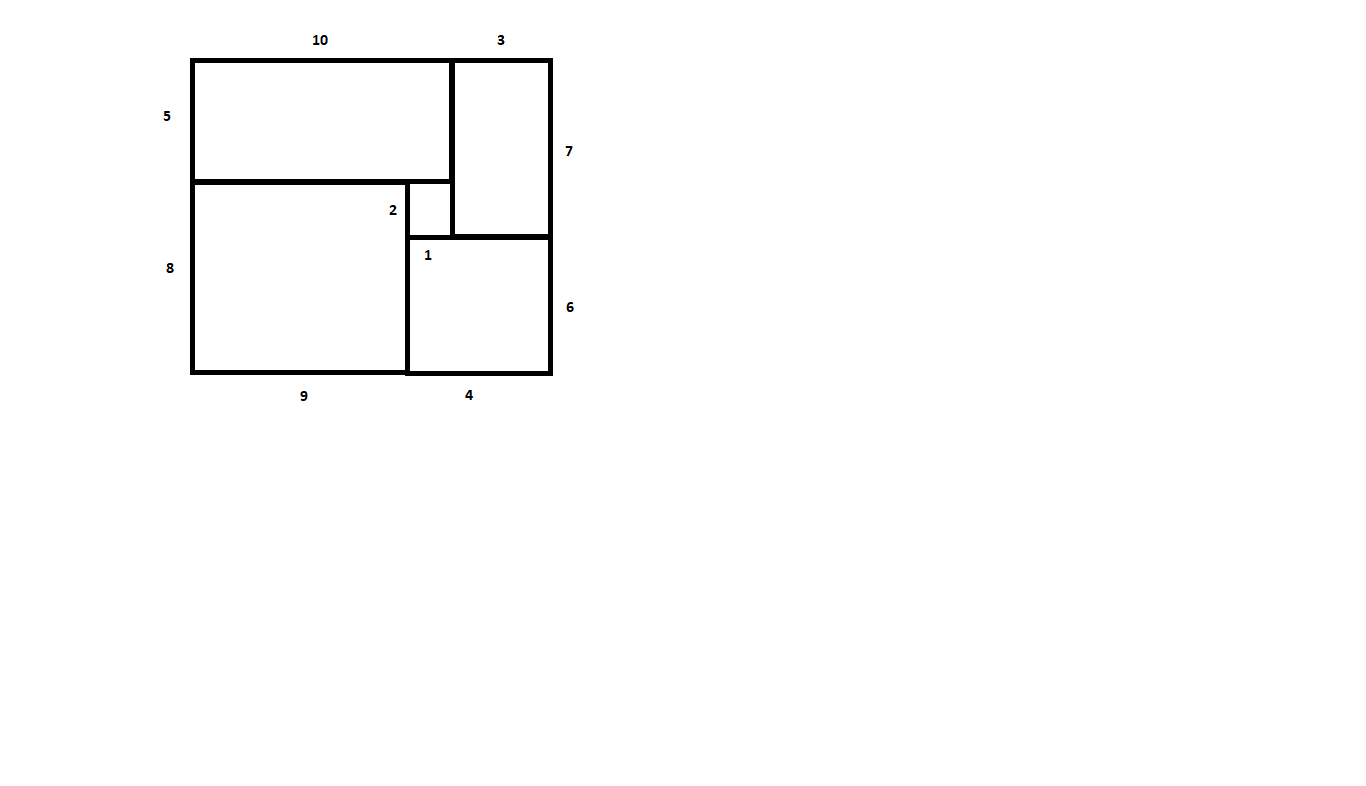
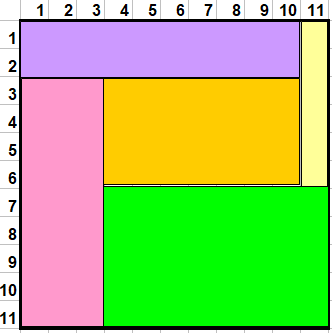
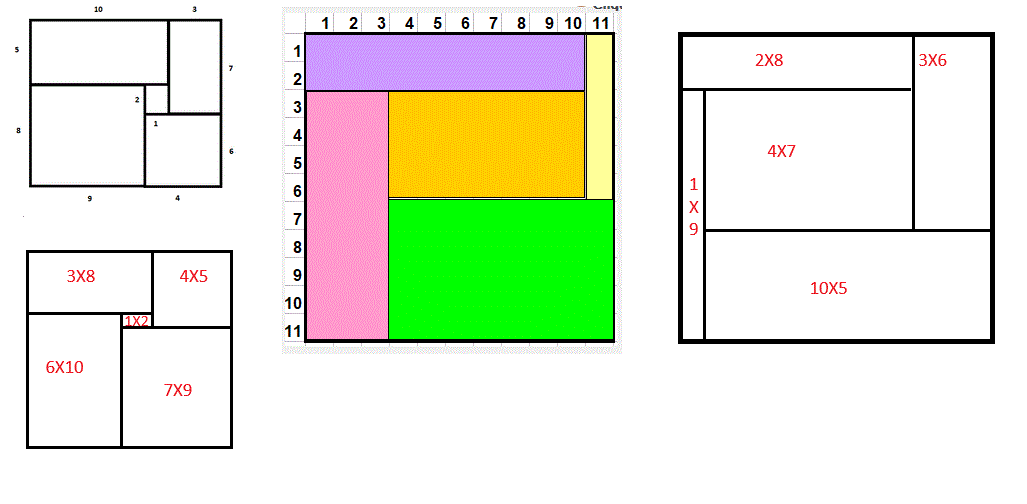
Il faut encore trouver si parmi ces 35 possibilités certaines permettent d'assembler les 5 rectangle pour formé un carré sans trou et sans recouvrement. Et c'est là que cela devient plus ardu.
On peut facilement supprimer une bonne quantité de possibilités, surtout celles qui comportent de grands rectangles qui rendent impossibles le positionnement des autres.
Exemple évident, le rectangle (9,10) placé dans le carré empêche le positionnement du rectangle (5,7) …
Quand on a supprimé toutes ces possibilités impossibles de manière évidente, il en reste à peu près une moitié … et là, je n'ai pas de vraie tactique pour tester les possibilités restantes. En y allant donc à tâtons, il me semble qu'il ne reste plus aucune possibilité.
Donc, ma réponse est pas de solutions.
Mais il y a probablement plus "mathématique" pour réaliser la fin du tri des possibilités et s'assurer que je n'ai pas loupé une solution
Annuler
connectez vous