Inscription / Connexion Nouveau Sujet
DM de maths dérivation
Bonjour,
Je n'arrive pas a terminer mon DM vous pourrez m'aidez s'il vous paît?
J'ai fait toute la question 1 et le 2 petit a
L'énnocer c'est :
1. On considère la fonction g définie sur 
par g(x)=x3-3x-3.
a. Etudier les variation de gsur
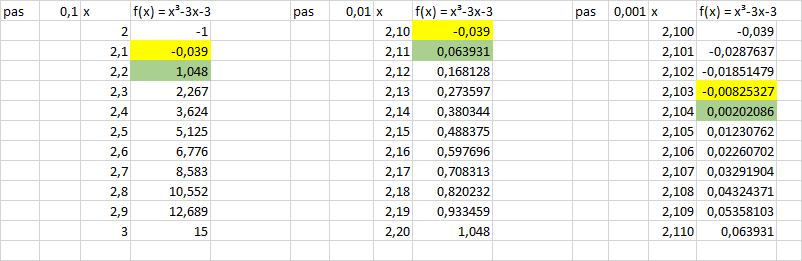
b. Démontrer que l'équation g(x)=0 admet une unique solution que l'on notera 
. Donner un encadrement à 10-2 prés de .
c. Déterminer le signe de g(x) sur
2. soit f la fonction définie sur ]1;+
[ par f(x)= (2x3+3)/(x2-1) et C sa courbe représentative dans un repère du plan.
a. Déterminer l'expression de f'(x), pour tout x dans ]1;+[
b. Expliquer pourquoi, sur ]1;+[, f'(x) et g(x) ont le mêm signe.
c. En déduire le sens de variation de f sur ]1;+[
d. En utilisant la définition de , montrer que f()=3. En déduire un encadrement du minimun de f
e. On considére la droite D d'équation y=2x. Etudier la position relative de C et de D.
f. Déterminer l'abscisse du ou des points de la courbe C où la tangente ets parrallèle à la droite D.
Bonjour,
Pour la 2 b. :
sur ]1;+[, f'(x) et g(x) ont le même signe.
vérifions d'abord ce que tu as trouvé pour... f '(x)
Nous sommes d'accord 
donc pour traiter la question 2 b., il faut essayer de faire apparaître dans l'expression de f'(x), l'expression de g(x) !! ce qui n'est pas très difficile.
Coup de pouce : factorise le numérateur de f '(x)
Comment faire pour répondre à la question 2d)
j'ai trouver environ 1.32 pour à la question 1b)
Est ce que je dois le réutiliser ou non?
Mais pour la question 2 d) le
c'est le résultat que j'ai trouver à la question 1 b?Oui bien sûr.
j'ai trouver environ 1.32 pour à la question 1b)
Moi pas
As tu regardé histoire de vérifier, ce qu'il se passe graphiquement ?
bonjour à vous deux,
je ne fais que passer
pour le cas où il y aurait confusion : pour la question 2d),
il s'agit en effet du de la question 1b),
mais il ne faut pas utiliser la valeur approchée pour répondre à la question, il faut garder pour montrer l'égalité f()= 3
Alors où en es tu avec cette valeur approchée de ?
Comment as tu procédé ??
d. En utilisant la définition de
, montrer que f()=3. En déduire un encadrement du minimun de f On a donc g(
) = 0 (ça doit servir à un moment ou à un autre !!)
J'ai (faute de mieux... qui existe peut-être ?) calculé f(
) -3... avec l'espoir de trouver 0 !! car si f()-3 =0, alors je pourrai conclure que.....
@ carita bonsoir,
Merci pour ton intervention qui complète ce que j'ai dit à Léalia26.
Pour la 2 d., j'aurais aimé trouver un passage permettant d'aller directement de f() à 3.... je n'ai pas trouvé.
Donc j'ai utilisé f() -3... comme dit ci dessus !Je pense être resté dans les clous puisque l'énoncé donne en fait la réponse 3.
bonsoir ZEDMAT
montrer que f()-3=0 est à mon avis la meilleure façon de faire (= la plus simple et la plus rapide), puisque l'énoncé nous indique ce 3, donc on en profite
sinon, plus lourd, exprimer ³ et ² à partir de l'égalité g()=0, injecter dans f(), simplifier... bof, je préfère ta méthode !
je te laisse poursuivre tranquillement.
bonne soirée !
Annuler
connectez vous