Inscription / Connexion Nouveau Sujet
Dm Dérivation
Bonjour, j'ai un dm de math a faire pour la rentre et j'ai un peu de mal.
Voici l'énoncé :
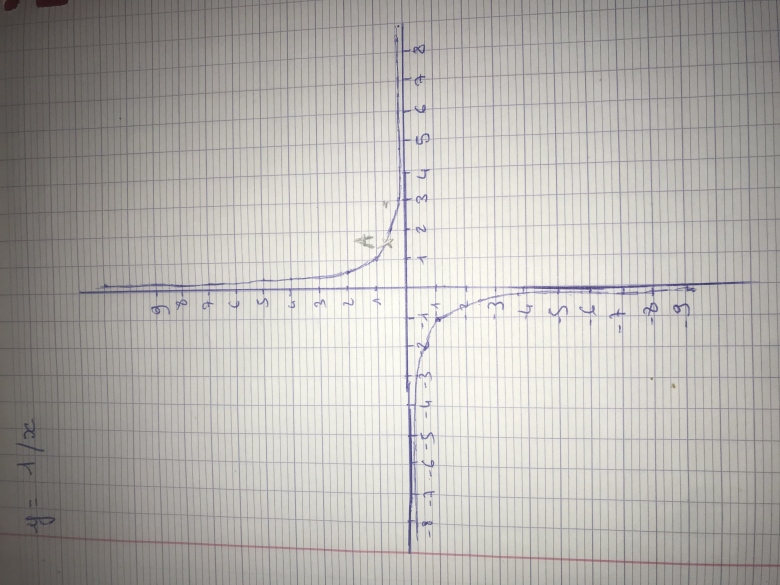
Dans un repère donné, on considère l'hyperbole d'équation : y=1/x.
1) Montrer, qu'au point A d'abscisse 3/2 l'hyperbole admet une
tangente de pente (-4/9).
( j'ai fais la première question ci dessous )
2) Déterminer l'équation réduite de cette tangente.
( Pour la deuxième question grâce au à la pente de À on place un deuxième point que je nomme B, grâce à cela on peut tracé la tangente et donc lire les coordonne de À et de B ) —> je ne suis pas sûr pour cette question, es-ce la bonne méthode ?
3) Démontrer que cette tangente coupe chacun des axes du repère en un point. On les
nomme B et C.
( je n'ai pas trouvé, j'ai du mal)
4) Montrer que le point A est le milieu de [BC].
Merci, d'avance !
Bonjour
Vous savez que le nombre dérivé en est le coefficient directeur de la tangente au point d'abscisse
à la courbe représentative de
Soit le cours soit équation d'une droite dont on connaît un point et le coefficient directeur
Intersection avec les axes
Axe des ordonnées
Axe des abscisses
Oui, pour la question 1, la tangente est dérivable au point A , de pente (-4/9).
Pour la deuxième question, on a donc A d'abscisse 1,5, mais pas son ordonné donc comment faire ?
y= 0,4x+p. A(..... ; 1,5 )
Si vous voulez construire la tangente en A à la courbe il est peut-être implicite que le point appartient à la courbe
Ne prenez pas des valeurs approchées. Ce n'est pas la tangente mais la fonction qui est dérivable en .
Cette valeur est celle de l'abscisse du point pas son ordonnée
Ainsi, pour montrer montrer qu'au point A d'absicce 3/2 l'hyperbole admet une tangente de pente (-4/9), il ne faut pas montrer graphiquement mais algébriquement avec la formule de la tangente ?
Car lorsque j'ai placé le point A d'abscisse 3/2, par rapport à ce point j'ai trouvé une pente de -0,4 ( en avançant de 1 et je suis descendu de -0,4)
1) Je dirais : la courbe ayant une tangente en son point d'abscisse 3/2 , la pente de cette tangente peut être déterminée à partir de l'équation y = 1/x de la courbe.
Ouii, c'est en résumé ce que je voulais dire pour la première question, merci !
Ainsi pour la deuxième : Déterminer l'équation réduite de cette tangente.
Je pensais grâce à la pente de À qu'il fallait place un deuxième point pour tracer la tangentes, et donc utiliser la formule y=mx+p.
Mais enfaite, il faut uttiliser la formule de tangente, y= f'(a)(x-a)+f(a).
Ainsi y= f'( 3/2 )(x- (3/2) +f(3/2)
y= 2( x-3/2) + 0,4
y= 2x-3+0,4
y= 2x- 13/5
Es-ce cela ?
Euh oui..
Donc qu'est-ce qui ne vas pas dans mon calcule d'au dessus ?
Je me rectifie...
C'est bien y= f'(3/2)(x-(3/2))+f(3/2)
y=2x-3-0,4
y= -4/9x-17/5
??
La 1ère ligne est juste.
La 2ème ligne ??
La 3ème est juste sauf l'ordonnée à l'origine qui ne l'est pas.
Oui je me suis trompé, j'ai mal écrit.
Ainsi je me suis trompé sur le résultat du coef directeur :
y=f'(3/2)(x-3/2)+f(2/3)
y= -4/9x-35/12 (ou bien -19/12)
Cette foi ci c'est le bon ?
Oui c'est ce que j'ai fait au-dessus est donc je vous ai demandé si le coefficient directeur est bien -19/12 ?
Euh . . .
y = f '(3/2)(x - 3/2) + f(3/2)
y = - 4/9(x - 3/2) + 2/3
y = - 4/9x + 4/9*3/2 + 2/3
y = - 4/9x + 4*3/(9*2) + 2/3
y = tu pourras peut-être finir . . .
Ah enfinnn mdr.
Par contre pour la troisième question j'en ai aucune idée, on avait vu aucune démonstration en cours.
Oui.
Or ce point appartient à la tangente. L'équation de celle-ci te donnera donc l'abscisse du point.
L'équation de la tangente est y = - 4/9x + 4/3 .
On cherche l'abscisse de son point d'ordonnée nulle.
Il faut donc remplacer y par 0 .
Si c'est bon j'ai compris :
-4/9x+4/3=0
-4/9x=-4/3
x= 13/4
Ainsi son ordonné est nulle est son abscisse est 13/4.
Donc la tangente coupe l'axe du repère en deux point B(0) et C( 13/4)


