Inscription / Connexion Nouveau Sujet
Domaine de définition
Bonjour!
Alors je suis en train de réviser mes mathématiques pour mon prochain contrôle qui portera sur les fonctions de références.
Et en particulier sur le domaine de définition.
Je voudrais savoir si vous pouviez par exemple me donner un ou plusieurs exercices à faire ici sur l'île qui porte sur la recherche du domaine de définition d'une fonction, en particulier la fonction inverse, carré et racine carré et la fonction affine.
Je n'ai pas trouvée d'exercices où l'on me demandait de trouver le domaine de définition...
J'espère que vous aurez compris ce que j'ai écrit..
Merci infiniment.
Maria.
Mais en fait c'est ce que je demande, je ne trouve pas d'exo sur le domaine de def et je voulais savoir si vous en aurez en tête où si vous sauriez quel type d'exo je pourrais faire...
Bonjour hekla, merci pour les sujets.
Pour le 1)
(4x+1)/(2x-1)
Il faut pas que ca soit égal à 0.
Donc: 2x-1=0 / 2x=1 / x=1/2 R-1/2 ou ]-infini ; 1/2 [ U ] 1/2 ; + infini [
Bon pour le premier?
Pour le 2eime je ne suis pas sûr, mais j'ai essayée.
(x^2+3x-1)/(x^2-5)
Là aussi il ne faut pas que ce soit égal à O.
Donc on fait c+d=0
x^2-5=0 / x^2=5 / x= + ou - Racine de 5
Je crois que c'est pas bon...
1 bien
2 bien
il ne faut pas que ce soit égal à O.
il faut dire : «il ne faut pas que le dénominateur soit égal à 0»
puis calculons les valeurs qui annulent ce dénominateur
3 on ne peut prendre la racine carrée que d'un nombre positif donc résolvons
Ah je pensais c'était faux ce que j'avais fait..
Tant mieux!
Donc pour le 3° avec la racinne carré comment est ce que je fais?
Je résous l'équaton meme si il ya la racine?
un nombre positif n'est pas un nombre nul
la quantité sous la racine (ou radicande) est
elle doit être positive donc
à résoudre
Mais vous savez j'y ai pensée cela ma semblait bizarre!
Bon je continu alors:
+ ou - Racine de 3 supp ou égal à x
Voilà donc la fonction est définie sur R+ et là elle n'est privée d'aucune valeur non?
Merci!
Pour la 4) voilà ce que j'ai fait:
Il faut que le dénominateur soit égal à 0, résolvons donc:
x-3=0
x=3
Donc la fonction est défini sur R-3.
Bon?
vous vouliez dire non nul
3 est une « valeur interdite» mais il y a une autre condition puisque vous avez une racine carrée
Pour là 4) attention, il faut également que ce qui ait à l'intérieur de la racine soit positif
donc x2 - 1 > 0
Oui je l'ai déjà fait avant que vous n'écriviez votre réponse...
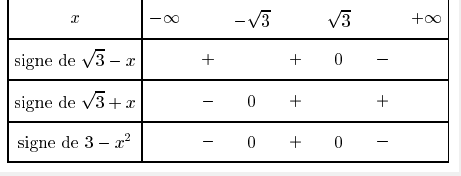
x^2-1 supp ou égal à 0
(x- racine de 1)(x + racinde de 1) supp ou égal à 0
J'ai fait le tableau de signes, je trouve S = ]- infini ; - racine de 1 ] U [ racine de 1 ; + infini[
Donc on dit que la fonction est définie sur R - 3
Mais on pécise qu'elle est positive, mais ce qu'on vient de calculer ici avec le tableau de signes et l'inéquation on en parle pas dans le domaine de def, enfin ca n'en fait pas partie non?
Merci.
Maria.
les conditions sont
la première condition se traduit par et la seconde en refaisant la démarche de l'exercice précédent
donc en prenant les deux conditions
toujours commencer par établir toutes les conditions après les résoudre enfin prendre l'intersection des ensembles solutions
Elle n'est pas définie sur IR \ {3} attention, son domaine de définition est :
Df = ]- ; -1] U [1 ; 3[ U ]3 ; +
; -1] U [1 ; 3[ U ]3 ; + [
[