Inscription / Connexion Nouveau Sujet
Eclipse de soleil
Bonsoir 
J'ai un exercice concernant une eclipse de soleil que je n'arrive pas à résoudre.
Une fois l'énoncé recopié, je vous ferai part de mes brouillons si je puis dire et j'aimerai que l'on me conseille ou que l'on me corrige 
Enoncé:
Une personne observe une éclipse de Soleil.
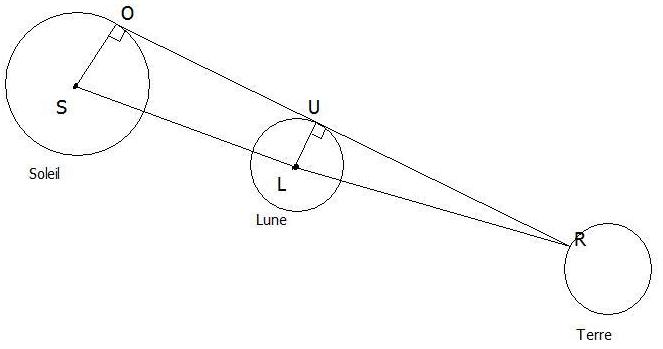
La situation est schématisée par le dessin suivant:
(voir schéma ci dessous)
L'observateur est en R. Les points S (centre du Soleil), L (centre de la Lune) et R sont alignés. On donne:
SO = 695 000 Km (rayon du Soleil) LU = 1 736 Km (rayon de la Lune) RS = 150 millions de Km.
1) Prouver que les droites (OS) et (UL) sont parallèles.
2) Calculer une valeur approchée de la distance RL en km.
Pour le 1), je pensais utiliser la réciproque du théorème de Thalès en faisant:
RS sur RL = RU sur RO mais il me manque des mesures... ?
Pour le 2), théorème de Pythagore?
Merci d'avance pour votre aide 
Pierre-Alexandre.
Oui, puisque (OS)est perpendiculaire a (OR) et (UL) aussi.
Or
Que penses-tu de deux droites perpendiculaires à une même troisième ?
D'accord, merci 
Et pour la question 2), j'utilise le théorème de Pythagore pour trouver la longueur RL?
Pierre-Alexandre.
Oui, on a (OS) perpendiculaire à (RO) et (UL perpendiculaire à (RO). Donc (OS) et ((UL) sont parallèles.
Pour calculer RL, c'est Thalès...
Merci dpi.
J'ai remarqué effectivement que (RU) est tangente au cercle en U mais sans la figure je n'aurais pas fait un triangle rectangle en U mais en L et S.
J'aurais eu aussi 2 droites parallèles et J'aurais pu utiliser Thalès mais C'est faux donc pourquoi?
Voilà ma question...



 ORet UL
ORet UL UL
UL

