Inscription / Connexion Nouveau Sujet
Enigmo 103 : Une balle contre un mur
Bonjour,
voici un petit problème à propos d'un petit jeu tout simple : une personne lance une balle contre le sol, qui rebondit contre le mur, qui revient ensuite dans la main du joueur.
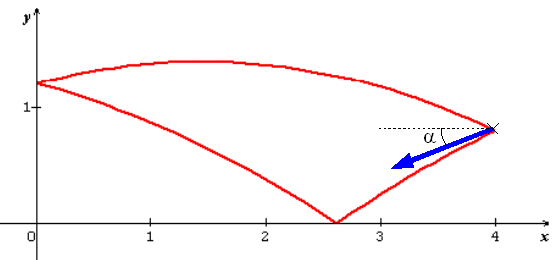
La balle est lancée à une vitesse initiale de 10m/s, en un point situé à 4m du mur et à 80cm du sol en hauteur. La vitesse initiale fait un angle  avec l'horizontale (voir dessin).
avec l'horizontale (voir dessin).
A chaque rebond, la balle repart selon une nouvelle direction : le nouveau vecteur vitesse est obtenu par symétrie de l'ancien par rapport au support où la balle rebondit (en bref, une reflexion classique).
De plus, et c'est important, la vitesse perd 10% de sa valeur à chacun des deux rebonds.
Les trajectoires sont paraboliques, et on prend g=9,81 m/s2 pour l'attraction de l'apesanteur.
Voilà, je crois avoir tout dit.
Question : déterminer la valeur de l'angle  pour que la balle revienne exactement au point initial. La valeur de
pour que la balle revienne exactement au point initial. La valeur de  doit être donnée avec une précision de 0,01°.
doit être donnée avec une précision de 0,01°.
Je rajoute une condition, car je crois bien qu'il existe au moins une autre solution, mais qui fait que la balle va trop haut lors du dernier trajet. Voici cette condition : l'angle  est compris entre 5 et 45°.
est compris entre 5 et 45°.
Question subsidiaire : pourquoi cette photo ?
Bonne recherche ! 

 J'ai très peu de connaissance dans ce domaine, mais : "qui ne tente rien n'a rien".
J'ai très peu de connaissance dans ce domaine, mais : "qui ne tente rien n'a rien".
J'en conclue que l'angle
 31.17.
31.17.
Pour la photo, je crois que c'est un film avec des prisonniers lors de la seconde guerre mondiale, et qu'à se moment là ce personnage (le héros) tente d'éviter d'autres motards nazis. Du moins je le pense. Sinon je réponds que la photo consiste...(quelle colle!)
Merci messieurs et bonne soirée 
 Je ne répondrai pour l'instant qu'à la question subsidiaire, c'est la trajectoire de la balle de baseball que lançait Steve dans son trou, dans "The Great Escape".
Je ne répondrai pour l'instant qu'à la question subsidiaire, c'est la trajectoire de la balle de baseball que lançait Steve dans son trou, dans "The Great Escape".
 coucou
coucou
pour l'énigme je suis incapable d'y répondre par contre la photo c'est Steeve McQueen sur une Triumph, moto utilisée dans le film " La Grande évasion ", il s'est évadé d'un camp en passant au-dessus des barricades en fils barbelés. Une autre photo celle-ci de l'évasion
Désolée pour cette intrusion
Louisa 

 Bonsoir,
Bonsoir,
voici ma proposition :
alpha=26.47 degrés
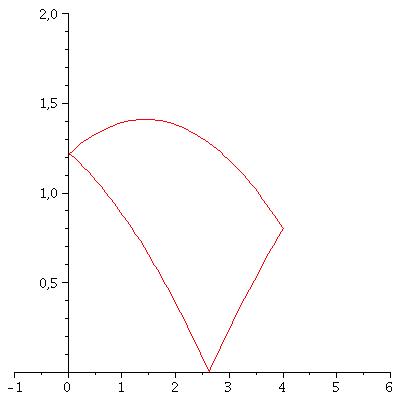
Et voici un petit tracé de la trajectoire
Merci pour l'énigme 
1emeu
 Bonsoir Jamo... là tu nous soignes !
Bonsoir Jamo... là tu nous soignes !
Hors de question de communiquer une valeur exacte de l'angle... j'ai écrit les équations paramétriques des paraboles... la calculatrice s'est chargé du reste !
sauf erreur ou omission, l'angle arrondi à 2 décimales devrait valoir 
 26,19 °
26,19 °
il semblerait bien qu'une autre valeur existe, mais celle-ci me semble la seule dans l'intervalle indiqué.
cordialement
MM
 un petit complément d'information au sujet de ce problème...
un petit complément d'information au sujet de ce problème...
pour toucher le sol en premier, et pas le mur, on doit avoir 
 0,22°
0,22°
pour qu'après le premier rebond, la balle touche le mur avant de retoucher le sol, il faut 
 77,28°
77,28°
pour 
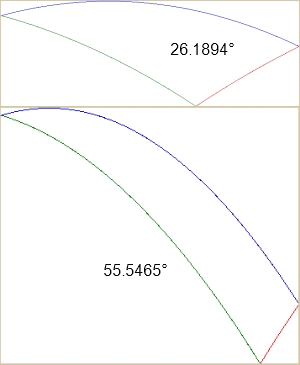
 26,19° (la solution présumée !) la balle touche le sol à environ 2,61 m du pied du mur et rebondit ensuite sur le mur à environ 1,21 m de haut.
26,19° (la solution présumée !) la balle touche le sol à environ 2,61 m du pied du mur et rebondit ensuite sur le mur à environ 1,21 m de haut.
une autre solution est possible en dehors des limites fixées par Jamo : 55,55° (attention : ceci n'est pas ma réponse à l'énigme  ) pour laquelle la balle touche le sol à 3,48 m du mur et rebondit sur le mur à 3,34 m de haut.
) pour laquelle la balle touche le sol à 3,48 m du mur et rebondit sur le mur à 3,34 m de haut.
le tout bien sûr sauf erreur ou omission de ma part...
MM
 Bonsoir
Bonsoir
énigme vraiment diabolique surtout au niveau du calcul !!
je trouve 
 26.19°
26.19°
merci pour l'énigme
 Je trouve un angle de 26,19° à 0,01° près.
Je trouve un angle de 26,19° à 0,01° près.
Dans le film "La grande Evasion", Steve Mac Queen joue à la baballe dans sa cellule pour passer le temps (2 rebonds, comme ici). Il aurait pu prendre le temps de faire des calculs !!!

Sauf erreur, l'angle est de 36,08°
La photo est celle de Steve McQueen dans le film "La grande évasion" et l'énigme est inspirée du lancer de balle de base ball auquel il s'exerce dans son cachot...
Merci pour cette énigme.
 Bonjour
Bonjour
l'unique solution respectant la contrainte [5 ; 45] arrondie à 0.01 est
26.19°
Je me permets d'indiquer ci dessous les deux solutions hors contrainte, avec les trajectoires suivies.
 Après des calculs assez longs, qui sont assez fastidieux à mettre sur le site, je trouve une solution avec l'angle de départ de la balle alpha= 26°,19
Après des calculs assez longs, qui sont assez fastidieux à mettre sur le site, je trouve une solution avec l'angle de départ de la balle alpha= 26°,19
On pourrait envisager une deuxième solution en lançant directement la balle vers le mur et qui reviendrait au point de départ après un rebond sur le sol vers le lanceur.
La trajectoire serait légèrement différente puisque l'ordre des pertes de vitesse serait en sens inverse.
Il est bien évident, car cela n'a pas été mentionné dans l'énoncé, que le frottement dans l'air est négligé. il s'agit donc d'une trajectoire idéale.
La photo de Steve MacQueen est extraite du film "La Grande Evasion" où le héros pourchassé par les allemands lors de la 2e guerre mondiale se lance avec sa moto au-dessus d'une barrière de barbelés grâce à l'accélération qu'il produit.
Bonsoir
 La question subsidiaire (avec ou sans poisson)
La question subsidiaire (avec ou sans poisson)
Steeve Mac Queen dans sa cellule passe sa vie à lancer la balle contre le mur pour qu'elle revienne dans sa main.
Ce qui prouve que le cerveau humain intègre tous les calculs que ne manqueront pas de faire les gentils membres.
1/ Sans la pesanteur le problème est impossible (au billard il faudrait une bande de plus)
2/ je propose 11°31
 Si je ne me trompe pas, la réponse est 25.85° à 0.01 près. J'ai trouvé une seconde solution effectivement en dehors de l'intervalle demandé de l'ordre de 64.15°
Si je ne me trompe pas, la réponse est 25.85° à 0.01 près. J'ai trouvé une seconde solution effectivement en dehors de l'intervalle demandé de l'ordre de 64.15°
Merci pour ces énigmes.
 Bonjour Jamo,
Bonjour Jamo,
Je trouve 26,18° pour Alpha par défaut.
Qs: Dans la grande évasion, "le roi du frigo" (Steve Mac Queen) joue à la balle au mur en prison.

Merci pour cette énigne.
 Bonjour
Bonjour
---------Reponse proposee----------
Je trouve un angle de 26,19° vers le bas.
---------Methode employee---------
Il n'y a pas de difficulte majeure a exprimer, en fonction de alpha, le lieu des rebonds, les vitesses et angles d arrivee ainsi que les durees des trajets; ensuite, les angles de rebond s expriment par symetrie de ceux d arrivee et les vitesses de rebond sont diminuees de 10%
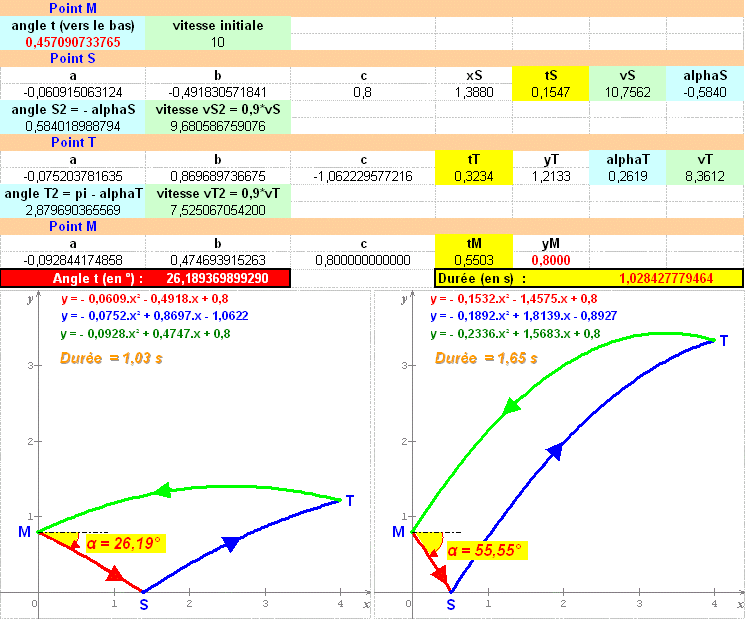
En utilisant Excel, la seule difficulte est d eviter les risques d erreur de calcul (voir image jointe)
Sans garantie pour la valeur de l angle alpha initial, bien que la figure proposee semble etre la symetrique de celle de l enonce...
--------Complement d etude-----------
On peut trouver egalement l autre valeur de alpha repondant a l enonce : je trouve 55,55° vers le haut;
il est aussi interessant de determiner la duree du cycle : sauf erreur, environ 1 s.
Une autre recherche est d envisager un premier rebond sur le mur, le second au sol, puis de revenir dans la main...
Rudy
 Bonjour,
Bonjour,
L'angle  vaut environ 26,19°.
vaut environ 26,19°.
Merci pour le graphique, qui correspond tout-à-fait au mien ! 
Et merci pour l'Enigmo. 
 J'ai essayé au hasard avec quelques valeurs... et 26,19° semble bien convenir. L'énigme est-elle faisable élégamment, c'est-à-dire avec juste un crayon et du papier (moins d'une rame) ?
J'ai essayé au hasard avec quelques valeurs... et 26,19° semble bien convenir. L'énigme est-elle faisable élégamment, c'est-à-dire avec juste un crayon et du papier (moins d'une rame) ?
Merci pour cette énigme.
 J'avais oublié la question subsidiaire : il me semble que dans "La grande évasion" Steve McQueen s'amuse justement à lancer une balle contre le mur et à la rattraper.
J'avais oublié la question subsidiaire : il me semble que dans "La grande évasion" Steve McQueen s'amuse justement à lancer une balle contre le mur et à la rattraper.
 Après calcul, j'ai trouvé
Après calcul, j'ai trouvé  = 16.85°
= 16.85°
Pour la question subsidiaire, je crois que cette image est tirée du film où le héro s'amusait à envoyer la balle contre le mur pour passer le temps à chaque fois qu'il allait au trou (mais je ne me souviens plus du nom de ce film)
 Bonjour Jamo,
Bonjour Jamo,
j'ai trouvé cette enigme difficile, de la physique avec un angle alpha, comme l'histoire de la tasse (oui l'enigmo de la tasse m'a frustré!!! )...
Allez, je tente quand meme ma chance je propose un angle 
 26.18936989° soit à l'arrondi
26.18936989° soit à l'arrondi  =26.19°.
=26.19°.
Pour la méthode j'ai calculer les paraboles, mais cela me parait impossible à faire sans un logiciel de calcul come maple par exemple...
En tout cas merci pour cette enigme très interessante (comme toutes d'ailleur!!!)...
 Bonjour Jamo,
Bonjour Jamo,
Après environ 240 erreurs de calculs, je propose la réponse suivante:
L'angle vaut \alpha = 26,19 ° vers le bas, ou bien -0,45709 radians en orientant l'angle.
En espérant que ce soit juste  :)
:)
 Bonsoir Jamo,
Bonsoir Jamo,
L'énoncé ne précisant pas la taille de la balle, je me suis autorisé à la modéliser par un point.
Deux angles répondent aux conditions de l'énoncé: 26,19° et 55,55°.
La condition supplémentaire donne pour solution unique =26,19°.
On en déduit que la cellule du Capitaine Hilts "The Cooler King" a une hauteur comprise entre 140,68 cm et 343,24 cm.
Clôture de l'énigme
la bonne réponse était : 26,19°. Il existe en effet une autre solution pour 55,55°.
Pas besoin de grands outils de calculs pour trouver la solution. Il suffisait d'établir les équations des trajectoires en fonction des conditions initiales, puis, une fois ce travail un peu lourd effectué, un petit tour sur un tableur permettait d'obtenir facilement la solution.
Pour la question subsidiaire, la photo était tirée du film "La Grande Evasion", où le héros principal, joué par Steve Mac Queen, passe son temps à jouer de la sorte avec sa balle de base-ball contre le mur quand il est mis "au trou".
Cette scène a même été reprise dans le film d'animation "Chicken Run" qui est une parodie de "La Grande Evasion" dans une basse-cour ! 
Félicitations à ceux qui ont trouvé, je crois que cette énigme a fait le "ménage" dans le classement du mois où il restait beaucoup de monde avec le maximum de points pour l'instant.
Mais rassurez-vous, rien n'est perdu, la dernière énigme du mois va encore faire du ménage de manière encore plus sévère ...
Nombre de participations : 0
Temps de réponse moyen : 127:21:57.


