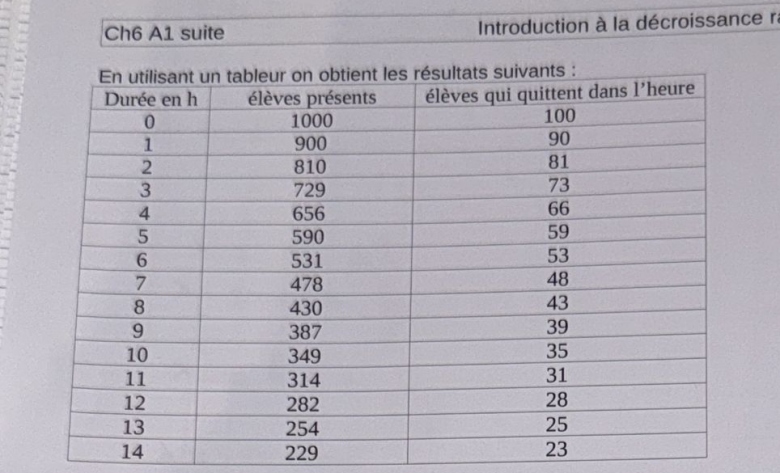
1)rappelez la définition de la dérivée

c'est la lim , quand t tend vers 0 de

(N+t)-N(t))/t

2)en déduire le lien entre et V_disp(t): le nombre de disparition d'élèves par unité de durée  (seconde généralement)

3)Pour un intervalle dt, écrire la relation V_disp(t) et N(t),p et t

en déduire une relation entre N(t) et

vérifier que N(t)=Ae^{-t}+B

pouvez vous m'aider à partir de la 2?

je dirais que V_disp(t):le nombre de disparition d'élèves par seconde?

Bonjour,

Pour 2, OK à un détail près : prendre en compte le sens du mot "disparition".

Pour 3) Il faut traduire mathématiquement p :

merci beaucoup

-V_disp(t)
c'est une fonction décroissante

p=

?

OK pour la correction de signe, mais ce n'est pas lié à "fonction décroissante", mais au sens du mot disparition qui donne donc le nombre d'élèves qui sortent, opposé à la variation du nombre d'élèves restant.
Pour p, il manque la traduction de "sur chaque intervalle de temps Δt."

J'ai calculé un taux d'évolution entre deux périodes t et t+

je trouve une baisse de 10/100 chaque année

je suis arrivé à

j'ai compris la correction mais je voudrais terminer

Vérifier que N(t)=Ae^{-t}+Best solution de cette équation
j'ai dérivé : N'(t)=-Ae^(-t)

déterminer
quel est le nombre final d'élèves pour t=+?
0
en déduire la valeur de B
quel est le nombre initial d'élèves?
en déduire la valeur de A

je trouve A=1000

pouvez vous m'aider pour les questions sans réponse?

Bonjour,

Vous connaissez N(t) et N'(t), il suffit donc de reporter dans votre équation pour trouver B et λ.
(Vous êtes sûr de la présence de B ?)
B=0 d'après l'équation ce qui implique que le nombre final est nul et pas l'inverse. Vous êtes sûr de votre texte ?

oui il y a bien la question en déduire la valeur de B

=p/t

je ne vois pas comment trouber la valeur de

Remarque : il faudrait qu'un mathématicien de passe par là, parce qu'on a n'a pas une équation différentielle, mais une "équation différentielle approximative" .
Faut-il trouver la "vraie" valeur de λ ?

Bonjour,

Je ferais ceci :

dN(t)/dt = -0,1 * N(t)  (1) est l'équation différentielle.
et N(0) = 1000 (tiré du tableau est une condition initiale)   (2)

Avec  N(t)=Ae^{-L*t}+B   comme solution supposée.
avec (2) --> 1000 = A + B  (3)

dN(t)/dt = -A.L.e^{-L*t}
Remis dans (1) -->

-A.L.e^{-L*t} = -0,1 * (A.e^{-L*t}+B )   (4)
Cette relation (4) doit être respectée pour tout t, donc aussi pour t --> +oo
Ceci impose alors : 0 = -0,1 * (0 + B), soit donc B = 0
et avec (3) --> A = 1000

La relation (4) devient donc : -1000.L.e^{-L*t} = -0,1 * 1000.e^{-L*t}  
L.e^(-L*t) = 100.e^(-L*t)
… qui doit aussi être respectée en t = 0 et donc L*1 = 100 *1--> L = 100

Donc N(t) = 1000.e^(-100t) est solution du problème.

Bonjour,

Distraction en fin de rédaction de ma réponse, je recommence :

Bonjour,

Je ferais ceci :

dN(t)/dt = -0,1 * N(t)  (1) est l'équation différentielle.
et N(0) = 1000 (tiré du tableau est une condition initiale)   (2)

Avec  N(t)=Ae^{-L*t}+B   comme solution.
avec (2) --> 1000 = A + B  (3)

dN(t)/dt = -A.L.e^{-L*t}
Remis dans (1) -->

-A.L.e^{-L*t} = -0,1 * (A.e^{-L*t}+B )   (4)
Cette relation (4) doit être respectée pour tout t, donc aussi pour t --> +oo
Ceci impose alors : 0 = -0,1 * (0 + B), soit donc B = 0
et avec (3) --> A = 1000

La relation (4) devient donc : -1000.L.e^{-L*t} = -0,1 * 1000.e^{-L*t}  
L.e^(-L*t) = 0,1.e^(-L*t)
… qui doit aussi être respectée en t = 0 et donc L*1 = 0,1 --> L = 0,1

Donc N(t) = 1000.e^(-0,1.t) est solution du problème.