il n'y a que 2 issues (rouge ou violet) non équiprobables (3/4 et 1/4 comme tu l'as dit), c'est du simple bon sens.

Que penses-tu de ma réponse du 2) stp ?

oui c'est bon (les 4 secteurs sont équiprobables mais les alternatives rouge/violet non) ça ne contredit rien du tout.

Merci Glapion.
Donc en fait tout ce que je dis est correct ?
Pourtant il semble y avoir une ambiguïté qui me gène et je ne comprends pas d'où cela vient.

je ne vois pas d'ambiguïté ni de contradictions. les probabilités sont proportionnelles à la surface des secteurs. si les secteurs n'ont pas la même surface, ils ne sont pas équiprobables.

Donc pour toi, 1) et 2) se complètent et ne se contredisent pas ?

pas le bon forum ...

Bonsoir,
je dirais que l'on fait tourner la roue d'un angle tel que (mod 2) suive une loi uniforme sur [0 ; 2[.

Ensuite la probabilité pour que la flèche pointe sur un secteur donné est proportionnelle à l'angle de ce secteur.

En gros on est bien dans une situation d'équiprobabilité.

Mais, comme on ne s'intéresse qu'a la couleur du secteur, on peut réduire le modèle en ne considérant que deux événements élémentaires (issues ?) {rouge} et {violet} de probabilités respectives 3/4 et 1/4.

Il faut remarquer que les valeurs 3/4 et 1/4 proviennent de l'équiprobabilité des angles.

Pour des élèves, si, comme je le pense,  ils ne connaissent pas les lois continues, on peut dire qu'il y a un clou tous les degrés, et que la roue s'arrête forcément entre deux clous.  Et que l'on admet que toutes les positions d'arrêt possible sont équiprobables.

Puis on simplifie le modèle de la même façon.


Une dernière remarque : je faisais ça avec mes élèves, mais je ne suis plus vraiment au courant des programmes .

Salut carpediem.
Je pense que c'est le bon forum.
Matheuux pose une question sur la présentation des probas, je n'ai pas l'impression qu'il ait la moindre difficulté pour comprendre que les probas demandées sont 3/4 et 1/4.

C'est la justification qui m interesse et ce que je dois dire aux eleves.. car je ne sais pas quoi leur faire ecrire comme correction

La justification est dans l'équiprobabilité des angles de rotations (modulo un tour).
Si on n'a pas cette équiprobabilité, on ne peut rien dire.
Par exemple, si je fais tourner dans le vide la roue avant de mon vélo, elle s'arrête toujours la valve en bas. Il n'y a pas de hasard.

Je ne sais pas à quel niveau tu enseignes, mais je te recommande le modèle discret, du genre on tire au hasard, et avec équiprobabilité, un angle mesurant un nombre entier de degré entre 1° et 360°.
Le résultat est « rouge » entre 1° et 270°, « violet » entre 271° et 360°.
Donc P(rouge)=3/4 et P(violet)=1/4.

Ensuite on prend un modèle plus simple, et sans équiprobabilité.

Maintenant, je ne connaît pas les derniers caprices des IPR sur la question.

Merci verdurin pour ta reponse.
Et toi, que dirais-tu de ce que j ai ecrit dans mon msg initial ?

Bonjour Matheuux
il est écrit "La roue équilibrée ..."
pour moi, je rejoins verdurin, en disant qu'il y a équiprobabilité

Que j'en pense beaucoup de mal.
Et que le mal que j'en pense provient de l'énoncé, je pense qu'on devrait pendre ses auteurs haut et court, au moins métaphoriquement.

Je crois que la réponse attendue à la première question est qu'il y a deux issues.
Ce qui est particulièrement idiot, car, après il n'y a aucune méthode raisonnable permettant de calculer leurs probabilités, sauf à considérer qu'il n'y a pas que deux issues.

Sinon, il me semble avoir étalé mon opinion sur ce que peut-être une solution :
l'équiprobabilité sur les angles entraîne l'absence d'équiprobabilité sur les couleurs.
Et on a la possibilité de prendre un modèle sans équiprobabilité en se limitant aux couleurs.

oui, équiprobabilité sur les angles (je n'avais pas précisé dans mon message précédent)

Je trouve cela compliqué de donner une reponse claire aux eleves...

a) 2 issues "obtenir rouge " et "obtenir violet"
b)3/4 et 1/4

Ce qui me gene c est qu il n y a equiprobabilite sur les couleurs mais qu il y a equiprobabilite des secteurs lorsque je partage la roue en 4 secteurs identiques.

Salut malou

Parce qu on pourrait dire aussi qu on applique la formule "nombre de cas favorable sur nombre de cas possible" - 270° / 360° = 3 / 4 alors qu il n y a pas equiprobabilite...

à quel niveau cet exo était posé ? (habituellement ce type d'énoncé est complété par une phrase du genre "la proba....est proportionnelle au secteur" non ?

Non pas sur cet exo.
Je t ai copie ce qui etait ecrit.

Quelle difference y a t il entre secteurs identiques et la proba... est proportionnel au secteur ?

Imaginons par exemple j ai une roue partage en 8 secteurs identiques : le raisonnement est-il le meme ? Ces 2 informations (secteurs identiques et proportionalite) apportent elles les memes infos que pour la roue precedente (90° ; 270°) ?

?

moi je n'ai pas compris ce qui vous tracasse ?
j'aurais répondu aussi :
a) 2 issues "obtenir rouge " et "obtenir violet"
b)3/4 et 1/4

quoi d'autre ?

Salut Glapion.
Comment justifies-tu la réponse b) ?

ben si un des angle est 90° et l'autre 270° et que les probabilités sont proportionnelles aux surfaces, ça donne 3/4 ; 1/4, je ne vois pas vraiment ce que l'on pourrait dire d'autre sur un problème aussi simple

moi j'ai pensé que c'était sous entendu l'équiprobabilité des deux issues.
(puisque la question est "2) Détermine la probabilité de chacune de ces issues. ")
donc en bon français, "elles sont équiprobable, si elles sont égales"
et donc la réponse est non.

mais je vois qu'on peut chinoiser à l'infini sur un truc comme ça, j'aurais jamais imaginé ça .

Pour continuer à pinailler.

Je ne sais pas vraiment ce qu'est une « issue ».
Disons que je prendrais ça dans le sens :
on a un espace probabilisé  
une issue est un élément de .

Ici est le cercle, la tribu des boréliens et P est proportionnel à la mesure de Lebesgue.

Une issue est un angle, et comme l'aire d'un secteur est proportionnelle à la longueur de l'arc, la probabilité d'un secteur est effectivement proportionnelle à son aire.

Comme c'est  hors programme dans le secondaire, on peut discrétiser le problème en disant que l'on divise la roue en un certain nombre de secteurs isométriques qui sont équiprobables, par exemple avec des clous qui interdisent les cas ambigus sur la limite rouge - violet.
Une issue est alors un de ces secteurs et les issues sont équiprobables.

Ensuite on s'intéresse à deux événements : « la flèche indique rouge »,  « la flèche indique violet » et on calcule leurs probabilités.


Mais il est très clair pour moi que la réponse attendue est celle qu'a donnée Glapion.
Le seul problème est qu'elle n'a aucun sens mathématique, même si elle est presque évidente intuitivement.

La question que me pose cet exercice est :
doit-on faire des maths en cours de math, ou se limiter à de vagues intuitions ?

L'auteur de l'énoncé a manifestement tranché pour les vagues intuitions.

Et je suis vraiment désolé de voir que, même dans le forum  espace profs,  se limiter à de vagues intuitions semble suffisant.

ouais ... mais bon ...

se donner U = {bleu, rouge} avec P(B) = 1/4 et P(R) = 3/4 et interpréter cela avec une roue et des secteurs d'1/4 et de 3/4 peut sembler convenable ... quand on introduit les proba

de même que quand on introduit les intégrales on interprète leur résultat par des aires ...

il faut distinguer :

introduire une notion à quelqu'un qui n'en connait rien et on peut "être "un peu" approximatif" dans un premier temps puis formaliser tout cela avec rigueur ultérieurement dans la poursuite d'étude

et

introduire une notion par quelqu'un qui en connait "beaucoup plus" et sait toutes les éventuelles imperfections du biais utilisé pour introduire ces notions ...

D'accord.
On peut dire :
on s'intéresse à deux événements et leurs probabilités respectives sont 3/4 et 1/4 intuitivement.

Mais introduire le vocable « issue » me semble être une erreur.

Et la question 1) devrait plutôt être :
une roue est  colorée exclusivement en rouge ou en violet, combien y a t-il de couleurs utilisées ?

C'est évidement moins prétentieux, on voit directement que c'est du niveau CP, mais c'est plus précis.

En fait je reproche surtout à ce genre d'exercices d'avoir des prétentions à une rigueur qu'ils n'ont pas.
On emploie de grands mots vides de sens, et on croit que c'est une science.

Et je dirais que c'est le malheur de l'enseignement, dans le secondaire, des probas et des stats.

Bonsoir Verdurin, pourquoi ta formulation de la question 1) est-elle plus precise ?
Merci.

Issue est une reponse, un resultat que l on obtient suite a une experience aleatoire.
Ici, rouge et violet.
Cependant les probas que l on cherche ne sont, pour moi, pas des probas d issues (ce qui n a pas de sens me smble t il) mais des probas d evenements elementaires "Obtenir rouge / violet".

J'ai beaucoup de mal à croire que « rouge » soit un événement élémentaire.
Si c'est le cas il est impossible de calculer sa probabilité.

Les issues (l'univers) sont les positions relatives de la roue et de la flèche.
Ensuite on considère des événements, parties de l'univers.
Enfin on peut considérer une sous-tribu réduite aux parties de {rouge, violet} munie d'une probabilité qui n'est pas uniforme.

Mais, je crois, il est important que les élèves comprennent que l'on est pari d'un univers grand et que l'on le restreint à ce qui nous intéresse ce qui fait un univers petit.

En ce sens il est essentiel de préciser que la probabilité d'un secteur est proportionnelle à son angle au centre (ou à son aire, ou à la longueur de l'arc)

Pour prendre un exemple plus simple : je lance trois fois une pièce équilibré ou non et je compte le nombre de « pile ».
On peut bien sur dire qu'il y a quatre issues : 0 ; 1 ; 2 ; 3.
Mais pour calculer les probabilités, on est obligé de considéré qu'il y en a huit.

Je comprends : tous les triplets avec Pile et face conduisent à 8 resultats.
Je comprends qu il y a 4 issues mais ne comprends pas ce qui s opposent.
Du coup, la resolution de cet exercice pour des 4emes me parait imbuvable : je ne sais pas comment faire des probas proprement à ce niveau avec de tels exercices...

Pour préciser encore, voici deux images ( je n'ai mis que le rouge).

Il s'agit manifestement de deux issues distinctes.

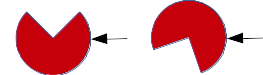
Je dois bien dire qu'il y a très longtemps que je n'ai pas eu de quatrième. . .

Je crois qu'il faut fixer le vocabulaire.

Une issue est un résultat possible et, en quatrième, je dirais qu'une issue un angle mesuré par un nombre entier de degré entre 1 et 360. Bien sur on peut aussi se limiter à quatre secteurs de 90° équiprobables, mais je crois qu'il vaut mieux donner beaucoup de secteurs, pour favoriser l'intuition des probabilités continues
Dont j'éviterai soigneusement de parler.

Ensuite, on affirme que « roue équilibrée » signifie que ces secteurs sont équiprobables.

Puis on a deux événements qui nous intéressent « rouge », « violet ».

Comme on a 270 secteurs rouges sur 360 secteurs possibles P(rouge)=3/4.

En résumé, on part d'une situation d'équiprobabilité ( le hasard ).
Puis on calcule des probabilités.

Ceci étant dit, c'est mon avis, et, pour moi, il est évident que j'ai raison.
C'est moins évident pour d'autres.

Qu'est-ce que vous aimez compliquer les choses ! :
les deux issues ici c'est la flèche tombe sur rouge ou violet (avec des probabilités 3/4 ; 1/4)
Avec des quatrièmes, il faut savoir expliquer les choses simplement.

Bonsoir Glapion.

On pinaille, on se complique la vie mais en tout cas, personne ne voit les choses de la même manière et personne ne semble avoir les mêmes interprétations d'un exercice de 4ème...
Cet exercice aura au moins eu la vocation de nous permettre un véritable échange.