Inscription / Connexion Nouveau Sujet
etude d'une fonction et tracé de sa courbe représentative
Bonjour je suis sur cette exercice, je sollicite votre aide merci d'avance
Soit f la fonction définie sur ]0,+∞[ par f(x)= (1/2)(ln(x))² + ex - e
On note Cf la courbe représentative de f dans le plan raporté à un repére orthogonal (4cm en abscisse et 2cm en ordonnée)
1) Verifier que, pour tout x de ]0,+∞[, f'(x)=g(x)
2) Determiner les limites de f en 0 et en +∞
3) Dresser le tableau de variation de f
4) Determiner une équation de la tangente T à Cf, en son point I d'abscisse 1 , Preciser la position de Cf par rapport à T.
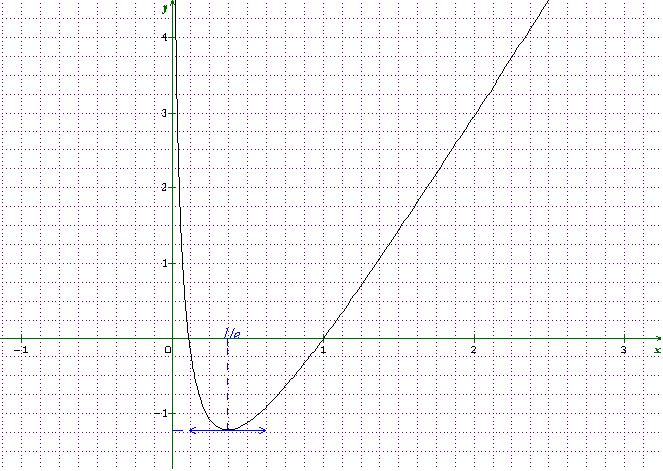
5) Tracer T et Cf
q1) je ne compren pas
q2) lim de (1/2)(ln(x))² lorsque x tend vers 0 = +∞
lim de ex-e lorsque x tend vers 0 =-∞
c'est une forme indeterminé mais apré je ne sait pas quoi faire( factoriser?)
j'ai oublier g(x)= (lnx)/(x) +e
je ne sait pas comment on dérive (lnx)²
la formule la c'est u^n
on a : n=2.u(x).u'(x) = 2.lnx. (1/x) = 2 (lnx/x) ,(1/2).2 . (lnx)/(x)+e= (lnx)/(x) + e = g(x)
comment calculer la limites d'une fonction indeterminé
bonjour, quelqun peut m'aider a calculer cette limite, sachant qu'on a une forme indeterminé, svp merci
bonjour,
question 1)
Pour dériver f, il faut utiliser la formule (u²)'=2u'u.
En particulier, si on pose u(x)=ln x et u'(x)=1/x, alors ((ln x)2)'=2 (1/x)
(1/x) ln x=(2ln x)/x.
ln x=(2ln x)/x.
La dérivée de f est donc bien f'(x)=(ln x)/x+e.
question 2)
La limite en 0 ne pose pas de problème : elle vaut + et il n'y a pas de forme indéterminée.
et il n'y a pas de forme indéterminée.
Par contre, pour la liite en + , il y a bien une forme indéterminée.
, il y a bien une forme indéterminée.
Pour lever l'indétermination, il faut factoriser par x...
bonjour, pour le tableau de variations de f(x)=1/2(lnx)²+ex-e ,j'ai trouver f(x) s'annule pour x = e.(1/e) , mais aprés je ne sait pas comment placer le tableau.
quelq'un peut m'aider svp c'est urgent merci
Bonjour,
Pour le tableau de variation de f, il ne sert à rien de chercher pour quelles valeurs de x la fonction f s'annule... D'ailleurs elle s'annule effectivement pour x=e.(1/e), c'est-à-dire, plus simplement, pour x=1. (mais ce n'est pas la seule valeur)
Par contre, il faut déterminer le signe de f'(x).
Tu as du démontrer que f'(x)=(lnx)/x+e. Cette dérivée s'annule pour x=1/e. Il faut que tu démontres que :
sur l'intervalle ]0;1/e[, f'(x)<0, donc f est décroissante sur cet intervalle
sur l'intervalle ]1/e; + [, f'(x)>0 donc f est croissante sur cet intervalle.
[, f'(x)>0 donc f est croissante sur cet intervalle.
À toi ...
sur l'intervalle ]0;1/e[, f'(x)<0, donc f est décroissante sur cet intervalle
moi je voit sur le graphique que f est quand meme croissante f décroit a partir de e
toutes mes excuses je regardait le mauvais graphique
mais je ne voit pas comment on peut démontrer a part dire que l'on peut voir graphiquement
mais ici c'est pas en ]0;1/e[, que f'(x)<0 on voit que c'est apré 0 a peu prés x=0.2 et f'(x)<0
nn c'est bon j'ai rien dit autant pour moi
On me demande de trouver l'équation de la tangente T en I d'abscisse 1. je sais que l'équation d'une tangente est y = f'(a)(x-a)+f(a) or a=1.
f'(1)=e ; f(1)=ex-e , donc on a y= e+(x-1)+ex-e ; y= ex-e + ex-e
non y= e+(x-1)=ex-e
et f(1)=0
Tangente T au point I d'abscisse 1 :
On a : f(1)=0 et f'(1)=e
Donc l'équation de la tangente T est y-0=e(x-1)
ou encore : y=e(x-1) ou encore y=ex-e.
on me demande de démontrer que l'équation f(x)=0 admer une seule solution notée α dans ]0,1/e[
je doit resoudre 1/2(lnx)²+ex-e=0 c'est bien sa?
Non, tu dois démontrer qu'il existe une solution. On ne te demande pas combien elle vaut car c'est impossible à savoir de façon exacte...
Il faut utiliser simplement le théorème des valeurs intermédiaires.
on étudie en ]0,1/e] la fonction , f'(x)=(lnx)/(x)+e f'(x) s'annule pour x=1/e donc entre 0 et 1/e f'(x) est négatif
et f(x) est décroissante
Non, la dérivée ne sert à rien ici :
->f est décroissante sur l'intervalle ]0;1/e]
->la limite en 0 de f est +
->f(1/e) est négatif
->f est dérivable sur ]0;1/e]
Donc ...l'équation f(x)=0 a une solution unique dans l'intervalle ]0;1/e].
pour trouver une aproximation de alpha il faut faire le tableau avec la calculatrice???
quelqun peut m'aider svp