Inscription / Connexion Nouveau Sujet
Exercice intégrales
Bonjour, j'ai un devoir maison à rendre pour le mercredi 8 Avril, et je suis complètement bloqué dès le début...
Voilà le sujet:
http://www.***.jpg lafol > lien supprimé, fais l'effort de recopier ton énoncé sur le forum, AnthonyduVar, si tu veux de l'aide
Merci d'avance 
Ca risque d'être incompréhensible, il y a des schémas et pas mal de caractères que je ne sais pas ajouter ^^
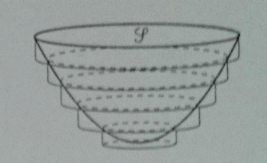
 est le solide engendré par la rotation de l'arc de parabole d'équation z = y² avec -1
est le solide engendré par la rotation de l'arc de parabole d'équation z = y² avec -1 y
y 1 dans un repère orthonormé d'axes oy et oz
1 dans un repère orthonormé d'axes oy et oz
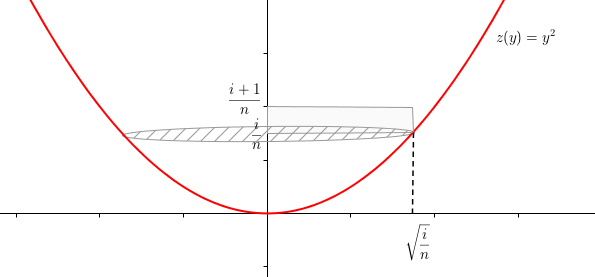
On concoit qu'en encadrant  de + en + finement par un empilage de cylindres, on peut approcher son volume V.
de + en + finement par un empilage de cylindres, on peut approcher son volume V.
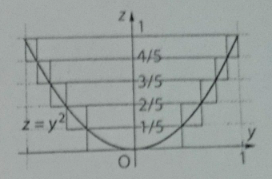
Sur Oz on subdivise [0;1] en n (n 1) sous-intervalles de même longueur
1) sous-intervalles de même longueur
On définit alors n-1 cylindres intérieurs et n cylindres extérieurs
On note Un la somme des volumes des CI (cylindres intérieurs) et Vn celle des extérieurs
1) a Justifiez que pour tout entier n 1, Un=
1, Un= /n² x (1+2+...+(n-1))
/n² x (1+2+...+(n-1))
b) démontrez que pour tout entier n 1, Un =
1, Un =  /2 x n-1/n. En déduire la limite L de la suite Un
/2 x n-1/n. En déduire la limite L de la suite Un
2)a) Prouvez que pour tout entier n 1, Vn= Un+
1, Vn= Un+  /n, puis que Vn converge aussi vers L
/n, puis que Vn converge aussi vers L
b) Déduisez en le volume V du bol. Contient-il plus de 1 litre?
C'est pour la première partie. J'aimerais finir celle-ci en priorité 
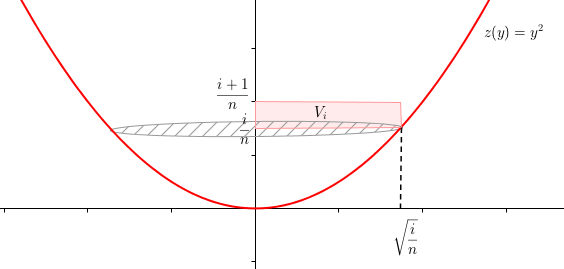
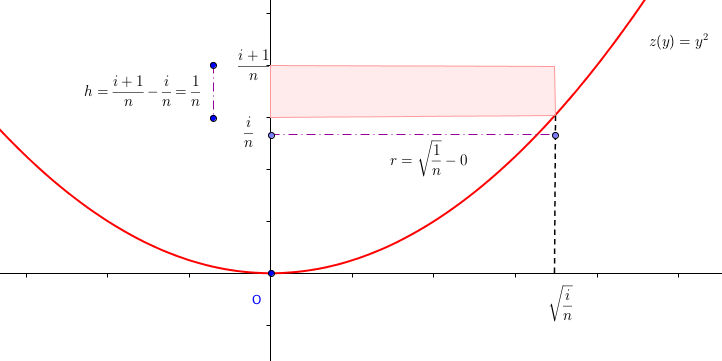
Tu es d'accord que le cylindre intérieur est formé par la bande rosée de la figure ci-dessus et qu'on va faoire tourner autour de l'axe , ok ?
Merci de votre aide mais je ne vois pas comment rédiger la premiere question ... pouvez-vous m'aider ?
Oui volume cylindre pi*r carré * h sa va mais comment on connait r et h ? Et comment obtenir la suite un ?
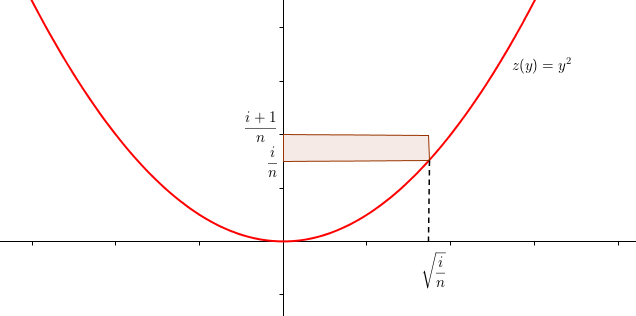
Je comprend d'où vien le i/n et racine 1/n cest parce que cest des cylindres de hauteur h = i/n et comme cest la fonction ycarre on a la racine en abscisse . Cest sa ? sa doit paraitre evident mais sa m'aiderait à mieux comprendre l'exercice ..
v= pi r carre * h
= pi * r carre * ((i+1)/n - i/n )
je comprend pour trouver mais pas pour le rayon cest racine i/n mais pourquoi ?
je comprend pour trouver mais pas pour le rayon cest racine i/n mais pourquoi
Tu as une fonction
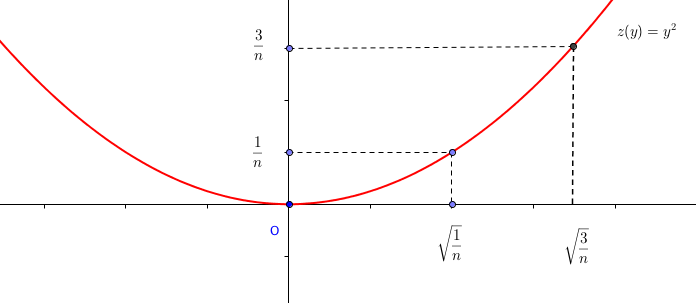
On subdivise l'axe des
Donc sur l'axe des ordonnées on aura
Donc quels sont les antécédents de ces valeurs ?
Je sais pas ce quest latex ...
apres avoir trouve le volume du cylindre, vous disiez devoir faire une somme dans votre ancien message, a quoi cela correspond?
Oui mais je dois rendre ce devoir demain j'ai pas beaucoup avancé depuis je bloque toujours à la première question . Une fois le calcul du volume du cylindre fait, je dois trouver la suite un qui correspond à la somme des volumes des C.i. et Vn
Tu t'y es pris un peu tard pour un devoir aussi difficile (mais fort intéressant au demeurant).
Ta suite est la somme de tous les
de i=1 à i=n-1
En faisant cela et en factorisant, tu retombes sur le résultat demandé.
Pour la question d'après, il t suffit juste de prendre l'expression de la somme des n premiers termes d'une suite arithmétique :
Attention, dans notre résultat on est avec (n-1) termes et non plus n termes.
Aïe, j'ai du t'induire en erreur dans mon post de 17:56. Je t'ai dit :
Notons le volume de ce cylindre, il sera donné par :
J'aurais du te dire :
Notons le volume de ce cylindre, il sera donné par :
Et dans mon message de 18:02, j'ai fait une boulette (pas d'incidence dans le résultat, mais ça peut en avoir dans la compréhension).
J'ai mis :
A présent, il te faut faire :
Il aurait mieux valu mettre :
A présent, il te faut faire :
Je pense avoir trouvé la réponse aux questions 1.a) , b)
Comment faire pour la 2.a) . J'arrive à faire que pour la limite de Vn qui est pi/2 comme Un .