Quand je calcule l'angle sur le schéma je trouve 45*

Bonjour,

une idée intéressante serait de prouver que AM et BP sont perpendiculaires et même mieux que A et P sont symétriques par rapport à la droite BP
(la moitié du boulot est déja faite car les angles en B des triangles rectangles BAP et BMP etc)

oui tout à fait, tu sais ce que tu dois trouver.


Et maintenant prie pour que mathafou vienne t'aider
(c'est le grand spécialiste de ce genre de truc)

ha ha, je ne croyais pas si bien dire !

on peut rajouter quelques points sur la figure, histoire de pouvoir nommer les trucs dont on peut avoir besoin dans la démonstration
comme par exemple des considérations sur le quadrilatère ADIE ou le triangle BIC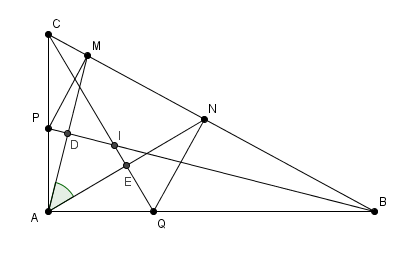

J'ai essayé de montrer que les deux triangles PMB et PAB sont isométriques
On a : l'angle PMB=90° car M est la projection ortogonale de P sur CB
             - L'angle CAB =90° car c'est un triangle rectangle
   puisque (MP) est la bissectrice issue de B sur AC donc les deux angles PBA et PBM sont  
   égaux . D'ou l'angle BPM=BPA
   Or on a : Si deux triangles ont un côté de même longueur compris entre deux angles respectivement égaux, alors ils sont isométriques.Dans ce cas on a BP qui appartient aux deux triangles avec BPM=BPA et PBA=PBM . donc les deux triangles PMB et PAB sont isométriques .

Je ne suis pas sûr de ma réponse , sinon est- ce que ca va servir à démonter quelque chose . j'attend votre confirmation
    

c'est bien ça

et ça va servir à démontrer la première partie de mon plan : prouver que AM perpendiculaire à BP

On a montrer que BPA=BPM
on peut en déduire que (BP)=(BD) est la bissectrice issue du sommet P du triangle APM.
et on vient tout juste de montrer que les deux triangles APB et PMB sont isométriques donc PM=PA ce qui veut dire  que le triangle APM est isocèle en P.
Or, Si un triangle est isocèle alors sa bissectrice est perpendiculaire au coté qui l'oppose.
Alors l'angle APD=ADM= 90°
et puisque D appartient à (BP) et (MA) donc PDM=MDB =90°
D'ou on peut déduire que (AM) est perpendiculaire à (BP)

Est-ce que c'est juste ?

Et je pense que vous vouliez dire qu'il fallait montrer : A et M sont symétriques par rapport à la droite BP

puisque le triangle PAM est est isocèle donc (PD) qui est sa bissectrice est aussi sa médiatrice.
et on avait déjà démontré que PMB et PAB sont isométriques donc leurs hauteurs sont égaux ==> MD=AD
donc puisque MD= AD et que (PD)=(BP) est la médiatrice du triangle APM alors A et M sont symétriques par rapport à la droite (BP)

un peu d'attention, APD n'est pas 90° !! et encore moins ADM avec A, D, M alignés !!

il faudrait rester simple : la bissectrice directement définie comme telle dans l'énoncé est la bissectrice de l'angle B,
donc la bissectrice de cet angle là dans le triangle ABM, tout aussi isocèle
la bissectrice (BD) est donc perpendiculaire au côté opposé (AM) et c'est fini
pas la peine de compliquer inutilement avec le triangle APM

"on démontre de même" pour l'autre (CQ perpendiculaire à AN)

et maintenant je t'ai parlé de quadrilatères etc

posts croisés, ma réponse d'avant était sur le message n-2

il suffit de perpendiculaires, c'est ça uniquement dont on a besoin pour la suite..
la symétrie ne servira plus : c'est en fait la symétrie du triangle isocèle qui a servi à justifier que sa bissectrice est perpendiculaire en général.

on pouvait aussi sans triangles isocèles dire : les triangles isométriques donc PM = PA et BM = BA
P et B sont donc deux points de la médiatrice de AM (propriété caractéristique de la médiatrice), cette médiatrice est donc (BP).

en disant APD=ADM= 90° je voulais dire ADP=PDM  erreur d'inattention désolé

Bonjour,

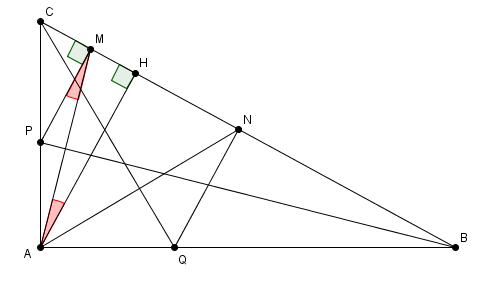
Une voie simple : Si [AH] est la hauteur issue de A, alors AM est bissectrice de l'angle CAH puisque le triangle APM est isocèle par construction.
de même AN est bissectrice de l'angle BAH.Donc l'angle MAN est la moitié de l'angle droit.

Je n'ai pas très bien saisi votre réponse vham , je trouve qu'il ya de la logique , mais j'aimerais bien plus d'explication pour que la réponse soit plus concrète .
Merci en tout cas !

raccourci d'une autre façon de prouver ce qu'on cherche, effectivement astucieuse.

APM n'est pas isocèle par construction
il a été prouvé isocèle via les triangles isométriques précités

il manque la justification exacte de AM bissectrice de CAH (un petit trou facile à combler)

Oui, on a déjà prouvé que APM est isocèle ( non par construction ) reste a démontrer que AM est bissectrice de CAH .

une histoire d'angles et de parallèles ...

Bonjour,

Quand l'énoncé donne P sur la bissectrice de l'angle en B du triangle ABC rectangle en A et donne M projeté de P sur [BC], d'office pour moi le triangle APM est isocèle "par construction" car tout point de la bissectrice est à égale distance des cotés.
Mais bien sûr vous vous pouvez vous obliger à d'autres considérations.
De même vous pouvez estimer qu'il faut écrire que les angles sur la base d'un triangle isocèle sont égaux, et qu'étant donné l'égalité des angles alternes-internes puisque [PM] est parallèle à [AH] et que deux angles égaux à un même troisième etc....
ce doit être ce que mathafou appelle : (un petit trou facile à combler),  que j'ai laissé à la rédaction de roronoalaw pour qu'il voie par lui-même.

puisque AH est la hauteur de ABC issue de , alors AH est perpendiculaire à BC
et puisque PM est perpendiculaire à BC alors (PM)//(AH)
on peut utiliser le théorème de Thalès sur AIMP donc DA/DM=DI/DP=AI/PM
On a déjà démontrer que DA=DM donc AI/PM=1 d'ou AI=PM
puisque AI=PM et que (PM)//(AI) alors PMIA est un parallélogramme
D'ou AM sa diagonale donc l'angle MAI=MAP d'ou MAH= MAC
donc AM est bissectrice de CAH .

Est- ce que c'est juste ?

En disant Parallélogramme je voulais dire losange car on a PM= AI et aussi PM= MI car (MD) est la  médiatrice de PMI   qui passe par le sommet M

ou bien tout simplement car ses diagonales sont perpendiculaires

Sachant que les diagonales d'un losange sont les bissectrices de ses angles.

c'est vrai que en considérant que tous les points de la bissectrice sont à égale distance des côtés on se passe des triangles isométriques de la démonstration d'origine. (j'avais pas tilté)
mais de là à considérer que c'est "par construction" hum
il faut tout de même citer cette propriété pour avoir le droit de l'affirmer !
(donc c'était bien un "trou à combler", sous entendu par roronoalaw)

quand à la suite, roronoalaw vient de nous concocter un truc bien inutilement compliqué aussi
par rapport aux histoires d'angles alternes internes qui tiennent en une demi-ligne (mais encore fallait il combler effectivement ce "trou" et j'attendais aussi que roronoalaw le fasse comme ça suite à ma remarque "une histoire d'angles et de parallèles")

bon là on a tout et il n'y a qu'à mettre au propre en choisissant les morceaux les plus pertinents et simples de la discussion (et explicites).

Donc vous sous entendez que l'histoire du losange etc est fausse ?

non pas fausse mais c'est trop compliqué alors que tout se fait en deux lignes.
(et elles ont été quasiment écrites par vham !)
toute la démonstration en entier de tout l'exo tient en quelques lignes ("en choisissant les morceaux les plus pertinents et simples")

J'aimerais bien que vous m'écrivez la démonstration détaillé de AM est bissectrice de CAH ainsi que AN est bissectrice de l'angle BAH. je me sens un peu perdu à force de trop réfléchir

je vais me contenter de copier-coller ce qu'a écrit vham :

J'ai compris cette partie mais pour montrer que AN est bissectrice de l'angle BAH ??

exactement pareil de l'autre côté (AQN isocèle en Q etc)

généralement quand on a une telle symétrie dans les roles des éléments géométriques on se contente de dire :
"on démontre de même que"
sans répéter les détails exactement copiés-collés de la démonstration d'avant avec juste une substitution de lettres.

Donc si on montre que AN est bissectrice de l'angle BAH et AM est bissectrice de CAH
cela implique que MAN=1/2 * AHM ? si oui je voudrais bien savoir pourquoi , est-ce qu'il s'agit d'une propriété ?

c'est la partie la plus instantanée de la démonstration !!

AM bissectrice de CAH ça veut dire MAH = 1/2 CAH

et de même HAN = 1/2 HAB

on ajoute membre à membre et on tient compte de CAB = 90° (ton AHM n'a rien à faire là)

Je viens de comprendre . Merci infiniment pour votre aide ^^

Bonsoir,

---> mathafou : Merci, je n'ai pas votre patience pour tout bien exposer, et je vais même quelquefois trop vite en étant en erreur,
Vos explications sont toujours très claires et sûres.

salut,
avec geogebra une fois la figure faite,
peut-on obtenir la valeur exacte de l'angle ?
Si oui comment ?

Geogebra fait la dedans des calculs numériques, donc la valeur exacte est une "conjecture" sur Geogebra
il affiche 45° à 10^-15 près ou du même genre.

Bonjour ;

Il y a au moins trois méthodes pour résoudre cet exercice . J'expose la plus simple à mon avis.

Je me rèfère à la figure de mathafou postée à 14h38 .

Considérons le triangle MAN :
MAN = 180° - AMN - ANM .
On a : AMN = 90° - PMA et ANM = 90° - QNA ,
donc : MAN = 180° - 90° + PMA - 90° + QNA = PMA + QNA  : résultat n° 1 .

On a aussi : MAN = 90° - QAN - PAM : résultat n° 2 .

On remarque aussi que M et A sont respectivement les projections orthogonales de P sur [BC) et [BA) , et comme (BP) est la bissectrice de l'angle B , alors on a : PA = PM , donc le triangle PMA est un triangle isocèle en P , donc on a : PMA = PAM : résultat n° 3 .

De même , on remarque que N et A sont respectivement les projections orthogonales de Q sur [CB) et [CA) , et comme (CQ) est la bissectrice de l'angle C , alors on a : QA = QN , donc le triangle QNA est un triangle isocèle en Q , donc on a : QNA = QAN : résultat n° 4.

Conclusion : Les résultats 1 , 2 , 3 et 4 impliquent que :
MAN = 90° - QNA - PMA = 90° - MAN ,
donc : 2 MAN = 90° ,
donc : MAN = 45° .

je connais mal geogebra mais si je fais:
A=(1,2)
B=(1,0)
C=(3,0)

puis dans le module de calcul formel:
Angle[B,A,C]

j'obtiens pi/4

il est probable que dans votre exercice on puisse de cette maniere obtenir la valeur exacte de votre angle

ou faire comme dans mon premier post, on dessine la figure et on demande l'angle.
et on a le plaisir de voir que si on bouge le point A (sur un cercle pour que l'angle reste droit) l'angle MAN reste à 45°

et on est sur que ce soit la valeur exacte ?

Bonsoir ;

Avec Géogebra , on n'est pas sûr que ce soit la valeur exacte .

mathafou l'a déjà dit "Geogebra fait la dedans des calculs numériques, donc la valeur exacte est une conjecture : il affiche 45° à 10-15 près ou du même genre." .

c'est ce qu'il fait dans la fenêtre "Algèbre" et dans la fenêtre graphique pour afficher un angle

par contre alb12 a parlé du module de calcul formel de géogébra
dans lequel par exemple il donne :



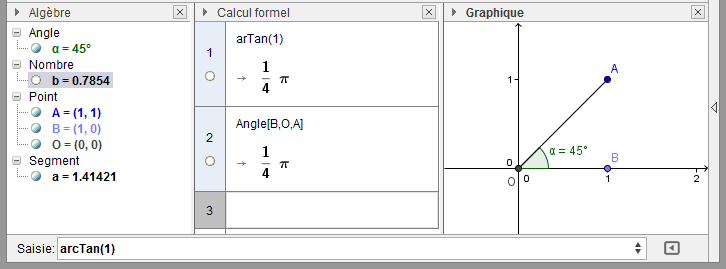
et des valeurs exactes (avec écrit et les racines écrites etc)
ici on voit la différence entre la valeur exacte de arctan(1) dans le calcul formel et la valeur approchée de b=arctan(1) dans la fenêtre algèbre

la question de alb12 est donc : comment lui faire calculer l'angle de notre figure dans le cadre de ce module de calcul formel.
Angle[M,A,N] dans une ligne de calcul formel suffit il ?
faut essayer ...

est-il possible de:
definir A(0,0) B(b,0) et C(0,c) avec 2 curseurs,
faire la figure,
demander Angle[M,A,N] ?

Avec Xcas (la figure n'est pas aussi jolie que celle de geogebrra)

A:=point(0,0);
supposons(b=[5.6,0,10,0.1]); // cocher symb pour un calcul litteral
B:=point(b,0);
supposons(c=[3.3,0,10,0.1]); // idem
C:=point(0,c);
biss1:=bissectrice(B,A,C);
P:=inter_unique(biss1,droite(A,C));
biss2:=bissectrice(C,A,B);
Q:=inter_unique(biss2,droite(A,B));
droite(B,C);
perp1:=perpendiculaire(P,droite(B,C));
perp2:=perpendiculaire(Q,droite(B,C));
M:=inter_unique(perp1,droite(B,C));
N:=inter_unique(perp2,droite(B,C));

angle(A,N,M) // renvoie pi/4
angle(A,M,N) // renvoie -pi/4
angle(M,A,N) // renvoie atan((b+sqrt(b^2+c^2))/c)

avec un curseur a on a la valeur de l'angle exactement mais avec l'affectation actuelle de a
Il semble impossible d'avoir un resultat symbolique.
J'ai essaye ceci:
clic droit sur le curseur>Proprietes>Algebre>cocher symbolique
mais je ne comprends pas à quoi ça sert, en tout cas pas à faire un calcul litteral.
Il faut dire que je connais tres mal geogebra