Inscription / Connexion Nouveau Sujet
Exercice probabilité-suites
Bonjour, j'ai besoin d'aide pour mon DM.
Énoncer: Dans un zoo, l'unique activité d'un manchot est l'utilisation d'un bassin aquatique équipé d'un toboggan et d'un plongeur.
On a observé que si un manchot choisit le toboggan, la probabilité qu'il le reprenne est 0,3.
Si un manchot choisit le plongeoir, la probabilité qu'il le reprenne est 0,8.
Lors du premier passage les deux équipements ont la même probabilité d'être choisis.
Pour tout entier naturel n non nul, on considère les événements:
•Tn: «le manchot utilise le toboggan lors de son n-ième passage.»
•Pn: «le manchot utilise le plongeoir lors de son n-ième passage.»
1.On considère alors la suite (Un)définie pour tout entier naturel n_>1 par:
Un= p(Tn) où p(Tn) est la probabilité de l'évènement Tn.
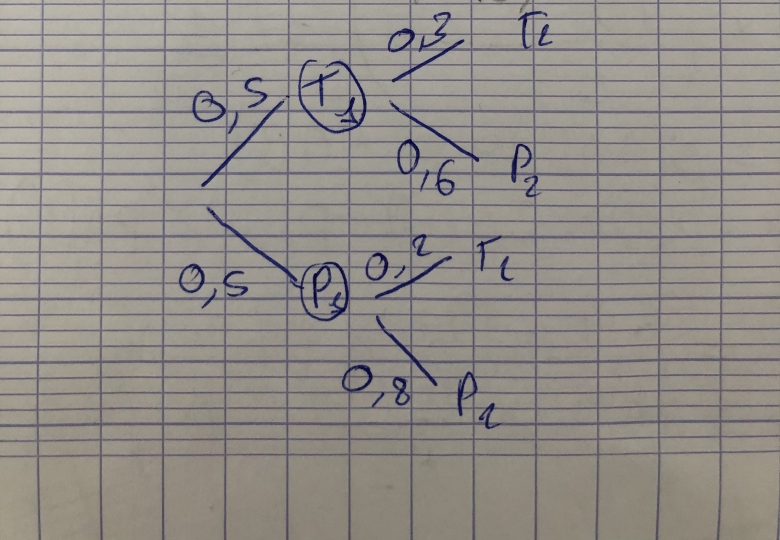
a) Donner les valeurs des probabilités conditionnelles p(T2)sachantT1, p(T2)sachantP1.
b)Montrer que p(T2)=1/4
c)Démontrer que pour tout entier n_>1, Un+1=0,1Un+0,2 (Faire un arbre pondéré)
2.On considère la suite (Vn) définie pour tout entier naturel n_>1 par: Vn=Un-2/9
a)Démontrer que la suite (Vn) est géométrique de raison 1/10.
b)Exprimer Vn en fonction de n. En déduire l'expression de Un en fonction de n.
c)A l'aide la calculatrice, conjecturer la limite de la suite (Un) ( aucune démonstration n'est demandée)
Interpréter ce résultat.
Merci pour votre aide
pour 1b) si tu as des difficultés tu peux faire un petit arbre pondéré au brouillon, pour les 1er et 2ème passage.
1b) non, l'énoncé t'indique que tu dois trouver 1/4, soit 0.25
montre toujours le détail de tes calculs pour je puisse t'aider
0,3*(0,8*0,5)/0,5=0,24
non non
à quoi correspondrait ton calcul ?
Avec T2=0,3 ---- faux
P1=0,5 ---- ceci est exact
tu as fait l'arbre des 2 premiers passages ?
coup de pouce
et révision de cours, si besoin ![]() Probabilités conditionnelles et indépendance
Probabilités conditionnelles et indépendance
non ce calcul est faux
étudie la fiche, au paragraphe probabilités totales.
(tu en auras aussi besoin à la question 1c)
p(T2) = p(T1  T2) + p(...?
T2) + p(...?  ...?) = ....?
...?) = ....?
bonjour MariamD
tes réponses de10h36 parfait !
1c) montre ton arbre pour voir (tu peux insérer la photo de l'arbre seul)
je t'aiderai à continuer.
cet arbre aide à répondre à la question 1b)
mais pas à la 1c)
==> pour 1c) on sort du cas particulier (du démarrage : passages 1 et 2),
et on raisonne pour un quelconque:
tes 2 branches de départ seront donc Tn et Pn...
ps : erreur de calcul sur ton arbre précédent, au niveau de la proba de P2 sachant T1
MariamD
je vais m'absenter pour le repas, mais je reviens ensuite lire tes réponses/questions.
bosse bien 
a+
J'ai refais l'arbre pondéré
Ensuite avec la formule des probabilités totales j'ai trouvé
p(Tn+1)=p(Tn Tn+1)+p(Pn
Tn+1)+p(Pn Tn+1)
Tn+1)
=0,3*Un+1-Un*0,2
=0,3Un+0,2-0,2Un
=0,1Un+0,2
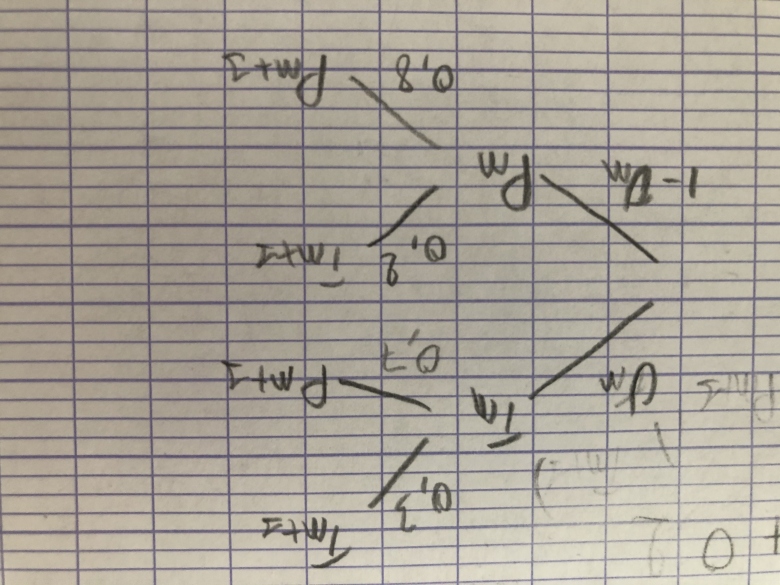
... p(Tn+1)=p(Tn
 Tn+1)+p(Pn
Tn+1)+p(Pn Tn+1)
Tn+1)
=0,3*Un+ (1-Un)*0,2 n'oublie pas les ( ) sinon c'est faux
=0,3Un+0,2-0,2Un
=0,1Un+0,2
pour la suite, tu as une idée ?
la suite (Un) : il s'agit d'une suite arithmético-géométrique, souvent vue dans les exercices;
peut-être en as-tu une en exemple dans le cours ?
le principe est toujours le même...
On sait qu'une suite géométrique est égale à Vn*q
Vn=Un-2/9  Un=Vn+2/9
Un=Vn+2/9
Vn+1=Un+1-2/9
=0,1Un+0,2-(2/9)
=0,1Un-1/45
=0,1(Vn+2/9)-1/45
=0,1Vn+0,1*2/9-(1/45)
=0,1Vn
=Vn*q
Donc (Vn) est une suite géométrique de raison q=0,1=1/10 .
Pour le b) j'ai fait --- non c'est en a) que tu dois préciser le 1er terme :
une suite géométrique se définit par sa raison q ET son premier terme.
V0=U0-2/9 --- attention U0 n'existe pas, et donc V0 non plus
=0,5*0,1 --- en rouge faux
Vn=V0*qn --- formule à adapter en fonction de l'indice du 1er terme (qui n'est pas 0)
reprends
pas vu ...
V1=U1-2/9
= T1-2/9 ah non T1 n'est pas correct : c'est un événement, pas un nombre ! U1 est sa proba, donc un nombre
d'accord ?

non, tu vas utiliser l'expression du terme général pour calculer la limite
Un=5/18*0,1^(n-1) + 2/9
lorsque n tend vers + , n-1 aussi.
, n-1 aussi.
0,1^(n-1) va tendre vers .....?
donc 5/18*0,1^(n-1) tend vers .....?
etc
pas de calculatrice
0,1^(n-1) va tendre vers .....?
==> regarde dans le cours, chapitre suite géométrique, la limite de q^n selon la valeur de q
lorsque 0 < q < 1 la limite de q^n tend vers 0
donc lorsque n tend vers + infini, (n-1) tend aussi vers + infini,
et 0.1^(n-1) tend vers 0
exemple :
0.1² = 0.01
0.1³ = 0.001
0.1^10 = 0.0000000001 ----> on rapproche de plus en plus vers 0 (par valeur positive)
ensuite
5/18 * 0,1^(n-1) va donc tendre vers ...?
et 5/18*0,1^(n-1) + 2/9 va tendre vers ...?
5/18*0,1^(n-1) tend vers -
5/18*0,1^(n-1) tend vers - car les de rapproche de 0 et sont de plus en plus petites.
car les de rapproche de 0 et sont de plus en plus petites.
oui
0,1^(n-1) tend vers 0
5/18 * 0,1^(n-1) tend vers 0
et donc 5/18*0,1^(n-1) + 2/9 tend vers ?
(compare ton résultat avec les premiers termes de la suite)

 =5/18*0,1
=5/18*0,1

