Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Exercice Ramanujan Term S
Posté par mousse42
Salut Ramanujan
Exercice
Soient et
et  deux fonctions continues sur un intervalle contenant
deux fonctions continues sur un intervalle contenant  et
et  , avec
, avec 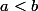
On pose![P(\lambda)=\int_a^b\big[\lambda f(t)+g(t)\big]^2dt\quad \lambda \in \R](https://latex.ilemaths.net/ile_TEX.cgi?P(\lambda)=\int_a^b\big[\lambda f(t)+g(t)\big]^2dt\quad \lambda \in \R)
1 Vérifier que est bien définie
est bien définie
2 Montrer que) est un trinôme de second degré au maximum. On montrera que
est un trinôme de second degré au maximum. On montrera que =A\lambda^2+B\lambda +C) où
où 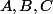 sont à déterminer.
sont à déterminer.
3 Que signifie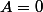 pour la fonction
pour la fonction 
4 On suppose que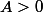 . Etablir l'inégalité de Cauchy-Schwarz
. Etablir l'inégalité de Cauchy-Schwarz ^2\le \left(\int_a^bf^2\right)\left(\int_a^bg^2\right))
Soient
On pose
1 Vérifier que
2 Montrer que
3 Que signifie
4 On suppose que



