Inscription / Connexion Nouveau Sujet
exercice sur fonctions
bonjour a tous voila cet exercice me pose problème car je ne vois pas quoi faire pour démontrer
A et B deux point d'un cercle centre O tels que (OA;OB) appartienent à 0;pi.
M est milieu de l'arc AB.
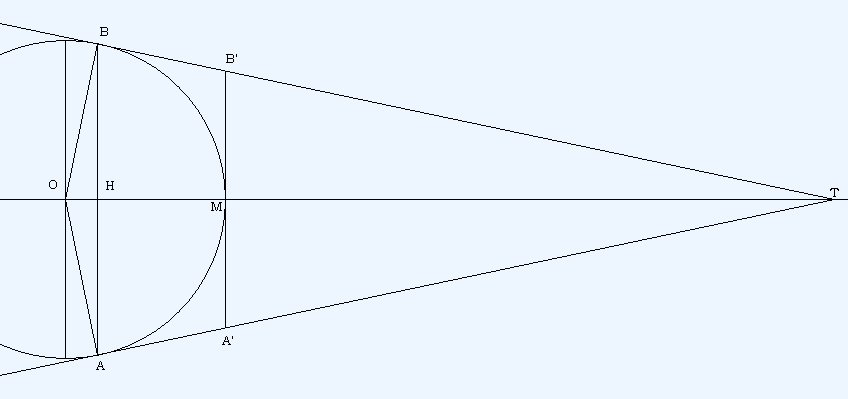
Les tangentes en A et B au cercle se coupent en T et la tangente à M coupe (TA) en A' et (TB) en B'.
Quelle est la limite de: (aire(A'TB')/(aire(ATB) (si elle existe) lorsque A tend vers B?
Merci de votre aide.
Avant de calculer la limite, calcule chacune des aires et le rapport en question. Ensuite seulement, tu te poseras la question de la limite de l'expression que tu auras trouvée.
Le minimum, c'est de faire la figure. Trace ton cercle, les points A,B,M, TA, TB, A', B', les tangentes, tout quoi !
Et réfléchis un peu ! Tu sais calculer l'aire d'un cercle ? D'une portion de cercle ? d'un triangle ? Tout cela date de la troisième, si ce n'est auparavant ! Tu as tout ce qu'il faut ! Fais un effort !
Seul le calcul de la limite demande les connaissances de la première !
Ben je te la donne la distance de base. Fais les calculs avec OA=R !
Maintenant tu as la distance OA, qui vaut R. Tout le reste s'ensuivra, et tu t'apercevras que R disparaît lorsque tu fais le rapport demandé. Voilà pourquoi on ne t'a pas donné OA : tu n'en as pas besoin ! Et pour faire les calculs, tu poses simplement OA=R !
J'ai le même problème mais je ne vois pas comment l'on peut se servir de OA pour arriver a trouver l'aire des triangles .
L'un et l'autre, faites un dessin !
Je pose , et OA=OB=R !
Est-ce qu'avec a, vous n'êtes pas capable de calculer la longueur de OT ?
Moi, je vois que OB/OT = cos(a) pas vous ? J'en déduis : OT=OB/cos(a)=R/cos(a)
Les aires des triangles demandés sont égales respectivement à : AB*HT/2 et A'B'*MT/2, non ?
Par ailleurs, j'ai cos(a)=OH/OB, d'où je tire aisément OH=OB cos(a)=R cos(a)
Donc on a OH, puis HT=OT-OH, puis MT=OT-OM=OT-R, etc...
Tout cela est du niveau seconde ! Quand vous serez arrivés à la formule donnant (aire(A'TB')/(aire(ATB)), où vous constaterez que, miraculeusement, R a disparu (donc, ce n'était pas si grave de ne pas connaître R !), alors là oui : il s'agira de trouver la limite de la formule et ça, c'est bien du niveau Terminale !
pour trouver AB, on cherche AH avec Pythagore que l'on multiplie par 2 ?, parce que je suis pas sur de l'utilité de Pythagore ici.
Pythagore va te donner des racines ! On parle de l'angle a, donc, il vaut mieux utiliser la trigonométrie ! AH=R * sin(a)
Pour moi, ce dessin est un cas particulier car moi j'ai fais plusieurs dessins et je ne trouve pas toujours que M T et O Sont alignés et je ne trouve pas non plus d'angle droit entre AB et OT !! (je ne vois pas comment je pourrais démontrer que HT est la hauteur du trinagle ABT)
Est ce que ce sont des erreurs de ma part ou votre dessin est vraiment un cas particulier ??
Est ce que ce sont des erreurs de ma part ou votre dessin est vraiment un cas particulier ??
Ce sont des erreurs de ta part, car mon dessin n'est pas un cas particulier !
Si l'on trace les tangentes en A et en B, elles se coupent en T. Alors
Alors
Le triangle ABT est donc isocèle.
Par ailleurs, si H est le projeté orthoglonal de B sur OT, on a OH=OB²/OT
et si H' est le projeté orthogonal de A sur OT, on a OH'=OA²/OT=OB²/OT=OH
Par conséquent H et H' sont confondus, la droite AB est perpendiculaire à OT.
Ensuite, on peut dire que HB*OT=OB*BT et que HA*OT=OA*AT=OB*BT=HB*OT. Donc HA=HB. Le point H est donc le milieu du segment AB.
Tout cela est quasi évident : on aurait pu dire dès le début, que pour raison de symétrie (la figure est symétrique par rapport à OT) il est évident que AB est perpendiculaire à OT. Mais j'ai détaillé pour toi !
Il est impossible de faire une figure parfaite ! Ne dit-on pas que la géométrie, c'est l'art de raisonner juste sur des figures fausses ? Ma figure je l'ai faite avec un ordinateur, donc elle est assez propre. Si tu fais ta figure à la main, à la règle et au compas, c'est très difficile de faire une figure parfaite, je comprends cela ! Mais même si elle est imparfaite, il faut savoir reconnaître certaines propriétés non visibles sur le dessin, par le raisonnement !
Bon courage !
Bonsoir,
J'ai le même sujet, cependant je bloque dans le développement est-ce que vous pourriez m'aidez ?
Je sais que TM = r/cosθ -r et A'B' = 2 tan(θ/2)*r
De plus TI = r/cosθ - r*cosθ et AB = 2sinθ*r
J'ai également trouvé une limite de 1/4 en conjecturant avec géogebra.
Merci
Le développement (aire(A'TB')/(aire(ATB)) je n'arrive pas à simplifier assez pour faire disparaître les indétermination, est-ce que je pars des bonne choses avec mes valeurs de TM, TI, A'B' et AB.
Sur la figure ci dessus H représente mon I
pour A'TB' j'ai (TM x A'B')/2 donc ((r/cosθ)-r) x 2r tan(θ/2))/2
en développant j'ai à la fin r^2 tan(θ/2) x (1/cosθ -1)
Pour ATB j'ai (TI x AB)/2 donc ((r/cosθ)-rcosθ) x 2r sinθ)/2
Notre inconnue, on ne connait pas non plus le rayon. Il faut réussir à développer pour obtenir une expression avec peu de  et sans "r".
et sans "r".
Je n'y arrive pas il y a toujours trop de  ce qui me donne des formes indéterminées pour la limite.
ce qui me donne des formes indéterminées pour la limite.


