Bonjour,
Et toujours merci pour l'animation..

 Cliquez pour afficher

je dirais 8/8/4
et  3/8/9

bonjour dpi et Sipok

En effet , il y a , en principe, 2 cas favorables pour 1 non favorable et tout événement certain a pour probabilité 1 et non pas 2/3 . Donc p(5/6/9; 8/8/4 etc...) = 1 mais pas 2/3

Bonsoir ming.
Je m'interroge sur sur le sens de ta question.
Déjà l'affirmation

Bonsoir verdurin
Dans la présentation, on choisit "au hasard" trois nombres et l'on sait qu'ils ne mesurent  pas toujours les côtés d'un triangle (non aplati) mais une fois sur quatre.
Qu'est-ce qui est douteux? Ce qui peut l'être, c'est la façon de choisir "au hasard" ces trois nombres. Par exemple, on peut demander à trois personnes de choisir chacune "au hasard" un nombre.
Ensuite,

Re dpi et Sipok

Vous pouvez oublier ma remarque...
Vos réponses n'étant pas justifiées, pouvez-vous m'éclairer?

Bonjour,

Tout d'abord pour un total de 20 pour 3 nombres  a,b,c  ,il y une liste acceptable.
Dans cette liste on élimine  les cas a<b+c   b<a+c   c <a+b.
Il ne reste que  8 candidats.
Un petit coup d'Al Kashi /Héron et on en trouve deux.
donc 2/8 sauf erreur.

bonjour verdurin

Effectivement, dans la présentation, il manquait la somme n des mesures des trois côtés a, b et c.
Donc , n est donné , on choisit au hasard a et b  tels que a + b < n.
La probabilité de l'évènement:  a, b et c  = n-(a+b) sont les mesures des côtés d'un triangle  non aplati est 1/4.
a, b et n sont réels strictement supérieurs à 0.

Je crois que la démonstration est due à Emile Lemoine; il utilise une propriété du triangle équilatéral: la somme des distance d'un point intérieur au triangle aux trois côtés égale la longueur de la hauteur.

Bonsoir ming.
Effectivement, j'aurai du y penser.
Mais je suis bêtement parti sur trois nombre tirés uniformément dans [0;1].
Ce qui donne une probabilité de 1/2 d'avoir un triangle.

Pour ta question j'ai trouvé deux solutions, mais elles sont vraiment inélégantes.

Je vais essayer de penser encore un peu avant de les poster.

Bonsoir.

Une possibilité.

 Cliquez pour afficher

On prend un segment de longueur 8 et on coupe en deux morceaux (la coupe étant faite suivant une loi uniforme) un segment de longueur 12.

bonsoir  verdurin

 Cliquez pour afficher

En effet; c'est la bonne réponse. Veux-tu l'exposer s' il te plait? j'indiquerai ensuite la mienne.

Bonsoir ming.
En fait j'ai interprété « tirer au hasard uniformément trois nombres dont la somme est 20 » par « choisir au hasard  uniformément et indépendamment deux nombres x et y entre 0 et 20 ».
En prenant a =min(x,y) et b=max(x,y) les nombres tirés pour les côtés sont a, b-a et 20-b.

On a alors un schéma mois symétrique que le triangle équilatéral, mais plus exploitable.

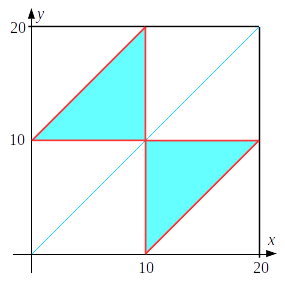
les points bleus ( et rouges ) correspondants aux cas où on peut avoir un triangle, éventuellement aplati.

 Cliquez pour afficher

Pour la solution que j'ai donné, j'ai recherché une valeur de x tel que a=x<10 et qui intercepte 2/3 de la zone bleue situé « au dessus » de la droite x=y.

Ma seconde solution s'en déduit  facilement : on tire x au hasard et uniformément entre 6 et 10, puis on tire y uniformément entre x et 20.

Ceci étant dit, j'espérais une solution en modifiant les densités de x et y.
Mais je suis certain ( ou presque ) que l'on ne peut pas obtenir une probabilité supérieure à 1/2 sans abandonner l'indépendance entre x et y.

merci verdurin , je vais regarder ta solution.
En attendant, en voici une.

 Cliquez pour afficher

Solution simple
a, b et c sont les mesures des côtés d'un triangle non aplati de périmètre 20, si et seulement  si, a<10, b<10 et c<10.
On peut prendre indifféremment l'une des valeur a ou b ou c pour commencer la construction du triangle. Considérons par exemple a.
On cherche les positions favorables de E sur un segments [XY] tel que :
XB= a, BE = b et EY = c, X, B, E et Y sont dans cet ordre.
Plaçons sur ce segment les points B, D et C tels que XB = a < 10 et 
BC = DY = 10.
Plaçons  maintenant E à la suite de B tel que BE = b.

Si E[BD] alors EY=c > 10 impossible
.
SI E [CY] alors BE = b > 10 impossible.
Donc E ]DC[.
Réciproquement, si l'on prend 
E]DC[, alors b=BE<BC=10 et c= EY<DY = 10.
Les positions favorables de E forment le segment ]DC[.
Toutes les positions possibles de E constituent le segment [BY].
La probabilité est donc DC/BY = a/(20-a).
On désire: a/(20-a) = 2/3 a = 8.
On obtient également 2<b<10 , 2<c<10 avec b+c =12.
En commençant par b ou c, la démonstration est identique (b = 8 ou c = 8)
Conclusion, l'un au moins des côtés doit mesurer 8.
Remarques:

On peut également démontrer le résultat en s'inspirant du mathématicien Emile Lemoine à l'aide d'un triangle équilatéral dans un plan ou dans³ en considérant un triangle équilatéral dans le plan x+y+z = 20.

Bonsoir ming.
Je crois que nos approches sont assez différentes.
Ce qui est bien c'est que l'on trouve le même résultat.

Sinon, une voie que je trouve plus satisfaisante.

La valeur du périmètre n'a aucune importance.  On peut donc prendre un périmètre égal à 1.
On le coupe en deux suivant une loi bêta dont les deux paramètres sont égaux à b (ce qui assure une symétrie des coupes).
On recoupe le morceau le plus long ( ce qui assure de façon simple la dépendance entre les deux coupes) suivant la même loi, via une proportionnalité à sa longueur.
Pour b=1 on trouve un résultat légèrement inférieur à 2/3 et pour b=2 un résultat supérieur à 2/3.

Il y a donc une valeur de b situé entre 1 et 2 qui donne le résultat voulu.

Mais j'ai beaucoup de mal avec le calcul numérique d'intégrales doubles. (Pour b=1 et b=2 le calcul exact est assez simple).

Je vais quand même réessayer, mais premières tentatives m'ayant conduit à des résultats aberrants.

mes premières tentatives m'ayant conduit à des résultats aberrants.

bonsoir verdurin

je ne connais pas la loi mais est-ce nécessaire?
De plus, j'ai passé l'âge des intégrales multiples mais je lirai volontiers ta démonstration car je trouve que tu as du mérite d'approfondir ce sujet: je n'ai pas la même curiosité.

Bonjour,

Pour ma part ,ma réponse ne se base que sur des Naturels et non des
Réels.
Il y a 2 triplets sur 8 possibles ce qui simplifiait grandement le problème

dpi

Oui mais ce serait trop facile.

Bonsoir.
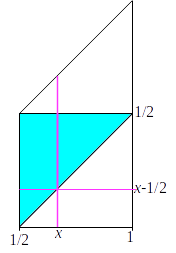
Pour le schéma de départ

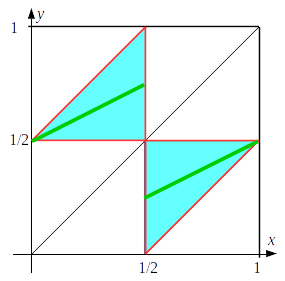
En prenant le cas les segments mesurent .
On écrit les inégalités triangulaires :



Ce qui donne le triangle bleu en bas et à droite.
L'autre triangle est obtenu par symétrie, en supposant .

Ensuite
L'idée de base est que si on recoupe au milieu le plus grand morceau obtenu après le premier partage, on peut toujours faire un triangle.
On est sur les lignes vertes du schéma ci-dessus.

Il convient donc, pour augmenter la probabilité d'avoir un triangle, de recouper le plus grand morceau aux alentours du milieu.

Pour des raisons esthétiques, j'ai décidé que les lois de de partages du premier segment et du morceau le plus long après le premier partages devaient être identiques ( à un facteur d'échelle près ) et à densités continues et symétriques.

J'ai donc regardé des densités proportionnelles   à un facteur d'échelle près pour la seconde coupe.
C'est à dire que la variable aléatoire X donnant la position de la première coupe suit une loi bêta de paramètres b+1 et b+1, et que, si x est la longueur du plus grand morceau, la variable aléatoire Y donnant la position de la seconde coupe est telle que Y/x suit une loi bêta de paramètres b+1 et b+1.
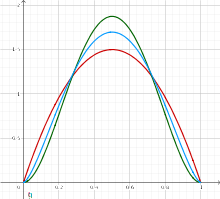
Une image pour les densités correspondants à b=1, b=2.5 et b=3. Quand b augmente, la densité se concentre vers le milieu du segment.




Le calcul
En utilisant la symétrie entre x et 1-x, on peut supposer Ce qui entraîne que le résultat obtenu doit être multiplié par 2.

On voit sur le dessin ci-dessus que, X=x étant donné, on a un triangle quand Y est entre x-1/2 et 1/2.
Et donc Y/x entre 1-1/(2x) et 1/(2x).

En désignant par f la densité commune de Y/x et de X on a donc



puis

.

Il est évident que la probabilité d'avoir un triangle est une fonction croissante de b.

J'ai fait du calcul numérique avec XCas, quand j'ai réalisé que la loi bêta faisait certainement partie de son répertoire.
g désignant la fonction qui associe à un exposant b la probabilité g(b) d'avoir un triangle quand X et Y/x suivent la loi bêta de paramètres b et b on a :

g(b):=2*nInt(betad(b,b,x)*betad_cdf(b,b,1-0.5/x,0.5/x),x,0.5,1)

bonjour verdurin
Excuses mais je n'ai pas pu te lire jusqu'au bout...
Je n'ai plus le niveau suffisant (ni l'envie) de  comprendre cette théorie.
(l'Envie est un restaurant à côté de Toulon : cet envie me tente plussss)

Comme je te comprend !
Mais ma douce et tendre préfère ma cuisine à celle des restaurants.

bonjour  verdurin

Tu te fais exploiter...Alors que fait-elle pendant que tu es aux fourneaux?

Elle n'est pas encore à la retraite : elle travaille.