Inscription / Connexion Nouveau Sujet
Extrémum géométrique
Bonjour,
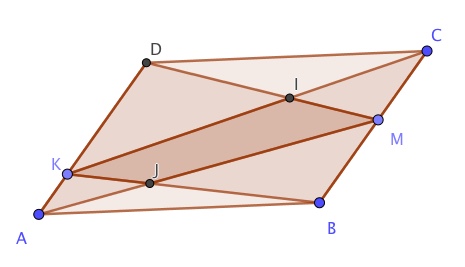
Je cherche à résoudre le problème suivant. Pourriez-vous m'aider SVP ? Soit ABCD un parallélogramme ; K un point sur [AD] et M un point sur [BC]. Il faut montrer que l'aire du quadrilatère KIMJ obtenu à l'"intersection" de AMD et BCK (voir figure ci-dessous) est maximale quand AK = MB. Pour l'instant, la seule chose que j'ai trouvé, c'est que pour AK = MB, l'aire de ce quadrilatère KIMJ est le quart de l'aire de ABCD ; j'ai découpé ABCD en ABMK et KMCD ; et sachant que ce sont aussi des parallélogrammes dans ce cas (c'est-à-dire quand AK = MD), ça m'a donné l'aire de ce quadrilatère KIMJ. En revanche, je ne vois pas comment montrer que lorsque , on n'atteint pas cette borne.
Bonjour g0217d.
De quelles méthodes avez-vous le droit de disposer pour résoudre cet exercice ?
Si vous avez le droit à des méthodes analytique, alors je me placerais dans le repère et commencerais à poser des coordonnées, calculer des équations de droites, des intégrales, et notamment, l'aire cherchée = Aire(AKIMB) - Aire(AKB)
Bonjour,
Cela revient à montrer que la somme des aires des triangles extérieurs au quadrilatère est minimale. La position de K et celle de M sont deux variables. Il va donc y avoir probablement une question de minimum d'une fonction de deux variables.
Je serais tenté de me ramener au cas du rectangle (une déformation simple ne change rien au problème), voire même au carré de côté 1, et d'écrire les calculs en repère orthonormé.
bonjour,
Dans l'attente d'une solution moins calculatoire et en s'appuyant sur les méthodes préconisées ci-dessus, on peut définir le maximum en calculant la somme des produits vectoriels:
je fais disparaître le coeff 1/2 (1/2)[aire de (KJM)+aire (KMJ)]
Si on pose Km=k et BM=m, d'après le texte le paramètre s=k+m semble indifférent avec cependant et on pose
; par symétrie on peut supposer
et donc d=m-k
On exprime la somme précédente en fonction de s et de d.
Je n'ai pas effectuer les calculs jusqu'au bout mais il me semble, sauf erreur, que l'on fera intervenir une fonction f du second degré en d, avec
sur l'intervalle [0,1] et dont les coefficients dépendent de s .Tout cela est à vérifier.
Bon je crois qu'en fait c'est tout bête :
Comme les droites (BC) et (AD) sont parallèles, l'aire du triangle BKC ne dépend pas du point K sur la droite (AD), car la hauteur du triangle est toujours constante.
On en déduit que les aires des triangles BKC et AMD sont identiques puisque le quadrilatère ABCD est un parallélogramme (car hauteurs et bases identiques pour les deux triangles)
Reste juste à voir pourquoi l'aire de superposition est maximale quand K et M sont au centre de leurs segments respectifs.
bonjour jsvdb,
Il me semble que le pb est posé quand AK=MD et non pas quand K et M sont les milieux respectifs de [AD} et de [BC].
Il n'est pas demandé l'aire maximale pour toutes les positions de K et de M
Bonjour,
pas d'accord
le problème est bien posé pour AK et MB quelconques indépendants et il faut prouver que l'aire est maximale lorsque AK = MB (= une valeur quelconque)
Je prends A = (0,0) , B = (1,0) , C = (1,1) , D = (0,1) , K = (0 , s) , M = (1,t) où s , t sont dans ]0 , 1[ .
Soient U(s,t) l'aire de AJK , V(s,t) celle de KID et W(s,t) celle de KJMI
Comme U + V + W = 1/2 on va étudier les variations de U + V pour avoir celles de W
Si je ne me suis pas trompé dans les calculs on obtient que l'abscisse de J est s/(s + t) et celle de I est (1 - s)/(2 - s - t) donc
2U(s,t) = s²/(s + t) et 2V(s,t) = (1 - s)²/(2 - s - t) .
..s étant fixé la dérivée de t  s²/(s + t) + (1 - s)²/(2 - s - t) a le signe de t - s ce qui permet de voir que Sup(W(s,.) = W(s,s) .
s²/(s + t) + (1 - s)²/(2 - s - t) a le signe de t - s ce qui permet de voir que Sup(W(s,.) = W(s,s) .
______
Pour voir qu'on peut se ramener au cas où ABCD est un carré on utilise ce qu'on appelait autrefois les "affinités " .
Merci beaucoup pour vos réponses. Ça m'a permis de trouver finalement. En gros, j'obtiens les mêmes résultats que toi etniopal, sauf que je suis resté sur un parallélogramme. La fonction à étudier dans ce cas est
avec x = AK, y = BM, a = AD et h = distance de A à (BC).
D'ailleurs, merci etniopal pour ton astuce de fixer un paramètre (y dans mon cas) car avec le théorème de Monge j'obtenais
bonjour,
les démonstrations précedentes sont astucieuses
avec ma proposition il me fallait déterminer la valeur de d=BM-AK pour que -d²-2sd+4s soit maximum s étant AK+BM, il est clair que d=0


 géométrie en post-bac
géométrie en post-bac