bonjour : )

Il s'agit essentiellement de savoir lire ton tableau de variations.
Tu peux aussi essayer de tracer le graphe de .

salut,
tu as certainement une defintion pour fonction minoree sur un intervalle ?

Merci

f est minorée sur I si, x I , il existe un réel m tel que:

m f(x)

f est croissante sur ]-1, 0[U ]3,+[

et décroissante sur ]-, -1[U]0, 3[

Ta définition n'est pas exacte, il est important que tu saches écrire correctement une définition, pas à ta manière.

Ensuite, à nouveau, il s'agit essentiellement de savoir lire ton tableau de variations.

Un dessin rapide te permet de visualiser un minorant possible si jamais le tableau de variations n'est pas clair pour toi.

mes eleves ont le droit d'ecrire:
d'apres le tableau des variations on a:
pour tout x de l'intervalle ]-inf;-1], f(x)>=-4
donc f est minoree par etc

Bonjour

Citation :
et majorée sur ]-1, +[.

salut

beugg @ 13-08-2016 à 15:33

Merci

f est minorée sur I si, x I , il existe un réel m tel que:

m f(x)

f est croissante sur ]-1, 0[U ]3,+[

et décroissante sur ]-, -1[U]0, 3[

"une fonction n'est jamais (dé)croissante sur une union d'intervalles"
Pourquoi ?

DEF : la fonction f est décroissante sur l'intervalle I si pour tous u et v de I :

prenons la fonction inverse f(x) = 1/x

elle est décroissante sur ]-oo, 0[ et (sur) ]0, +oo[

elle ne l'est évidemment pas sur leur union puisque -1 = f(-1) < f(1) = 1

tu m'as dejà fait le coup dans un autre fil
je parle de la definition qu'on voit apres le bac

une fonction peut-etre monotone sur une reunion d'intervalles disjoints

1/ oui mais là on est en première ...

2/  la fonction f(x) = x sur [1, 2] [3,, 4] est bien "croissante sur l'union" (si tu veux ... par abus de langage)

mais la fonction g(x) =
-x + 10 sur [1, 2]
-x sur [3, 4]

n'est pas décroissante sur l'union alors qu'elle l'est sur chacun des intervalles

on est bien d'accord
au lycee on se restreindra aux intervalles pour la monotonie
mais celle-ci se definit en general pour des applications de E vers F
E et F etant simplement ordonnes

Ok, merci

malou @ 13-08-2016 à 16:32

Bonjour
tu es sûr de cet énoncé ?....de ce +   ?

oui
pour tout x de l'intervalle ]-inf;-1], f(x)>=-4
donc f est minoree par -4 sur l'intervalle  ]-inf;-1]

Ok

Donc est-ce qu'on peut dire sur ]-1, +00[ f est majorée ?

sur [-1;inf[ tu ne peux rien dire
il manque probablement dans ton tableau la limite en plus l'infini

-4 et 0 sont des minimums ; 1 est un maximum

Bref

f est majorée sur ]-1, 0]

2/

f est bornée sur ]-1, 3[ car 0 f(x) 1?

il existe un réel m tel que pour tout x de I, mf(x)

toi tu avais interverti le "il existe m" et le "pour tout x" et donc ton m pourrait dépendre du x quelconque que tu choisis ensuite
l'ordre a grande importance dans l'énoncé de ces définitions
et l'usage des quantificateurs ne facilite pas la compréhension des choses

Oui tout à fait,vous avez raison !

f(x) n'est pas compris entre 0 et 1

Si la fonction est à la fois majorée et minorée , f est bornée ?

oui

Donc f est bornée par 0 et 1 sur l'intervalle]-1, 3[ ?

remonte à 14h18

Donc je ne comprends pas bien

Merci de m'expliquer

quelle est la plus petite valeur prise par f(x) sur cet intervalle ?  et la plus grande ?

Désolé

f est bornée par -4 et 0 sur cet intervalle

ça peut pas "monter" au dessus de 0 ?

Pardon toujours

C'est plutôt -4 et 1

Je suis désolé !![url][/url]

Je ne réponds pas au hasard mais c'est une male compréhension !

C'est peut-être je ne sais pas lire correctement mon tableau de variation!

la valeur la plus "basse" sur cet intervalle est ??
la valeur la plus "haute" est ??

les valeurs lues dans le tableau te permettent de dire que ta fonction est bornée sur ton intervalle

malou edit > pour ne pas laisser des erreurs sur le fil

Mais sur mon intervalle 1 est le maximum pourquoi 4  ? -1 non plus ?

c'est bien -4 et 1 effectivement

le temps de scroller en bas de la page, j'avais interverti les signes.... excuses !

Non pas de problème,merci beaucoup à vous tous

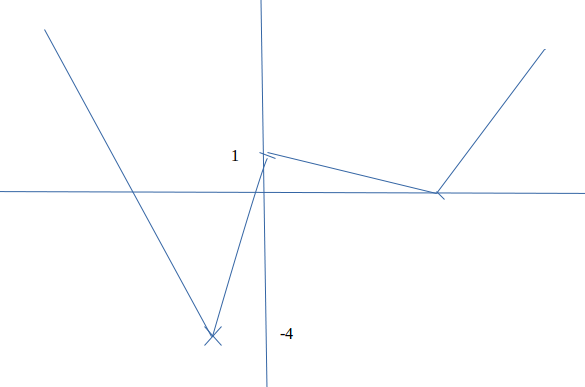
qd tu as ce genre d'exo, faire un croquis d'une courbe possible dès le début est pas mal...
on y voit bien que sur l'intervalle qui t'intéresse, -4 est le mini, et 1 est le maxi
(sur un papier au brouillon, ça va mieux qu'à l'ordi !)

Ok! Merci malou