Inscription / Connexion Nouveau Sujet
Fonction égale à sa réciproque
Bonjour,
Pour info, ce n'est pas un exercice de cours mais une interrogation personnelle.
Je me demandais simplement comment trouver l'ensemble des fonctions qui vérifient f=f-1 (réciproque de f).
Travaillons, au moins dans un premier temps, sur les fonctions de U
à valeurs réelles
Je sais simplement que la fonction inverse vérifie cette propriété sur leur ensemble de définition (*) et l'identité aussi sur .
Y a-t-il une méthode ?
Merci
Bonsoir
On peut considérer une partition de R en deux parties E et F de même cardinal et une bijection b de E dans F .
La bijection qui associe b(x) à tout x de E et b-1(x) à tout x de F vérifie les conditions .
Imod
y = f(x) 
f-1(y) = x f(y) = x.
Si (x,y) appartient à la courbe de la fonction alors (y,x) aussi.
Ces fonctions sont donc symétriques par rapport à la droite y=x.
Bonsoir à vous deux.
Pour Imod, je comprends bien le mode de construction des bijections.
Pour little fox aussi.
Cependant, je voulais savoir s'il est possible d'exhiber les solutions, ou du moins certaines d'entre elles. On voit facilement que l'identité et la fonction inverse sont symétriques, et aussi, du coup, les restrictions à ces fonctions sur quelconques intervalles I
Mais comment trouver l'ensemble des fonctions réelles symétriques par rapport à la droite x=y ?
On peut donner facilement un mode de construction de toutes les fonctions que tu cherches . On choisit au hasard un ensemble de points fixes F . Si le complémentaire de F est infini ou de cardinal pair on le partitionne en deux parties G et H de même cardinal et on considère une bijection g de G dans H
On définit alors f de la façon suivante :
f(x)=x si x est dans F
f(x)=g(x) si x est dans G
f(x)=y où y est l'unique élément de G tel que g(y)=x si x est dans H.
Clairement fof=Id et toute autre solution est de cette forme .
Imod
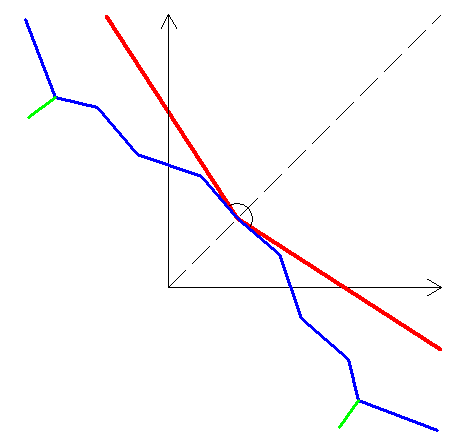
Un exemple d'une telle fonction :
Evidemment si tu veux la continuité sur R il risque d'être difficile d'échapper à Id et -Id . Sur un intervalle ça reste à voir , il y a au moins 1/x et -1/x .
Imod
Il y a pleins de fonctions possibles. Trouver une forme générale me semble impossible.
Tu as par exemple la famille f(x) = (a-xb)1/b avec le domaine [0,a1/b] si b n'est pas impair.
En particulier le quart de cercle avec pour centre l'origine : f(x) = 
(a-x2)
Et les droite perpendiculaires à y=x : f(x)=a-x.
Toutes les fonctions telles que f(f(x)) = x sont valides. Elles ne sont pas obligées d'être croissante, décroissante ou même continue.
On peut créer ces fonctions à partir de beaucoup de fonctions en prenant une partie du domaine et en utilisant la symétrique de cette partie. Par exemple :
Pour trouver cette symétrique il "suffit" de poser x = f(y) et de résoudre pour y.
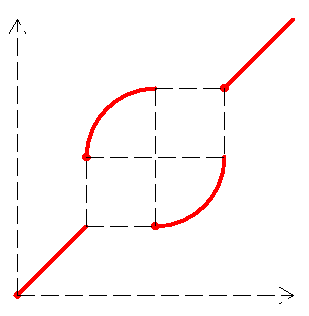
Oui , en fait il y a plein de solutions continues sur R 
On peut mettre à la place des deux demi-droites en rouge n'importe quelle fonction située du bon côté et ne traversant jamais ces demi-droites .
Imod
Pourquoi cet angle là? J'aurais plutôt vu des demi droites horizontales et verticales.
Je dirais même que l'image de tout point de la fonction doit être unique donc même par morceau la dérivée ne peut jamais changer de signe en un point continu.
J'avais choisi un angle complètement au hasard , j'essayais de me convaincre qu'il existait plein de solutions non convexes . En fait la stricte monotonie est obligatoire dès qu'on impose la continuité de la bijection . Je n'avais pas cherché à caractériser les involutions continues sur R mais en fait c'est simple .
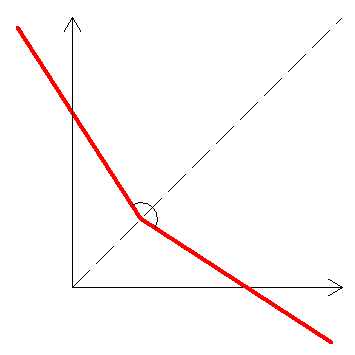
On va supposer la fonction f strictement décroissante sur R . Elle coupe la bissectrice y=x en un seul point (a,a) et la connaissance de f sur à gauche de a permet de la connaître à droite . Donc toute fonction strictement décroissante pour les valeurs inférieures à a et telle que f(a)=a va fournir une solution unique .
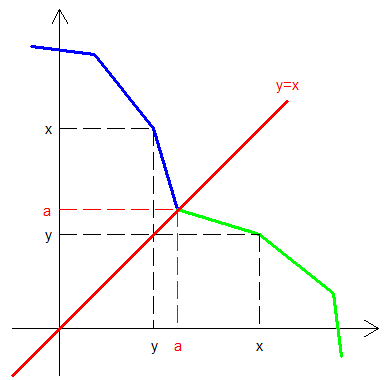
Le cas où f est strictement croissante doit se résoudre de la même façon ( je n'ai pas vérifié ) .
Imod
Bonsoir,
J'aime bien l'exemple du 06 à11h37 avec les quarts de cercle 
Pour ce qui est d'une fonction continue croissante, à part l'identité je ne vois pas trop 
En effet les solutions croissantes manquent d'imagination 
Bon , on a toutes les solutions continues sur R , il va falloir que Maxmaths paye sa galette
Imod
Bonjour
Je vais rajouter mon petit grain de sel théorique.
Travaillons directement sur les fonction de dans
.
Une fonction est donc dans ce cas la donnée d'un triplet où
est un graphe fonctionnel inclus dans
.
Autrement dit et
où
est le domaine de la fonction, c'est-à-dire l'ensemble des réels qui ont une image.
Pour répondre à la question de maxmaths65, les fonctions qui vérifieront seront donc les fonctions définies sur une partie de
et telles que leur graphe est symétrique.
Autrement dit, si est le graphe de
et
celui de
, on aura
Mais comme , les fonctions qui répondent à la question sont (sans autres hypothèses supplémentaires) toutes celles dont le graphique(*) est symétrique par rapport à la droite
.
Donc tout graphe fonctionnel G2 qui vérifie G = G-1 définit une fonction égale à sa réciproque.
Partant, l'imagination est sans limite.
________________________
(*) je n'ose pas parler de courbe.
Bonjour,
Un petit exemple inspiré de celui d'Imod avec les quarts de cercle :
f(x) = x + (-1)E(x)
On y voit, comme dans l'exemple d'Imod, que la fonction peut être croissante sur certains intervalles où elle vérifie f(x)
x .
Bonjour,
Un petit exemple inspiré de celui d'Imod avec les quarts de cercle :
f(x) = x + (-1)E(x)
On y voit, comme dans l'exemple d'Imod, que la fonction peut être croissante sur certains intervalles où elle vérifie f(x)
x .Pas mal comme exemple
Du coup ça contredit la conclusion de ta démo le 07-01-19 à 18:49. Pourtant toutes les étapes sont justes. Simplement a et b ne peuvent pas être aussi proches que l'on veut et rien n'empêche la fonction d'être croissante entre a et b avant de redescendre.
Par contre mon argument que la dérivée ne peut pas changer de signe sur une partie continue de la fonction tient toujours, non?
Du coup, pas de fonction croissante continue sur
autre que l'identité?Du coup, pas de fonction croissante continue sur
autre que l'identité?Obligatoirement non
Sinon, comment le point (a;f(a)) avec, par exemple a < f(a) irait "rejoindre" le point (f(a);a) sans que la fonction décroisse à un moment donné ?
Du coup ça contredit la conclusion de ta démo le 07-01-19 à 18:49
" f n'est pas croissante " : sur quel intervalle ?
Du coup, pas de fonction croissante continue sur
autre que l'identité?
D'accord, ce n'est pas possible pour une fonction croissante partout sur . Mais est-ce que ce serait possible une fonction continue sur qui soit croissante par endroit (et décroissante à d'autres)? Je pense que non.
On la fonction f(x) = -1/x qui est continue presque partout sur et qui est croissante partout
(c'est pas bon mais presque ^^)
@LittleFox : effectivement c'est pas possible d'envisager une fonction continue avec ne serait-ce qu'une partie croissante sur un intervalle.
En effet, si f est croissante, disons sur , alors f est croissante sur
.
Et dans ce cas, la fonction ne peut plus se permettre de décroitre sur [b;c] sous peine d'être également décroissante sur [f(c);f(b)] et f aurait alors des images en double sur [f(c);f(b)]. La continuité dans ce cas n'est plus valide.
Une autre démonstration, que je trouve plus simple, pour l'unique fonction croissante sur vérifiant f = f-1 :
Soit f = f-1 et f croissante sur ,
Si f(x) > x alors f(f(x)) 
f(x) ; donc x f(x). Contradiction.
Idem si f(x) < x .
Donc, pour tout x réel f(x) = x
Bonjour,
Un sentiment d'insatisfaction m'était resté pour la question des fonctions continues sur .
En remontant le fil, je me suis aperçue qu'Imod avait apporté une réponse le 7 à 17h52 :
En fait la stricte monotonie est obligatoire dès qu'on impose la continuité de la bijection
Si la fonction f est continue sur
et bijective alors f est soit strictement croissante sur , soit stictement décroissante sur .
Dans le second cas, elle n'est croissante sur aucun intervalle.
Dans le premier cas, si de plus f = f-1 alors pour tout x réel f(x) = x .
Oui , les solutions continues sur sont très faciles à caractériser .
L'identité est la seule solution strictement croissante . Si est strictement décroissante elle va couper la droite
en un point
unique . La connaissance de
dans un demi-plan de frontière
donne l'ensemble du graphe de
.
Réciproquement à quelle condition la donnée d'un point et d'une fonction
continue strictement décroissante sur
telle que
fournit-elle une solution continue sur
tout entier?
Il faut et il suffit que ne soit pas majorée sur
.
Imod
Annuler
connectez vous