Inscription / Connexion Nouveau Sujet
fonction, surjective, injective
Bonjour tout le monde
J'aimerais un peu d'aide pour corriger mon exercice
Soit f:
la fonction définie lorsque cela est possible par f(x)= x-2
x+1
1) Déterminer l'ensemble de définition D de f et montrer que f est continue sur D et montrer que f est continue sur D
2) Justifier que f est dérivable sur D*=D\{0} et determiner f'
3) f est elle dérivable en 0 ?
4) Etudier les variation de f et en déduire Im(f). F est elle surjective? Injective ?
5) Simplifier pour x
[0,1], ]f rond f(x). Que peut on en déduire ?
NB: seul le x est sous la racine
Où j'en suis ?
1) La fonction existe que si -2x>0 donc Df[0;+
Par contre je ne sais pas comment prouver qu'elle est continue
2) f est donc dérivable comme composé sur [0;+
de plus on a f'(x)= (x-2x+1)'
=1-2(1/(2x))
3) Non car on ne peut pas diviser par 0
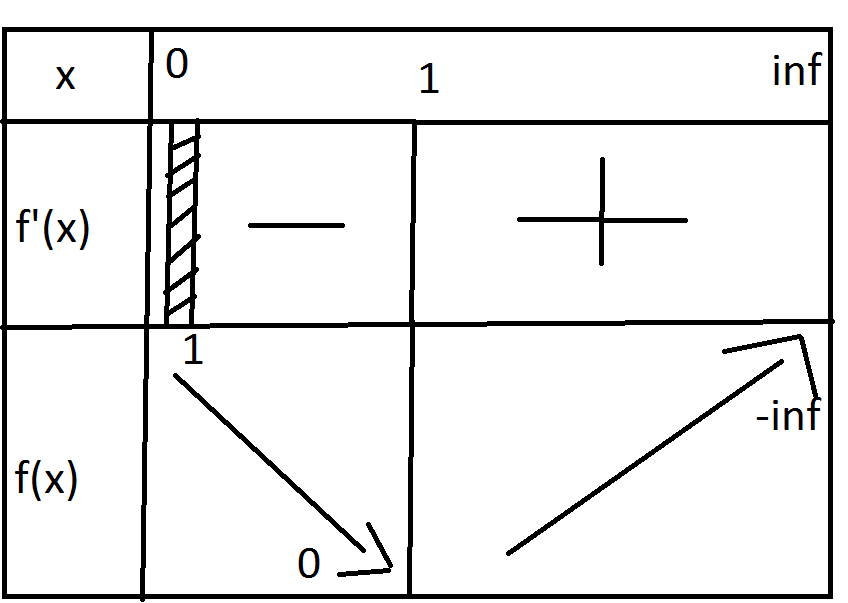
4) tableau de variation joint en photo
f est surjective sur Df mais pas injective
5) Je ne comprends pas cette question
Merci pour votre futur aide
Salut,
Pour la 3, ce n'est pas un argument, ou alors je ne vois pas le lien direct entre le fait qu'on ne puisse pas diviser par zéro et la non-dérivabilité.
Il faut former le taux d'accroissement et calculer sa limite :
donc n'est pas dérivable en
. Elle l'est par contre sur
par es théorèmes généraux.
Je n'ai pas compris votre justification sur la 3)
J'ai oublié de joindre l'image du tableau pour la 4) il se trouve sur cette réponse
Pour la 3), c'est la définition du taux d'accroissement.
Je calcule sa limite en car tu travailles sur
Pour ton tableau, ce n'est pas , mais
...
Euh oui je sais pas pourquoi j'ai mis -
en ce qui concerne la 3) j'essaie de la faire et vous donne le resultat quand j'ai finis
C'est d'usage sur un forum, et plus sympa 
D'accord comme tu veux 
Cela n'est pas valable pour notre fonction ?
En ce qui concerne la 1) je n'arrive toujours pas à montrer que la fonction est continue
Reste la surjectivité.
Tu as , donc l'image de
est égale à son ensemble d'arrivée, qui est
, d'où
surjective sur
Pour l'injectivité on le voit par le tableau de variation on passe de 1 a 0 puis de 0 à +inf donc on repasse forcement par l'intervalle [0;1] et donc deux antécédents sur certain éléments donc elle ne peut pas être injective
Pour la surjectivité on a d'après le tableau de variation
on a au moins un antécédents sur chaque éléments
Annuler
connectez vous
analyse en post-bac